Landen
Storyboard 
Der Schlüssel zur Landung besteht darin, den Flügel so zu modifizieren, dass ausreichender Auftrieb bei geringeren Geschwindigkeiten erzeugt wird, um eine kontrollierte Landung auf der Landebahn zu ermöglichen und das Flugzeug auf der verfügbaren Landebahn zum Stillstand zu bringen.
ID:(1968, 0)
Landen
Storyboard 
Der Schlüssel zur Landung besteht darin, den Flügel so zu modifizieren, dass ausreichender Auftrieb bei geringeren Geschwindigkeiten erzeugt wird, um eine kontrollierte Landung auf der Landebahn zu ermöglichen und das Flugzeug auf der verfügbaren Landebahn zum Stillstand zu bringen.
Variablen
Berechnungen
Berechnungen
Gleichungen
hnlich wie die Gleichung f r die Auftriebskraft ($F_L$) unter Verwendung von die Dichte ($\rho$), der Koeffizient Fahrstuhl ($C_L$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Geschwindigkeit in Bezug auf das Medium ($v$) abgeleitet wurde
entspricht in dieser Analogie das, was die Oberfläche, die Auftrieb erzeugt ($S_w$) entspricht, der Gesamtobjektprofil ($S_p$) und der Koeffizient Fahrstuhl ($C_L$) entspricht der Widerstandskoeffizient ($C_W$), woraus die Widerstandskraft ($F_W$) berechnet wird:
Der Widerstandsbeiwert wird gemessen und bei turbulenten Str mungen ber aerodynamischen K rpern werden blicherweise Werte um 0,4 ermittelt.
Wenn wir die Antriebskraft ($F_p$) mit die Widerstandskraft ($F_W$) mit der Gesamtobjektprofil ($S_p$), der Widerstandskoeffizient ($C_W$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) in
gleichsetzen, erhalten wir f r eine die Maximale Geschwindigkeit ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
was, wenn man es f r die maximale Geschwindigkeit l st, zu
f hrt.
Mit der Gleichung f r die Geschwindigkeit in Bezug auf das Medium ($v$) in der Startzeit ($t$) mit die Maximale Beschleunigung ($a_p$) und die Maximale Geschwindigkeit ($v_p$):
kann sie von einem Anfangswert von die Landegeschwindigkeit ($v_L$) aus integriert werden
$\displaystyle\int_{v_L}^v \displaystyle\frac{dv}{1 - v^2/v_p^2} = -\displaystyle\int_0^t dt a_p$
und mit der Definition von der Start-/Landeantriebszeit ($\tau_p$)
ergibt sich
Mit der Gleichung ERROR:6110,0 unter Verwendung von die Landegeschwindigkeit ($v_L$), die Maximale Geschwindigkeit ($v_p$), der Start-/Landeantriebszeit ($\tau_p$) und der Startzeit ($t$) wie folgt:
wobei in der Startzeit ($t$) gleich der Landezeit ($t_L$) ist, haben wir:
$v = v_L - v_p \tan\left(\displaystyle\frac{t_L}{\tau_p}\right)=0$
Wenn wir diese Gleichung nach der Zeit l sen, erhalten wir:
Da die Geschwindigkeit in Bezug auf das Medium ($v$) w hrend der Landung in Abh ngigkeit von der Startzeit ($t$) mit die Landegeschwindigkeit ($v_L$), die Maximale Geschwindigkeit ($v_p$) und der Start-/Landeantriebszeit ($\tau_p$) gem der folgenden Gleichung variiert:
ist es gleich der Zurückgelegter Weg auf der Piste ($s$) als Funktion von der Startzeit ($t$).
Wir k nnen die Gleichung integrieren:
$\displaystyle\frac{ds}{dt}=v_0-v_p\tan\left(\displaystyle\frac{t}{\tau_p}\right)$
und den Pfad erhalten als:
$s = v_L t + \log(|\cos( t / \tau_p)|) v_p \tau_p$
Wenn der Startzeit ($t$), kann der logarithmische Faktor bis zur dritten Potenz entwickelt werden, was dazu f hrt, dass der Landepfad gleich ist:
Beispiele
Flugzeuge verwenden drei Mechanismen zum Bremsen w hrend der Landung:
• Schubumkehr, bei dem der Triebwerksschub nach vorne umgeleitet wird anstatt nach hinten.
• Tragfl chenspoiler, die den Luftwiderstandsbeiwert erh hen, indem sie eine Fl che dem Luftstrom aussetzen.
• Konventionelle Radbremsen.
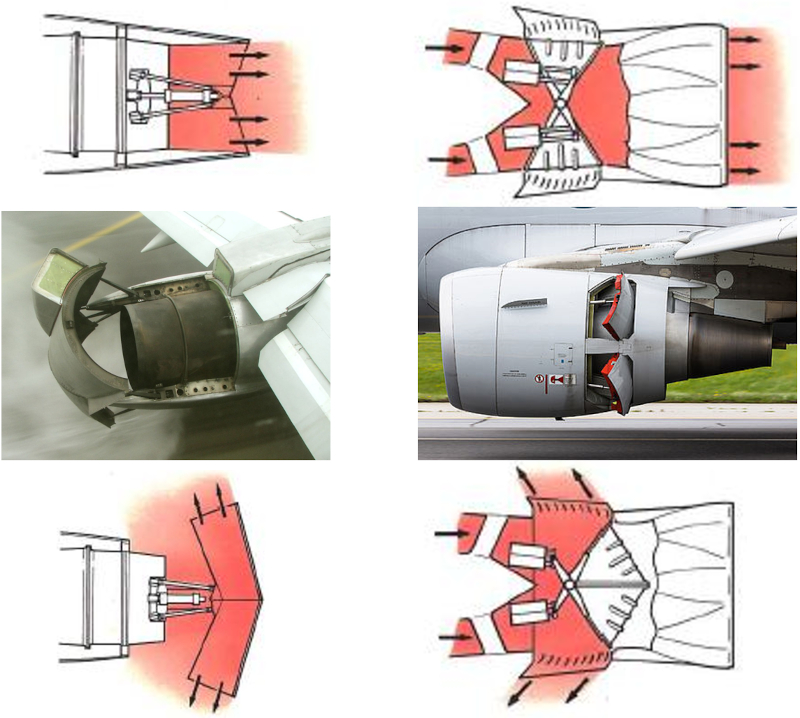
Das untenstehende Bild zeigt zwei Arten von Schubumkehr: Bei der ersten wird ein Umleiter in den ausstr menden Luftstrom des Triebwerks bewegt, w hrend bei der zweiten der Luftstrom direkt nach vorne umgeleitet wird.
Die Widerstandskraft ($F_W$) se puede utilizar con die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) y die Geschwindigkeit in Bezug auf das Medium ($v$) de acuerdo con la siguiente f rmula:
Zu Beginn des Starts ist der aerodynamische Widerstand, der von der Geschwindigkeit abh ngt, minimal. Daher wird die Maximale Beschleunigung ($a_p$) ausschlie lich durch die Antriebskraft ($F_p$) und die Körpermasse ($m$) bestimmt:
Da der aerodynamische Widerstand beginnt, die Schubkraft zu reduzieren, wird diese anf ngliche Beschleunigung maximal sein.
Die Antriebskraft ($F_p$) wirkt die Widerstandskraft ($F_W$) entgegen, indem es Geschwindigkeit erzeugt, was wiederum die gleiche Widerstandskraft erh ht, wie in der Gesamtobjektprofil ($S_p$), der Widerstandskoeffizient ($C_W$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) in
Dieser Prozess setzt sich fort, bis der Antriebskraft die Widerstandskraft entspricht, was die maximale erreichbare Geschwindigkeit darstellt.
Indem wir die Antriebskraft mit der Widerstandskraft gleichsetzen und nach der Geschwindigkeit l sen, erhalten wir die Maximale Geschwindigkeit ($v_p$):
Da der aerodynamische Widerstand beginnt, die Antriebskraft zu reduzieren, wird diese anf ngliche Beschleunigung maximal sein.
Mithilfe der Beschleunigung, die von den Triebwerken erzeugt wird und in der Formel
ausgedr ckt wird, sowie der maximalen Geschwindigkeit, die mit dem Luftwiderstand verbunden ist und durch
beschrieben wird, k nnen wir eine charakteristische Zeit definieren, die sich wie folgt ergibt:
Diese Zeit gibt eine Absch tzung der Gr enordnung des Start- und Landevorgangs, der in der Regel innerhalb von wenigen Minuten stattfindet.
Die Gleichung zur Berechnung von die Geschwindigkeit in Bezug auf das Medium ($v$) in der Startzeit ($t$) mit die Maximale Beschleunigung ($a_p$) und die Maximale Geschwindigkeit ($v_p$) lautet wie folgt:
Nach der Integration ergibt sich der Start-/Landeantriebszeit ($\tau_p$) und die Landegeschwindigkeit ($v_L$).
Am Anfang, wenn die Zeit wesentlich kleiner ist als die charakteristische Zeit, kann der Tangens durch sein Argument ersetzt werden. Dies bedeutet, dass die Geschwindigkeit haupts chlich aufgrund des Einflusses der Motoren abnimmt.
Die Gleichung f r ERROR:6110,0 f r ein Flugzeug w hrend der Landung ist gegeben mit die Landegeschwindigkeit ($v_L$), die Maximale Geschwindigkeit ($v_p$), der Start-/Landeantriebszeit ($\tau_p$) und der Startzeit ($t$) wie folgt:
Daher wird der Landezeit ($t_L$) mit dieser Gleichung berechnet, f r den Fall, dass die Geschwindigkeit zu diesem Zeitpunkt null ist. Dies ergibt sich zu:
Angesichts der Tatsache, dass die Geschwindigkeit in Bezug auf das Medium ($v$) w hrend der Landung in Abh ngigkeit von der Startzeit ($t$) mit die Landegeschwindigkeit ($v_L$), die Maximale Geschwindigkeit ($v_p$) und der Start-/Landeantriebszeit ($\tau_p$) gem der Gleichung:
variiert, k nnen wir die auf der Landebahn zur ckgelegte Strecke berechnen, indem wir diese Gleichung im Laufe der Zeit integrieren:
Die resultierende Gleichung ist eine N herung dritter Ordnung von $t/\tau_p$, was bedeutet, dass aerodynamische Hilfsmittel zur Bremsung im Vergleich zur Umkehr des Triebwerks erheblich reduziert sind.
Dar ber hinaus k nnen wir die Landezeit verwenden, um die erforderliche Landebahnl nge zu sch tzen.
Die Landung endet, wenn die Geschwindigkeit in Bezug auf das Medium ($v$) null wird, was bedeutet, dass der Zeit ($t$) gleich der Landezeit ($t_L$) ist, wodurch der Zurückgelegter Weg auf der Piste ($s$) auf der Landestrecke ($s_L$) reduziert wird. Mit die Maximale Beschleunigung ($a_p$) und die Landegeschwindigkeit ($v_L$) ergibt sich somit:
ID:(1968, 0)