Benützer:
Mechanismen
Iframe 
Die Rotation führt zu einer Änderung von die Winkelvariation ($\Delta\theta$), die mit der Endposition der Winkel ($\theta$) verbunden ist. Durch den Rotationsradius ist diese Änderung mit einem zurückgelegten Bogen von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) bis die Position ($s$) verbunden.
Mechanismen
ID:(15385, 0)
Winkel
Konzept
Um eine Drehung im dreidimensionalen Raum zu definieren, ist es zunächst erforderlich, die Achse zu spezifizieren, um die sich die Bewegung vollziehen wird. Sobald die Achse definiert ist, kann der Rotationswinkel angegeben werden, der um diese Achse auf den Körper angewendet werden soll. Es ist wichtig zu beachten, dass die Richtung der Achse durch die Gerade definiert wird, die durch sie verläuft und üblicherweise durch einen Einheitsvektor dargestellt wird. Der Rotationswinkel wird ebenfalls in Radiant gemessen und kann je nach gewünschter Rotationsrichtung positiv oder negativ sein.
ID:(4382, 0)
Beschreibung einer Rotation
Konzept
Bei der Beschreibung einer Rotationsbewegung können wir nicht in derselben Weise mit Abstand arbeiten wie bei der Beschreibung einer Translationsbewegung.
• In diesem Fall müssen wir zunächst die Position der Achse (Vektor) der Rotation bestimmen.
• Dann müssen wir den Abstand zwischen dem Objekt und der Rotationsachse bestimmen.
• Schließlich müssen wir den Rotationswinkel des Objekts um die Achse schätzen.
Bei einer Rotationsbewegung bleibt der Radius konstant. Änderungen des Radius gehören nicht zur Rotation, sondern zu einer Translation, die das Objekt radial durchführen kann.
ID:(4967, 0)
Rotationsachse
Konzept
Die einfachste Situation ist die, in der sich der Körper um seine eigene Achse dreht. In diesem Fall stimmt die Achse des Körpers mit der Drehachse überein, und der Winkel definiert die Rotation selbst:
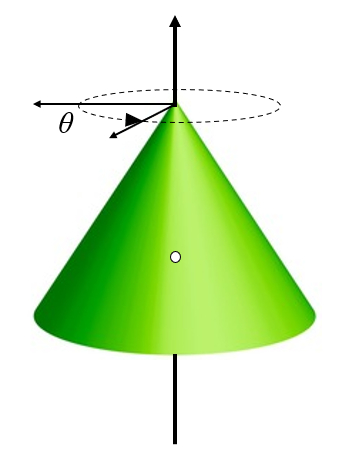
ID:(10537, 0)
Körperrotation
Konzept
Die allgemeinere Situation tritt auf, wenn die Achse des Körpers nicht mit der Rotationsachse übereinstimmt. In diesem Fall können wir uns eine vorherige Rotation des Körpers vorstellen, sodass seine Achse einen Winkel zur Rotationsachse bildet:
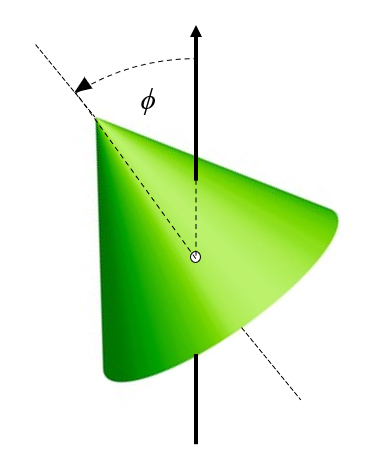
ID:(11405, 0)
Drehung eines gedrehten Körpers
Konzept
Wenn sich ein Körper dreht und seine Achse nicht mit der Rotationsachse übereinstimmt, erfährt er eine Präzession um die Rotationsachse:
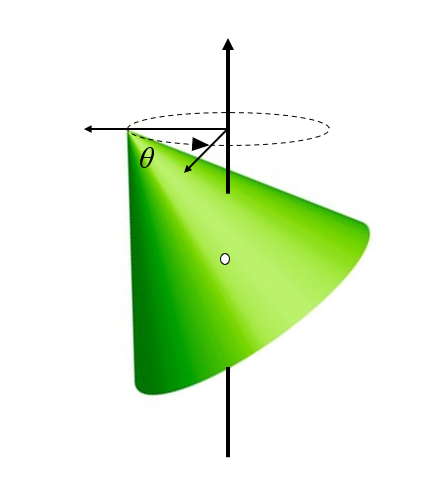
ID:(11406, 0)
Um die Körpermitte gedreht
Konzept
Abgesehen davon, ob sich die Achse des Körpers mit der Rotationsachse deckt oder nicht, gibt es auch die Situation, in der die Rotationsachse durch das geometrische Zentrum des Körpers verläuft:
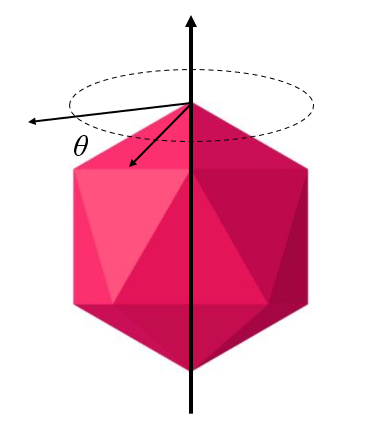
ID:(10299, 0)
Feste Achsentfernung
Konzept
Wenn die Rotationsachse nicht durch das Zentrum des Körpers verläuft, wird sich dieser nicht nur um seine eigene Achse drehen, sondern auch um die Rotationsachse herum orbitieren:
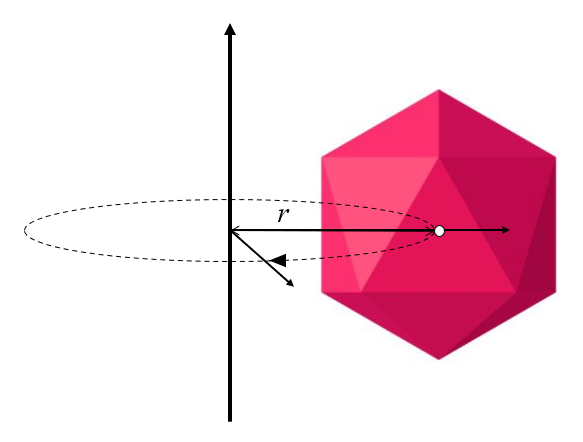
Dies ist die allgemeinste Situation, die beschrieben werden muss, wenn sich der Körper dreht.
ID:(10541, 0)
Der beim Drehen zurückgelegte Bogenmaß
Beschreibung
Wenn man einen Kreis betrachtet, wird sein Umfang $2\pi r$ sein, mit der Radius ($r$). Wenn man eine Winkelvariation ($\Delta\theta$) hat, repräsentiert es einen Bruchteil des Gesamtumfangs, gegeben durch den Ausdruck:
$\displaystyle\frac{\Delta\theta}{2\pi}$
die Zurückgelegte Strecke in einer Zeit ($\Delta s$) entspricht dem Bogen unter die Winkelvariation ($\Delta\theta$), der als dieser Bruchteil des Gesamtumfangs des Kreises berechnet werden kann:
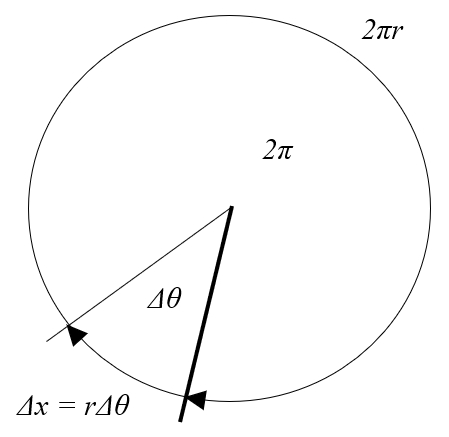
Für diese Berechnungen ist es entscheidend, dass der Winkel in Bogenmaß angegeben wird.
ID:(9879, 0)
Radians
Konzept
In der Physik ist es üblich, Bogenmaße anstelle von Grad zu verwenden, um Winkel bei Rotationen zu messen. Dies liegt daran, dass sich bei diesen Bewegungen die Objekte, die umkreisen, über Entfernungen bewegen, die Bögen eines Kreises entsprechen. Um die Geschwindigkeit des Objekts zu bestimmen, ist es notwendig, die Länge des zurückgelegten Bogens zu berechnen, was einfach ist, wenn der Radius der Umlaufbahn und der zurückgelegte Winkel in Bogenmaß bekannt sind. Aus diesem Grund werden Winkel in der Regel in Bogenmaß gemessen, um die Notwendigkeit ständiger Umrechnungen zwischen Grad und Bogenmaß bei der Durchführung von Berechnungen dieser Art zu vermeiden.
ID:(311, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta s=r \Delta\theta $
Ds = r * Dtheta
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$ \Delta\theta = \theta - \theta_0 $
Dtheta = theta - theta_0
ID:(15386, 0)
Winkel Differenz
Gleichung
Um die Rotation eines Objekts zu beschreiben, müssen wir die Winkelvariation ($\Delta\theta$) bestimmen. Dies geschieht, indem wir der Anfangswinkel ($\theta_0$) von der Winkel ($\theta$) subtrahieren, den Wert, den das Objekt während seiner Rotation erreicht:
| $ \Delta\theta = \theta - \theta_0 $ |
ID:(3680, 0)
Zurückgelegten Strecke
Gleichung
Wir können die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Bogen zurückgelegt
Gleichung
Die Position die Zurückgelegte Strecke in einer Zeit ($\Delta s$) in einer Kreisbewegung kann aus die Winkelvariation ($\Delta\theta$) und der Radius ($r$) der Umlaufbahn mithilfe der folgenden Formel berechnet werden:
| $ \Delta s=r \Delta\theta $ |
Wenn ein Objekt einen Abstand von der Radius ($r$) von einer Achse entfernt ist und eine Drehung von eine Winkelvariation ($\Delta\theta$) durchführt, was mit der Winkel ($\theta$) und der Anfangswinkel ($\theta_0$) ergibt
| $ \Delta\theta = \theta - \theta_0 $ |
wird es eine Strecke von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) zurückgelegt haben, was mit die Position ($s$) und die Ausgangsstellung ($s_0$) ergibt
| $ \Delta s \equiv s - s_0 $ |
Diese Strecke kann berechnet werden, indem man der Radius ($r$) mit dem Winkel multipliziert, also
| $ \Delta s=r \Delta\theta $ |
.
ID:(5302, 0)