Constant acceleration
Storyboard 
To reach a certain velocity, an object must first increase its velocity from rest. This process is called acceleration and is defined in terms of the change in velocity over time. Conversely, if the goal is to reduce speed or even bring the object to a stop, deceleration occurs, with the acceleration having the opposite sign to the velocity (positive velocity corresponds to negative acceleration, and vice versa), a process commonly referred to as braking.
ID:(609, 0)
Constant acceleration
Storyboard 
To reach a certain velocity, an object must first increase its velocity from rest. This process is called acceleration and is defined in terms of the change in velocity over time. Conversely, if the goal is to reduce speed or even bring the object to a stop, deceleration occurs, with the acceleration having the opposite sign to the velocity (positive velocity corresponds to negative acceleration, and vice versa), a process commonly referred to as braking.
Variables
Calculations
Calculations
Equations
In the case where the constant Acceleration ($a_0$) equals the mean Acceleration ($\bar{a}$), it will be equal to
Therefore, considering the speed Diference ($\Delta v$) as
and the time elapsed ($\Delta t$) as
the equation for the constant Acceleration ($a_0$)
can be written as
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
and by rearranging, we obtain
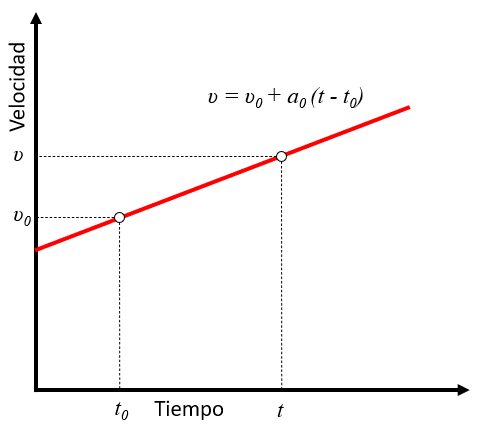
In the case of the constant Acceleration ($a_0$), the speed ($v$) as a function of the time ($t$) forms a straight line passing through the start Time ($t_0$) and the initial Speed ($v_0$), defined by the equation:
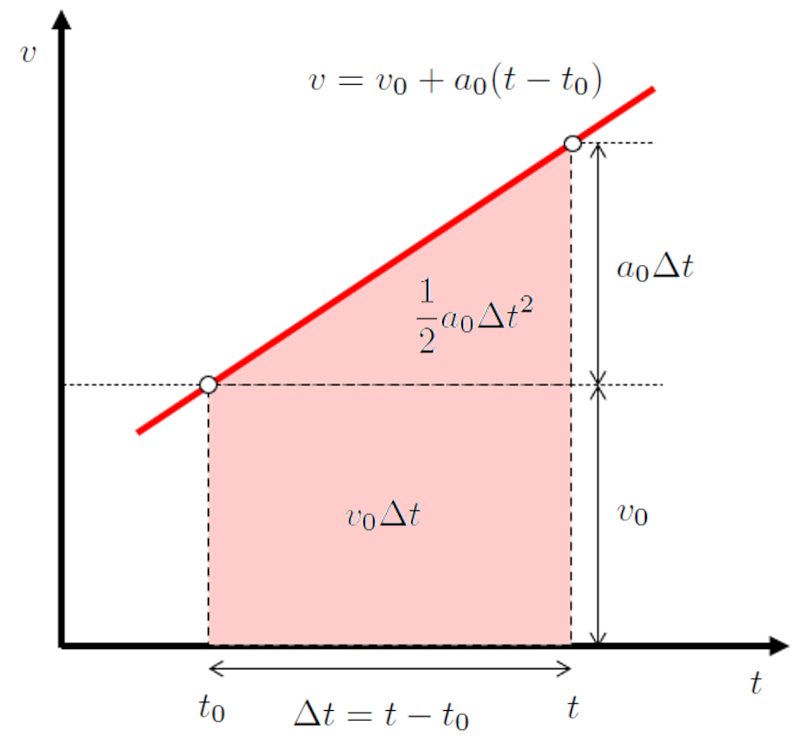
Since the distance traveled in a time ($\Delta s$) represents the area under the velocity-time curve, we can sum the contributions of the rectangle:
$v_0(t-t_0)$
and the triangle:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
To obtain the distance traveled in a time ($\Delta s$) with the position ($s$) and the starting position ($s_0$), resulting in:
Therefore:
If we solve for the time ($t$) and the start Time ($t_0$) in the equation of the speed ($v$), which depends on the initial Speed ($v_0$) and the constant Acceleration ($a_0$):
we get:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
And when we substitute this into the equation of the position ($s$) with the starting position ($s_0$):
we obtain an expression for the distance traveled as a function of velocity:
The definition of the mean Acceleration ($\bar{a}$) is considered as the relationship between the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$). That is,
and
The relationship between both is defined as the centrifuge Acceleration ($a_c$)
within this time interval.
Examples
The general structure of the model of the constant Acceleration ($a_0$) is such that on one hand it equates to the mean Acceleration ($\bar{a}$), thereby establishing the relationship between the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$).
On the other hand, there are three relationships surrounding the constant Acceleration ($a_0$) where it is associated with the speed ($v$) and the time ($t$) ($v, t$), with the position ($s$) and the time ($t$) ($s, t$), or the position ($s$) and the speed ($v$) ($s, v$):
Finally, these relationships are associated with parameters that are not shown, which are the starting position ($s_0$), the initial Speed ($v_0$), and the start Time ($t_0$), and depending on the coordinate system used, they can be defined as null. This means initiating movement at the origin ($s_0=0$), starting to measure from the origin of time ($t_0=0$), and the origin of the coordinate system being at rest relative to the observer, so there is no initial velocity ($v_0=0$).
When the velocity is not constant, it is of interest to know how it is increasing or decreasing. For this purpose, it is important to know the change in velocity per unit of time, which we call acceleration or deceleration depending on whether it is an increase or decrease.
If we travel at a speed of 100 km/hour and brake, reducing the velocity by 10 km/hour per second, we know that we will come to a stop in 10 seconds.
It is based on the measurement of the change in velocity and the change in time.
When acceleration is constant, the variation of velocity, represented by the speed ($v$), changes linearly with respect to, the time ($t$). This can be calculated using the initial Speed ($v_0$), the constant Acceleration ($a_0$), and the start Time ($t_0$), giving us the equation:
This relationship is graphically represented as a straight line, as shown below:
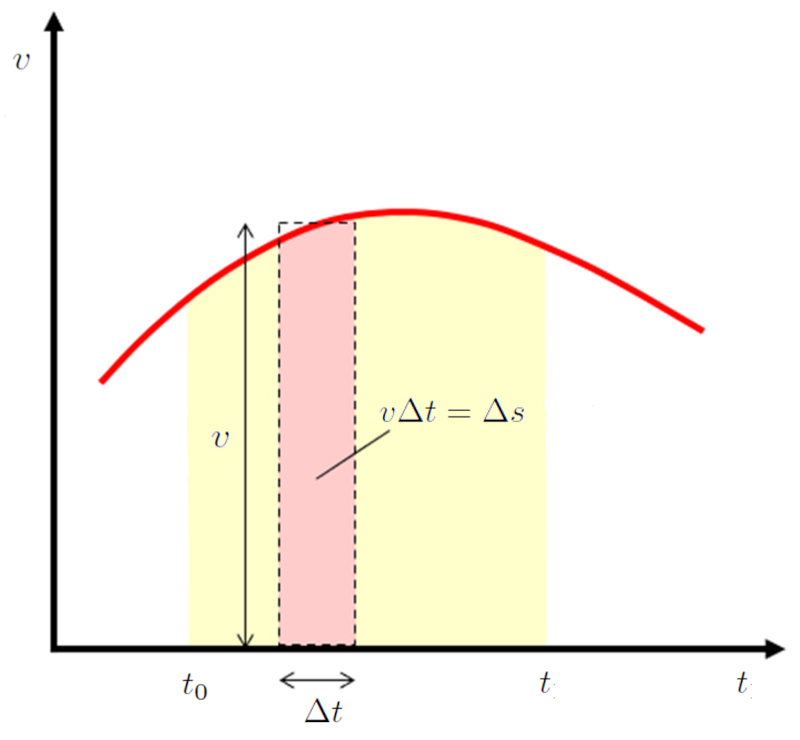
If we consider an area with width $\Delta t$ on a velocity versus time graph, it represents the displacement during that time:
In the particular case where acceleration is constant, velocity is represented on the velocity versus time graph as a straight line. This line is defined by the speed ($v$), the initial Speed ($v_0$), the constant Acceleration ($a_0$), the time ($t$), and the start Time ($t_0$), equal to:
and is graphed as follows:
Since the area under the curve can be represented as the sum of a rectangle with area
$v_0(t-t_0)$
and a triangle with area
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
We can calculate the displacement the distance traveled in a time ($\Delta s$) from the position ($s$) and the starting position ($s_0$), leading us to:
Therefore, the position ($s$) is equal to:
If we solve the equation for the speed ($v$) to find the constant Acceleration ($a_0$) with the initial Speed ($v_0$) and the start Time ($t_0$):
and substitute it into the equation for the position ($s$) with the starting position ($s_0$):
we obtain the path as a function of velocity:
From this relationship, we can see that both the acceleration path and the braking path depend on the square of the final/initial velocity. In other words, doubling the velocity requires a path four times longer.
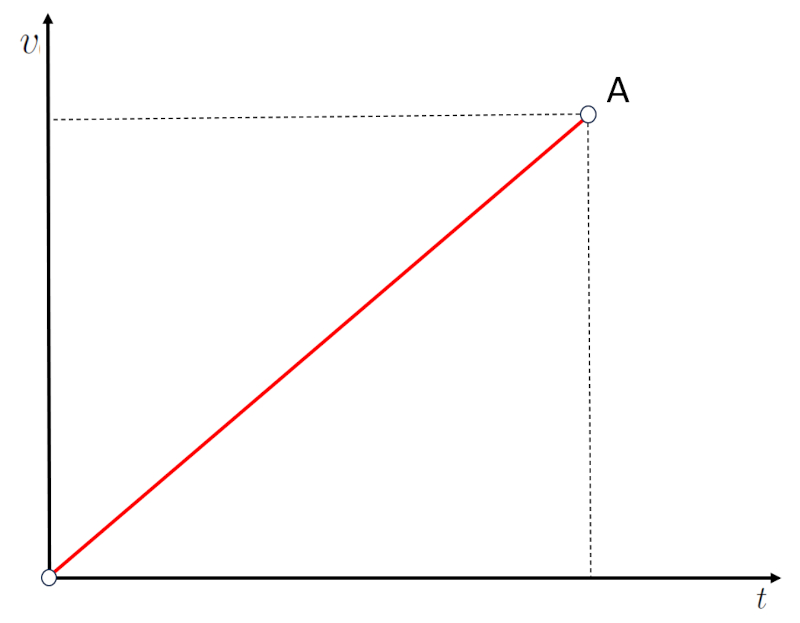
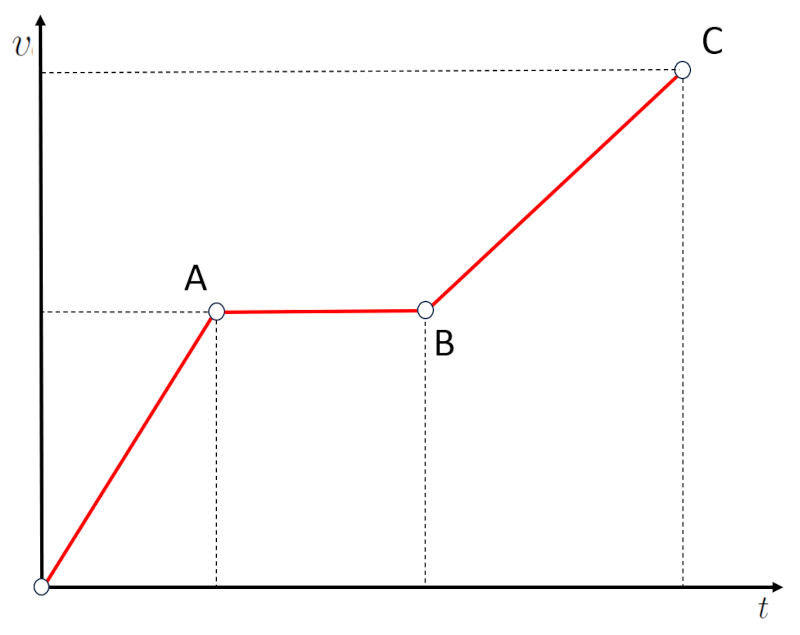
If the velocity is graphed as a line between the velocity it had at O and that at A:
it can be observed that the velocity has increased over the elapsed time. Therefore, the slope of the velocity vs elapsed time graph corresponds to the acceleration.
If the slope is steeper, it means that there is a greater increase in velocity in less time, which corresponds to a higher acceleration.
If the slope is shallower, it means that there is a smaller increase in velocity in more time, which corresponds to a lower acceleration.
One type of scenario in the velocity vs. time graph is when there are horizontal segments:
If we observe the segment AB, we can see that despite the passage of time, the velocity has not changed. This means that the object is traveling with constant velocity (careful, this does NOT mean that it has stopped). Therefore, horizontal segments, which correspond to zero slope, correspond to stages where the acceleration is zero.
In the case of the graph in which a segment has negative slope:
it represents a situation in which the velocity decreases between B and C returning to zero. In other words, negative slopes correspond in this case to a braking process.
For positive velocities, negative slopes correspond to a braking process. However, for negative velocities, a negative slope corresponds to an increase in negative velocity and thus to acceleration. In the case of negative velocities, positive acceleration corresponds to a braking process.
A braking process is one in which the acceleration has the opposite sign to that of the velocity.
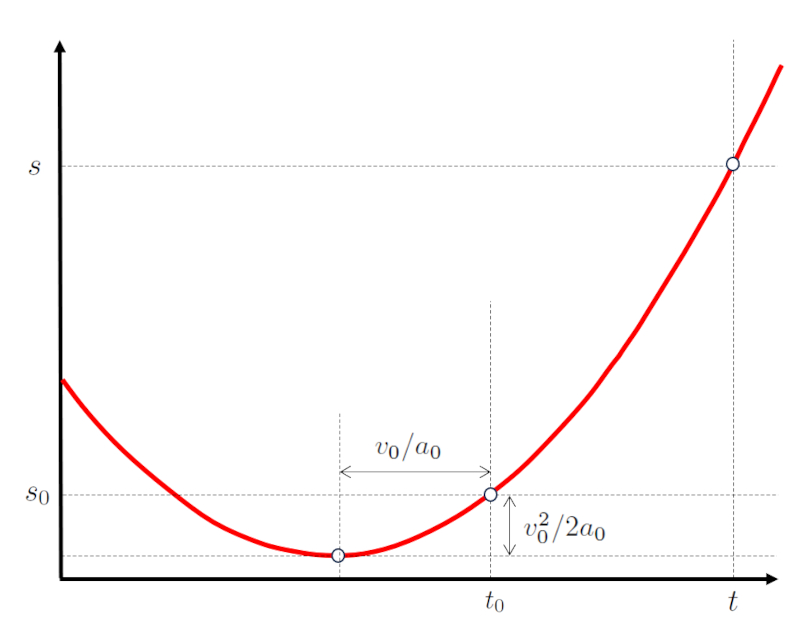
For the case of the constant Acceleration ($a_0$), the position ($s$) is a function of the time ($t$) expressed in terms of the initial Speed ($v_0$), the starting position ($s_0$), and the start Time ($t_0$):
which corresponds to a parabola:
The parabola is normal if the acceleration is positive ($a_0>0$) and inverted if it is negative ($a_0<0$).
If $v_0/a_0$ is positive, the minimum ($a_0>0$) or maximum ($a_0<0$) occurs before the initial time, so the evolution will not show a change in sign in velocity, as the slope of the curve does not change sign.
If $v_0/a_0$ is negative, the minimum ($a_0>0$) or maximum ($a_0<0$) occurs after the initial time, resulting in a reversal of movement in the future.
In the case of being a minimum ($a_0>0$), it is located at a position below the initial position by a distance of $v_0^2/2a_0$. Similarly, if it is a maximum ($a_0<0$), it will be located at a position above the initial position by a distance of $v_0^2/2a_0$.
A common situation is when acceleration is constant, meaning that velocity increases proportionally to the elapsed time.
Therefore the constant Acceleration ($a_0$),
$a_0=g$
An example of constant acceleration is the acceleration due to gravity experienced by objects falling on the surface of the planet. On the surface of the Earth, this acceleration is $9.8 m/s^2$ and is generally denoted by the letter $g$. In fact, there is a unit of measurement called $g$ that corresponds to $9.8 m/s^2$.
A body moving at a constant velocity does not experience acceleration.
Therefore, in the case where the constant Acceleration ($a_0$) is zero,
$a_0=0$
the position ($s$), with the starting position ($s_0$), the initial Speed ($v_0$), the time ($t$), and the start Time ($t_0$),
reduces to the case of constant velocity:
If the constant Acceleration ($a_0$) is equated with the mean Acceleration ($\bar{a}$), the definition of the mean Acceleration ($\bar{a}$) is associated with the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$), and on the other hand, the line that allows the calculation of the speed ($v$) in terms of the initial Speed ($v_0$), the time ($t$), and the start Time ($t_0$) is considered. Using the velocity relationship, the position ($s$) can be calculated based on the starting position ($s_0$), the initial Speed ($v_0$), the time ($t$), and the start Time ($t_0$), or based on the starting position ($s_0$), the speed ($v$), and the initial Speed ($v_0$). Both equations include the constant Acceleration ($a_0$). Finally, the distance traveled in a time ($\Delta s$), the time elapsed ($\Delta t$), and the speed Diference ($\Delta v$) are included, in which the final value is subtracted from the initial value:
Acceleration corresponds to the change in velocity per unit of time.
Therefore, it is necessary to define the speed Diference ($\Delta v$) in terms of the speed ($v$) and the initial Speed ($v_0$) as follows:
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
The proportion in which the variation of velocity over time is defined as the mean Acceleration ($\bar{a}$). To measure it, it is necessary to observe the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$).
One common method for measuring average acceleration involves using a stroboscopic lamp that illuminates the object at defined intervals. By taking a photograph, one can determine the distance traveled by the object in that time. By calculating two consecutive velocities, one can determine their variation and, with the time elapsed between the photos, the average acceleration.
The equation that describes average acceleration is as follows:
It is important to note that average acceleration is an estimation of actual acceleration.
The main problem is that if acceleration varies during the elapsed time, the value of the average acceleration may differ greatly from the mean acceleration
.
Therefore, the key is to
Determine acceleration over a sufficiently short period of time to minimize variation.
If the constant Acceleration ($a_0$), then the mean Acceleration ($\bar{a}$) is equal to the value of acceleration, that is,
In this case, the speed ($v$) as a function of the time ($t$) can be calculated by considering that it is associated with the difference between the speed ($v$) and the initial Speed ($v_0$), as well as the time ($t$) and the start Time ($t_0$).
This equation thus represents a straight line in velocity-time space.
In the case of ERROR:5297.1, the speed ($v$) varies linearly with the time ($t$), using the initial Speed ($v_0$) and the start Time ($t_0$):
Thus, the area under this line can be calculated, yielding the distance traveled in a time ($\Delta s$). Combining this with the starting position ($s_0$), we can calculate the position ($s$), resulting in:
This corresponds to the general form of a parabola.
In the case of constant acceleration, we can calculate the position ($s$) from the starting position ($s_0$), the initial Speed ($v_0$), the time ($t$), and the start Time ($t_0$) using the equation:
This allows us to determine the relationship between the distance covered during acceleration/deceleration and the change in velocity:
We can calculate the distance traveled in a time ($\Delta s$) from the starting position ($s_0$) and the position ($s$) using the following equation:
ID:(609, 0)