Porosidade geral
Storyboard 
A formulação do modelo de solo diferencia três materiais diferentes e suas proporções relativas. No entanto, ao considerar a maneira como os grãos estão dispostos, fica evidente que inevitavelmente existem espaços entre eles que precisam ser descritos. Esses espaços são cruciais, uma vez que o movimento e a difusão da água dependem deles. Portanto, é necessário primeiro introduzir o conceito de porosidade e estabelecer critérios para sua presença, além de entender como ela pode variar. Posteriormente, poderemos estudar seu efeito no comportamento do solo.
ID:(361, 0)
Porosidade de um sistema granular
Conceito 
Se você tem um material granular, sempre haverá espaço entre os grãos. Mesmo na forma mais otimizada de compactação dos grãos, sempre haverá algum espaço que não pode ser utilizado. No caso de esferas, a compactação máxima é alcançada quando três delas são agrupadas com outra colocada por cima, formando uma pirâmide com base triangular. Nesse caso, o espaço não utilizado é reduzido a apenas 25%:
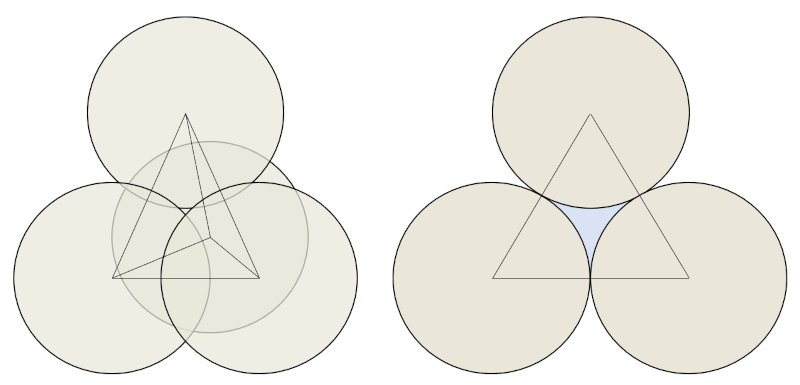
Para ilustrar melhor como esses espaços se formam, ao lado da pirâmide com base triangular, mostramos um caso bidimensional em que o espaço entre os grãos foi destacado em azul.
O que é observado aqui como espaço entre alguns grãos pode ser extrapolado para toda a amostra. Portanto, em uma amostra de areia que é vibrada até que os grãos estejam arranjados de forma otimizada, observa-se que um total de 25% do espaço permanece vago. Em um nível macroscópico, isso é conhecido como o volume de poro ($V_p$).
ID:(2072, 0)
Porosidade com grãos de diferentes tamanhos
Conceito 
Como mencionado anteriormente, se o solo fosse composto apenas por grãos de areia, teríamos uma estrutura com espaços gerados devido à incapacidade de preencher completamente esses espaços:

Estrutura base de um sistema de esferas (discos) com máxima compactação.
No entanto, os grãos de areia têm um tamanho de cerca de um milímetro, enquanto os grãos de silte têm apenas algumas dezenas de micrômetros e os de argila são ainda menores, na faixa de apenas alguns micrômetros.
Comparação entre os grãos de areia, silte e argila.
Isso significa que um grão de areia é aproximadamente 300 vezes maior que um grão de silte e aproximadamente 1000 vezes maior que um grão de argila. Portanto, se adicionarmos argila ou silte à areia, esse material pode ocupar os espaços entre os grãos de areia:

Espaços entre os grãos de areia preenchidos com silte e argila, ou silte preenchido com argila.
ID:(2079, 0)
Porosidade mínima da areia
Variable 
No caso das esferas, é alcançada uma disposição ótima em que o espaço vazio em relação ao volume total, correspondente à porosidade ideal do modelo que chamaremos de la própria porosidade da areia ($q_a$), é da ordem de:
$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$
Esse valor foi inicialmente proposto no século XVII por Johannes Kepler e era conhecido como 'conjectura de Kepler'. No entanto, só foi comprovado em 1998 por Thomas C. Hales.
ID:(3172, 0)
Porosidade mínima do lodo
Variable 
No caso do limo, que é modelado como pequenos cubos, surgem forças entre os grãos nessa escala que distorcem a maneira como eles se organizam. Por essa razão, não existem empilhamentos ótimos de cubos uns sobre os outros, mas sim uma estrutura em que la própria porosidade do lodo ($q_i$) tem uma ordem de magnitude aproximada de:
$q_i \sim \displaystyle\frac{1}{3}$
.
ID:(15079, 0)
Porosidade mínima da argila
Variable 
No caso da argila, que é modelada como pequenas lâminas, surgem forças entre os grãos nessa escala que alteram a forma como eles se organizam. Por essa razão, não existem empilhamentos ótimos de lâminas umas sobre as outras, mas sim uma estrutura em que la própria porosidade do lodo ($q_i$) tem uma ordem de magnitude aproximada de:
$q_c\sim \displaystyle\frac{2}{5}$
ID:(15080, 0)
Distribuição de grãos no solo
Conceito 
Os grãos de sedimento no solo podem estar distribuídos de forma aleatória, o que significa que eles não formam concentrações de um tipo particular de grão. Isso resultaria em grãos de areia e silte, devido ao seu tamanho e quantidade, estarem dispersos dentro de uma matriz de argila:

Distribuição homogênea de grãos.
No entanto, também existe a possibilidade de que eles possam estar agrupados por tipo, com uma penetração limitada. Em outras palavras, os grãos de argila poderiam ocupar pelo menos parte dos espaços dentro de uma estrutura separada de grãos de areia e silte:

Distribuição de grãos com conglomerados específicos por tipo.
A forma como o solo se sedimenta pode resultar em camadas separadas de areia, silte e argila. Por outro lado, o movimento do solo pode desencadear processos de mistura.
ID:(925, 0)
Cálculo de volume por componente
Conceito 
Se considerarmos um único grão, podemos distinguir seu volume individual, representado como $V_q$, e a fração dentro do volume total $V$ que corresponde ao espaço vazio (porosidade):
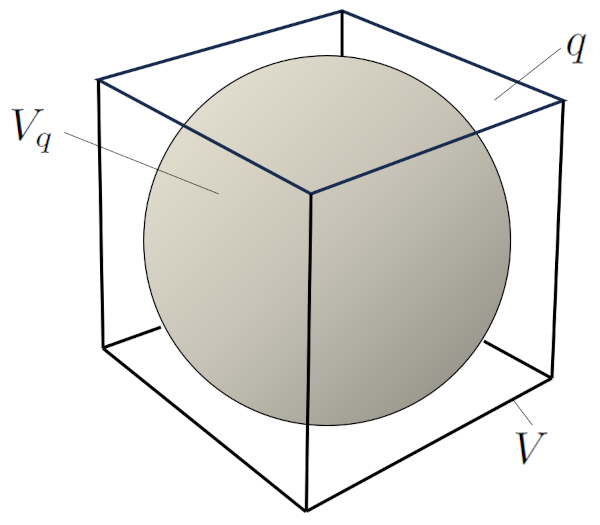
Isso implica que $1-q$ representa a fração do volume $V$ ocupada pelo volume sólido $V_q$. Portanto,
$V_q = (1-q)V$
Portanto, o volume associado a um grão (volume sólido e porosidade associada ao grão) é
$V=\displaystyle\frac{1}{1-q}V_q$
O que é expresso aqui em relação a um único grão também é válido para todos os grãos dentro de um componente. Em outras palavras, podemos considerar $V_q$ como o volume sólido de todo o componente $q$.
ID:(2075, 0)
Volume de macroporos
Conceito 
A porosidade inerente à estrutura dos grãos refere-se a um tipo de porosidade que é microscópica e é conhecida como porosidade primária. No entanto, o solo também pode conter espaços que podem fechar devido a deformações, seja de forma natural ou como resultado de intervenções externas.
Deformações naturais podem estar relacionadas a processos de secagem que resultam em uma redução de volume e na formação de fissuras. Outro mecanismo envolve forças geológicas, como terremotos ou movimentos induzidos pela gravidade. Por outro lado, intervenções humanas incluem atividades agrícolas comuns, como arar e outros processos de movimentação de terra.
Vamos nos referir a esses espaços resultantes de deformações como o volume de macroporos ($V_m$).
Esse tipo de porosidade pode ser observado diretamente em uma amostra de solo. No exemplo a seguir, há três amostras: uma com um alto conteúdo de macroporos, outra com alguns macroporos e a última praticamente sem presença deles:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004
ID:(2071, 0)
Modelos de volume e porosidade
Conceito 
A porosidade refere-se ao espaço vazio dentro da estrutura do solo. No entanto, existem dois tipos de porosidade: micro e macro porosidade. A diferença está no fato de que a micro porosidade é inerente à estrutura dos grãos do solo e não pode ser modificada sem afetar a forma como os grãos se empilham em um nível microscópico. O segundo tipo de porosidade é gerado por processos internos ou pela forma como o solo é manipulado.
Consequentemente, existem duas maneiras de decompor o volume total do solo:
Com base na macroporosidade:
• o volume de macroporos ($V_m$): Macroporosidade que não depende da estrutura microscópica do solo.
• o volume próprio ($V_z$): O volume ocupado pelos grãos, incluindo os microporos gerados ao empilhá-los.
Com base na porosidade independente de sua origem:
• o volume de poro ($V_p$): Porosidade geralmente independente de sua origem.
• o volume sólido ($V_s$): O volume ocupado pelos grãos, excluindo a microporosidade gerada ao empilhá-los.
Essa estrutura pode ser representada da seguinte forma:
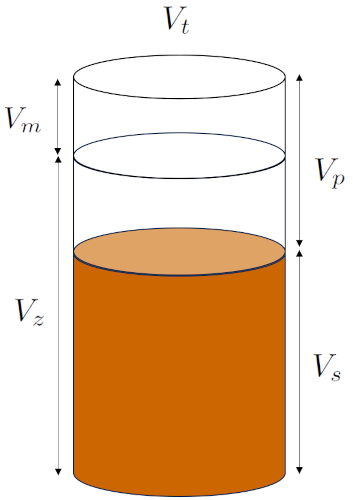
ID:(15090, 0)
Porosidade geral
Modelo 
A formulação do modelo de solo diferencia três materiais diferentes e suas proporções relativas. No entanto, ao considerar a maneira como os grãos estão dispostos, fica evidente que inevitavelmente existem espaços entre eles que precisam ser descritos. Esses espaços são cruciais, uma vez que o movimento e a difusão da água dependem deles. Portanto, é necessário primeiro introduzir o conceito de porosidade e estabelecer critérios para sua presença, além de entender como ela pode variar. Posteriormente, poderemos estudar seu efeito no comportamento do solo.
Variáveis
Cálculos
Cálculos
Equações
La própria porosidade da areia ($q_a$) representa a fra o do volume $V$ que corresponde aos espa os vazios entre os gr os de areia. Portanto, $1-q_a$ a fra o de o volume sólido de areia ($V_a$) em rela o a $V$:
$1 - q_a = \displaystyle\frac{V_a}{V}$
Consequentemente, o volume ocupado pelos gr os de areia :
$\displaystyle\frac{V_a}{1 - q_a}$
Da mesma forma, para o silte, usamos la própria porosidade do lodo ($q_i$) e o volume sólido de lodo ($V_i$), ent o o volume ocupado pelos gr os de sil
te :
$\displaystyle\frac{V_i}{1 - q_i}$
E para a argila, usamos la própria porosidade da argila ($q_c$) e o volume sólido de argila ($V_c$). Portanto, o volume ocupado pelos gr os de argila :
$\displaystyle\frac{V_c}{1 - q_c}$
Em resumo, o volume total a soma desses volumes, ou seja,
| $ V_z = \displaystyle\frac{1}{1- q_a } V_a + \displaystyle\frac{1}{1- q_i } V_i + \displaystyle\frac{1}{1- q_c } V_c $ |
(ID 2077)
(ID 4726)
Com o volume total ($V_t$) expresso em termos de o volume de macroporos ($V_m$) e o volume próprio ($V_z$) como
| $ V_t = V_m + V_z $ |
e considerando o volume sólido ($V_s$) e o volume de poro ($V_p$), chegamos a
| $ V_t = V_s + V_p $ |
o que nos leva equa o
$V_m + V_z = V_s + V_p$
e, portanto,
| $ V_p = V_m + V_z - V_s $ |
(ID 10556)
Se voc tiver la porosidade ($f$) conforme fornecido pela equa o:
| $ f =\displaystyle\frac{ V_p }{ V_t }$ |
e o volume sólido ($V_s$) obtido por meio da seguinte equa o:
| $ V_t = V_s + V_p $ |
voc pode eliminar o volume total ($V_t$) e obter o volume de poro ($V_p$) da seguinte forma:
| $ V_p =\displaystyle\frac{ f }{1- f } V_s $ |
(ID 10590)
O volume de poro ($V_p$) pode ser calculado usando o volume de macroporos ($V_m$), o volume próprio ($V_z$), e o volume sólido ($V_s$) atrav s da equa o
| $ V_p = V_m + V_z - V_s $ |
onde o volume sólido ($V_s$) calculado usando o volume sólido de areia ($V_a$), o volume sólido de lodo ($V_i$) e o volume sólido de argila ($V_c$) conforme
| $ V_s = V_a + V_l + V_c $ |
e a rela o
| $ V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$ |
usada para obter
| $ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $ |
(ID 15081)
(ID 15085)
Exemplos
(ID 15198)
Se voc tem um material granular, sempre haver espa o entre os gr os. Mesmo na forma mais otimizada de compacta o dos gr os, sempre haver algum espa o que n o pode ser utilizado. No caso de esferas, a compacta o m xima alcan ada quando tr s delas s o agrupadas com outra colocada por cima, formando uma pir mide com base triangular. Nesse caso, o espa o n o utilizado reduzido a apenas 25%:

Para ilustrar melhor como esses espa os se formam, ao lado da pir mide com base triangular, mostramos um caso bidimensional em que o espa o entre os gr os foi destacado em azul.
O que observado aqui como espa o entre alguns gr os pode ser extrapolado para toda a amostra. Portanto, em uma amostra de areia que vibrada at que os gr os estejam arranjados de forma otimizada, observa-se que um total de 25% do espa o permanece vago. Em um n vel macrosc pico, isso conhecido como o volume de poro ($V_p$).
(ID 2072)
Como mencionado anteriormente, se o solo fosse composto apenas por gr os de areia, ter amos uma estrutura com espa os gerados devido incapacidade de preencher completamente esses espa os:

Estrutura base de um sistema de esferas (discos) com m xima compacta o.
No entanto, os gr os de areia t m um tamanho de cerca de um mil metro, enquanto os gr os de silte t m apenas algumas dezenas de micr metros e os de argila s o ainda menores, na faixa de apenas alguns micr metros.

Compara o entre os gr os de areia, silte e argila.
Isso significa que um gr o de areia aproximadamente 300 vezes maior que um gr o de silte e aproximadamente 1000 vezes maior que um gr o de argila. Portanto, se adicionarmos argila ou silte areia, esse material pode ocupar os espa os entre os gr os de areia:

Espa os entre os gr os de areia preenchidos com silte e argila, ou silte preenchido com argila.
(ID 2079)
No caso das esferas, alcan ada uma disposi o tima em que o espa o vazio em rela o ao volume total, correspondente porosidade ideal do modelo que chamaremos de la própria porosidade da areia ($q_a$), da ordem de:
$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$
Esse valor foi inicialmente proposto no s culo XVII por Johannes Kepler e era conhecido como 'conjectura de Kepler'. No entanto, s foi comprovado em 1998 por Thomas C. Hales.
(ID 3172)
No caso do limo, que modelado como pequenos cubos, surgem for as entre os gr os nessa escala que distorcem a maneira como eles se organizam. Por essa raz o, n o existem empilhamentos timos de cubos uns sobre os outros, mas sim uma estrutura em que la própria porosidade do lodo ($q_i$) tem uma ordem de magnitude aproximada de:
$q_i \sim \displaystyle\frac{1}{3}$
.
(ID 15079)
No caso da argila, que modelada como pequenas l minas, surgem for as entre os gr os nessa escala que alteram a forma como eles se organizam. Por essa raz o, n o existem empilhamentos timos de l minas umas sobre as outras, mas sim uma estrutura em que la própria porosidade do lodo ($q_i$) tem uma ordem de magnitude aproximada de:
$q_c\sim \displaystyle\frac{2}{5}$
(ID 15080)
Os gr os de sedimento no solo podem estar distribu dos de forma aleat ria, o que significa que eles n o formam concentra es de um tipo particular de gr o. Isso resultaria em gr os de areia e silte, devido ao seu tamanho e quantidade, estarem dispersos dentro de uma matriz de argila:

Distribui o homog nea de gr os.
No entanto, tamb m existe a possibilidade de que eles possam estar agrupados por tipo, com uma penetra o limitada. Em outras palavras, os gr os de argila poderiam ocupar pelo menos parte dos espa os dentro de uma estrutura separada de gr os de areia e silte:

Distribui o de gr os com conglomerados espec ficos por tipo.
A forma como o solo se sedimenta pode resultar em camadas separadas de areia, silte e argila. Por outro lado, o movimento do solo pode desencadear processos de mistura.
(ID 925)
Se considerarmos um nico gr o, podemos distinguir seu volume individual, representado como $V_q$, e a fra o dentro do volume total $V$ que corresponde ao espa o vazio (porosidade):

Isso implica que $1-q$ representa a fra o do volume $V$ ocupada pelo volume s lido $V_q$. Portanto,
$V_q = (1-q)V$
Portanto, o volume associado a um gr o (volume s lido e porosidade associada ao gr o)
$V=\displaystyle\frac{1}{1-q}V_q$
O que expresso aqui em rela o a um nico gr o tamb m v lido para todos os gr os dentro de um componente. Em outras palavras, podemos considerar $V_q$ como o volume s lido de todo o componente $q$.
(ID 2075)
A porosidade inerente estrutura dos gr os refere-se a um tipo de porosidade que microsc pica e conhecida como porosidade prim ria. No entanto, o solo tamb m pode conter espa os que podem fechar devido a deforma es, seja de forma natural ou como resultado de interven es externas.
Deforma es naturais podem estar relacionadas a processos de secagem que resultam em uma redu o de volume e na forma o de fissuras. Outro mecanismo envolve for as geol gicas, como terremotos ou movimentos induzidos pela gravidade. Por outro lado, interven es humanas incluem atividades agr colas comuns, como arar e outros processos de movimenta o de terra.
Vamos nos referir a esses espa os resultantes de deforma es como o volume de macroporos ($V_m$).
Esse tipo de porosidade pode ser observado diretamente em uma amostra de solo. No exemplo a seguir, h tr s amostras: uma com um alto conte do de macroporos, outra com alguns macroporos e a ltima praticamente sem presen a deles:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004
(ID 2071)
A porosidade refere-se ao espa o vazio dentro da estrutura do solo. No entanto, existem dois tipos de porosidade: micro e macro porosidade. A diferen a est no fato de que a micro porosidade inerente estrutura dos gr os do solo e n o pode ser modificada sem afetar a forma como os gr os se empilham em um n vel microsc pico. O segundo tipo de porosidade gerado por processos internos ou pela forma como o solo manipulado.
Consequentemente, existem duas maneiras de decompor o volume total do solo:
Com base na macroporosidade:
• o volume de macroporos ($V_m$): Macroporosidade que n o depende da estrutura microsc pica do solo.
• o volume próprio ($V_z$): O volume ocupado pelos gr os, incluindo os microporos gerados ao empilh -los.
Com base na porosidade independente de sua origem:
• o volume de poro ($V_p$): Porosidade geralmente independente de sua origem.
• o volume sólido ($V_s$): O volume ocupado pelos gr os, excluindo a microporosidade gerada ao empilh -los.
Essa estrutura pode ser representada da seguinte forma:

(ID 15090)
(ID 15217)
ID:(361, 0)
