Allgemeine Porosität
Storyboard 
Die Formulierung des Bodenmodells unterscheidet drei verschiedene Materialien und ihre relativen Anteile. Bei genauer Betrachtung der Anordnung der Körner wird jedoch deutlich, dass zwangsläufig Zwischenräume zwischen ihnen vorhanden sind, die beschrieben werden müssen. Diese Zwischenräume sind entscheidend, da die Bewegung und Diffusion von Wasser von ihnen abhängen. Daher ist es zunächst notwendig, das Konzept der Porosität einzuführen und Kriterien für ihr Vorhandensein festzulegen sowie zu verstehen, wie sie variieren kann. Anschließend können wir ihre Auswirkungen auf das Verhalten des Bodens untersuchen.
ID:(361, 0)
Porosität eines körnigen Systems
Konzept 
Wenn du ein granulares Material hast, wird es immer Platz zwischen den Körnern geben. Selbst in der optimalsten Weise, die Körner zu packen, wird immer etwas Platz bleiben, der nicht genutzt werden kann. Im Fall von Kugeln wird die maximale Verdichtung erreicht, wenn drei von ihnen zusammengefügt werden und eine weitere oben platziert wird, um eine Pyramide mit einer dreieckigen Basis zu bilden. In diesem Fall wird der ungenutzte Raum auf nur 25% reduziert:
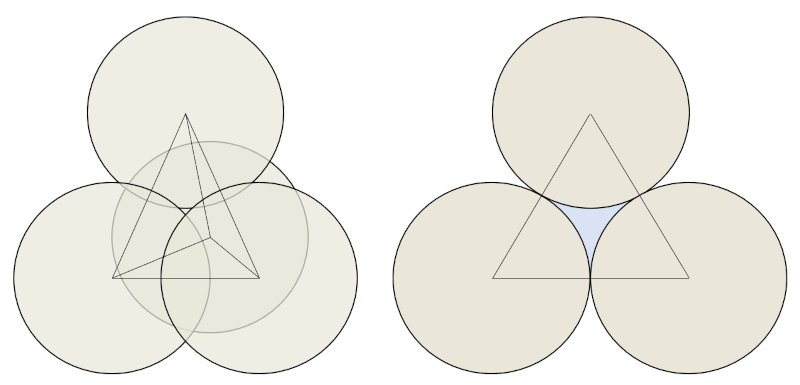
Um besser zu veranschaulichen, wie sich diese Zwischenräume bilden, zeigen wir neben der Pyramide mit der dreieckigen Basis einen zweidimensionalen Fall, in dem der Raum zwischen den Körnern blau hervorgehoben wurde.
Was hier als Raum zwischen einigen Körnern zu sehen ist, kann auf die gesamte Probe extrapoliert werden. Daher wird in einer Probe aus Sand, die so lange vibriert wird, bis die Körner optimal angeordnet sind, beobachtet, dass insgesamt 25% des Raums ungenutzt bleibt. Auf makroskopischer Ebene ist dies als der Porenvolumen ($V_p$) bekannt.
ID:(2072, 0)
Porosität mit Körnern unterschiedlicher Größe
Konzept 
Wie zuvor erwähnt, wenn der Boden nur aus Sandkörnern bestehen würde, hätten wir eine Struktur mit Zwischenräumen, die aufgrund der Unfähigkeit, diese Zwischenräume vollständig zu füllen, entstehen:

Grundstruktur eines Systems von Kugeln (Scheiben) mit maximaler Verdichtung.
Allerdings haben Sandkörner eine Größe von etwa einem Millimeter, während Schlickkörner nur einige Zehntel Mikrometer groß sind und Tonkörner noch kleiner sind, im Bereich von nur wenigen Mikrometern.
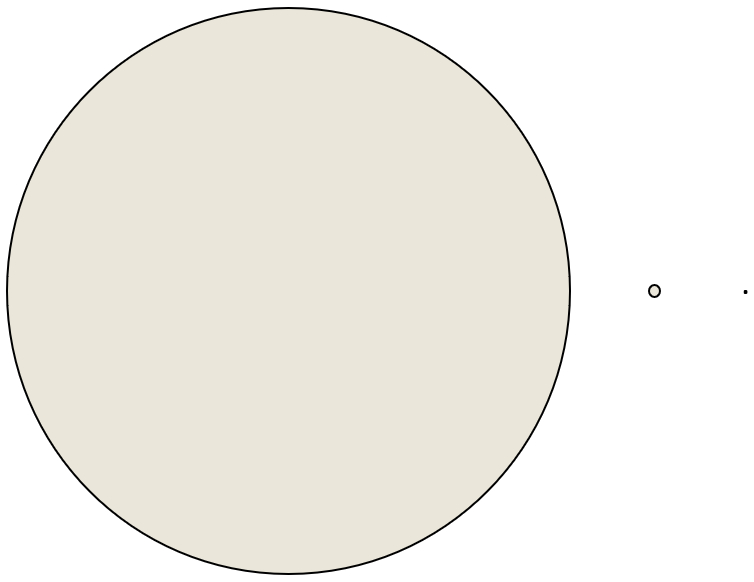
Vergleich zwischen Sand-, Schluff- und Tonkörnern.
Dies bedeutet, dass ein Sandkorn etwa 300 Mal größer ist als ein Schlickkorn und ungefähr 1000 Mal größer als ein Tonkorn. Daher kann, wenn wir Ton oder Schlick zum Sand hinzufügen, dieses Material die Zwischenräume zwischen den Sandkörnern ausfüllen:

Zwischenräume zwischen den Sandkörnern, die mit Schluff- und Tonkörnern gefüllt sind, oder Schluff, der mit Ton gefüllt ist.
ID:(2079, 0)
Minimale Sandporosität
Variable 
Im Fall von Kugeln wird eine optimale Anordnung erreicht, bei der der leere Raum im Verhältnis zum Gesamtvolumen, was der optimalen Porosität des Modells entspricht und die wir als die Eigene Porosität des Sandes ($q_a$) bezeichnen, in der Größenordnung liegt:
$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$
Dieser Wert wurde im 17. Jahrhundert erstmals von Johannes Kepler vorgeschlagen und war als 'Keplers Vermutung' bekannt. Allerdings wurde er erst im Jahr 1998 von Thomas C. Hales bewiesen.
ID:(3172, 0)
Minimale Schlammporosität
Variable 
Im Fall von Schluff, der als kleine Würfel modelliert wird, entstehen auf dieser Ebene Kräfte zwischen den Körnern, die die Art und Weise, wie sie sich anordnen, verzerren. Aus diesem Grund gibt es keine optimalen Stapelungen von Würfeln übereinander, sondern eine Struktur, in die Eigene Porosität des Schlicks ($q_i$) eine ungefähre Größenordnung von:
$q_i \sim \displaystyle\frac{1}{3}$
hat.
ID:(15079, 0)
Minimale Tonporosität
Variable 
Im Fall von Ton, der als kleine Schichten modelliert wird, entstehen auf dieser Ebene Kräfte zwischen den Körnern, die die Art und Weise, wie sie sich anordnen, verändern. Aus diesem Grund gibt es keine optimalen Stapelungen von Schichten übereinander, sondern eher eine Struktur, in die Eigene Porosität des Schlicks ($q_i$) eine ungefähre Größenordnung von:
$q_c\sim \displaystyle\frac{2}{5}$
hat.
ID:(15080, 0)
Kornverteilung im Boden
Konzept 
Die Sedimentkörner im Boden können zufällig verteilt sein, was bedeutet, dass sie keine Konzentrationen eines bestimmten Körnertyps bilden. Dies würde dazu führen, dass Sand- und Schluffkörner aufgrund ihrer Größe und Menge in einer Tonmatrix verteilt sind:

Homogene Verteilung der Körner.
Es besteht jedoch auch die Möglichkeit, dass sie nach Typ gruppiert sind und es nur eine begrenzte Durchdringung gibt. Mit anderen Worten könnten Tonkörner zumindest teilweise die Räume innerhalb einer getrennten Struktur aus Sand- und Schluffkörnern einnehmen:

Verteilung der Körner mit typspezifischen Konglomeraten.
Die Art und Weise, wie sich Boden absetzt, kann zu getrennten Schichten aus Sand, Schluff und Ton führen. Auf der anderen Seite kann die Bewegung des Bodens zu Mischprozessen führen.
ID:(925, 0)
Volumenberechnung pro Komponente
Konzept 
Wenn wir ein einzelnes Korn betrachten, können wir sein individuelles Volumen, bezeichnet als $V_q$, und den Anteil im Gesamtvolumen $V$ unterscheiden, der dem Hohlraum (Porosität) entspricht:
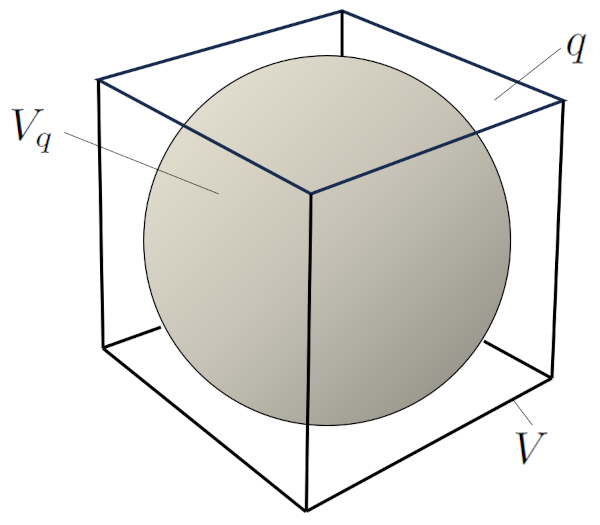
Dies impliziert, dass $1-q$ den Anteil des Volumens $V$ darstellt, der vom festen Volumen $V_q$ eingenommen wird. Daher gilt:
$V_q = (1-q)V$
Daher ist das Volumen, das mit einem Korn verbunden ist (festes Volumen und mit dem Korn verbundene Porosität):
$V=\displaystyle\frac{1}{1-q}V_q$
Was hier in Bezug auf ein einzelnes Korn ausgedrückt wird, gilt auch für alle Körner innerhalb einer Komponente. Mit anderen Worten, wir können $V_q$ als das feste Volumen der gesamten Komponente $q$ betrachten.
ID:(2075, 0)
Makroporenvolumen
Konzept 
Die in der Kornstruktur vorhandene Porosität bezieht sich auf eine Art von Porosität, die mikroskopisch ist und als Primärporosität bekannt ist. Jedoch kann der Boden auch Räume enthalten, die sich aufgrund von Verformungen schließen können, sei es auf natürliche Weise oder als Ergebnis externer Eingriffe.
Natürliche Verformungen können mit Trocknungsprozessen zusammenhängen, die zu einer Volumenreduzierung und zur Bildung von Rissen führen. Ein weiterer Mechanismus beinhaltet geologische Kräfte wie Erdbeben oder gravitationsbedingte Bewegungen. Auf der anderen Seite umfassen menschliche Eingriffe häufige landwirtschaftliche Aktivitäten wie das Pflügen und andere Erdbewegungsprozesse.
Wir werden diese durch Verformungen entstehenden Räume als der Makroporenvolumen ($V_m$) bezeichnen.
Diese Art von Porosität kann direkt in einer Bodenprobe beobachtet werden. Im folgenden Beispiel gibt es drei Proben: eine mit einem hohen Anteil an Makroporen, eine weitere mit einigen Makroporen und die letzte praktisch ohne deren Vorhandensein:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004
ID:(2071, 0)
Volumen- und Porositätsmodelle
Konzept 
Porosität bezieht sich auf den leeren Raum innerhalb der Bodenstruktur. Es gibt jedoch zwei Arten von Porosität: Mikro- und Makroporosität. Der Unterschied besteht darin, dass die Mikroporosität der Struktur der Bodenkörner inhärent ist und nicht verändert werden kann, ohne die Art und Weise zu beeinflussen, wie die Körner auf mikroskopischer Ebene gestapelt sind. Die zweite Art der Porosität entsteht durch interne Prozesse oder die Art und Weise, wie der Boden manipuliert wird.
Daher gibt es zwei Möglichkeiten, das Gesamtvolumen des Bodens aufzuschlüsseln:
In Bezug auf die Makroporosität:
der Makroporenvolumen ($V_m$): Makroporosität, die unabhängig von der mikroskopischen Bodenstruktur ist.
das Eigenvolumen ($V_z$): Das Volumen, das von den Körnern eingenommen wird, einschließlich der Mikroporen, die beim Stapeln entstehen.
Basierend auf der Porosität, unabhängig von ihrer Herkunft:
der Porenvolumen ($V_p$): Porosität, die im Allgemeinen unabhängig von ihrer Herkunft ist.
das Solides Volumen ($V_s$): Das Volumen, das von den Körnern eingenommen wird, ohne die Mikroporosität einzubeziehen, die beim Stapeln entsteht.
Diese Struktur kann wie folgt dargestellt werden:
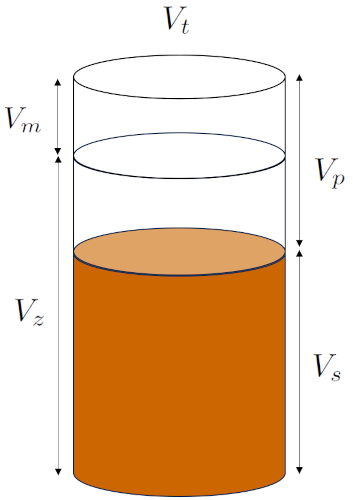
ID:(15090, 0)
Allgemeine Porosität
Modell 
Die Formulierung des Bodenmodells unterscheidet drei verschiedene Materialien und ihre relativen Anteile. Bei genauer Betrachtung der Anordnung der Körner wird jedoch deutlich, dass zwangsläufig Zwischenräume zwischen ihnen vorhanden sind, die beschrieben werden müssen. Diese Zwischenräume sind entscheidend, da die Bewegung und Diffusion von Wasser von ihnen abhängen. Daher ist es zunächst notwendig, das Konzept der Porosität einzuführen und Kriterien für ihr Vorhandensein festzulegen sowie zu verstehen, wie sie variieren kann. Anschließend können wir ihre Auswirkungen auf das Verhalten des Bodens untersuchen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Eigene Porosität des Sandes ($q_a$) repr sentiert den Anteil des Volumens $V$, der den leeren Raum zwischen den Sandk rnern darstellt. Daher ist $1-q_a$ der Anteil von das Festes Sandvolumen ($V_a$) bezogen auf $V$:
$1 - q_a = \displaystyle\frac{V_a}{V}$
Folglich ist das Volumen, das von den Sandk rnern eingenommen wird:
$\displaystyle\frac{V_a}{1 - q_a}$
hnlich verh lt es sich f r Schluff, hier verwenden wir die Eigene Porosität des Schlicks ($q_i$) und das Festes Schlammvolumen ($V_i$), daher ist das Volumen, das von den Schluffk rnern eingenommen wird:
$\displaystyle\frac{V_i}{1 - q_i}$
Und f r Ton verwenden wir die Eigene Porosität des Ton ($q_c$) und das Festes Tonvolumen ($V_c$). Das bedeutet, das Volumen, das von den Tonk rnern eingenommen wird, ist:
$\displaystyle\frac{V_c}{1 - q_c}$
Zusammengefasst ergibt sich das Gesamtvolumen als Summe dieser Volumina, das hei t:
| $ V_z = \displaystyle\frac{1}{1- q_a } V_a + \displaystyle\frac{1}{1- q_i } V_i + \displaystyle\frac{1}{1- q_c } V_c $ |
(ID 2077)
(ID 4726)
Mit das Gesamtvolumen ($V_t$) ausgedr ckt in Bezug auf der Makroporenvolumen ($V_m$) und das Eigenvolumen ($V_z$) als
| $ V_t = V_m + V_z $ |
und unter Ber cksichtigung von das Solides Volumen ($V_s$) und der Porenvolumen ($V_p$) erhalten wir
| $ V_t = V_s + V_p $ |
was uns zur Gleichung f hrt
$V_m + V_z = V_s + V_p$
und somit zu
| $ V_p = V_m + V_z - V_s $ |
(ID 10556)
Wenn Sie die Porosität ($f$) gem der folgenden Gleichung haben:
| $ f =\displaystyle\frac{ V_p }{ V_t }$ |
und das Solides Volumen ($V_s$) durch folgende Gleichung erhalten:
| $ V_t = V_s + V_p $ |
k nnen Sie das Gesamtvolumen ($V_t$) eliminieren und der Porenvolumen ($V_p$) wie folgt erhalten:
| $ V_p =\displaystyle\frac{ f }{1- f } V_s $ |
(ID 10590)
Der Porenvolumen ($V_p$) kann mithilfe von der Makroporenvolumen ($V_m$), das Eigenvolumen ($V_z$) und das Solides Volumen ($V_s$) durch die Gleichung
| $ V_p = V_m + V_z - V_s $ |
berechnet werden, wobei das Solides Volumen ($V_s$) gem
| $ V_s = V_a + V_l + V_c $ |
unter Verwendung von das Festes Sandvolumen ($V_a$), das Festes Schlammvolumen ($V_i$) und das Festes Tonvolumen ($V_c$) berechnet wird, und die Beziehung
| $ V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$ |
verwendet wird, um
| $ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $ |
(ID 15081)
(ID 15085)
Beispiele
(ID 15198)
Wenn du ein granulares Material hast, wird es immer Platz zwischen den K rnern geben. Selbst in der optimalsten Weise, die K rner zu packen, wird immer etwas Platz bleiben, der nicht genutzt werden kann. Im Fall von Kugeln wird die maximale Verdichtung erreicht, wenn drei von ihnen zusammengef gt werden und eine weitere oben platziert wird, um eine Pyramide mit einer dreieckigen Basis zu bilden. In diesem Fall wird der ungenutzte Raum auf nur 25% reduziert:

Um besser zu veranschaulichen, wie sich diese Zwischenr ume bilden, zeigen wir neben der Pyramide mit der dreieckigen Basis einen zweidimensionalen Fall, in dem der Raum zwischen den K rnern blau hervorgehoben wurde.
Was hier als Raum zwischen einigen K rnern zu sehen ist, kann auf die gesamte Probe extrapoliert werden. Daher wird in einer Probe aus Sand, die so lange vibriert wird, bis die K rner optimal angeordnet sind, beobachtet, dass insgesamt 25% des Raums ungenutzt bleibt. Auf makroskopischer Ebene ist dies als der Porenvolumen ($V_p$) bekannt.
(ID 2072)
Wie zuvor erw hnt, wenn der Boden nur aus Sandk rnern bestehen w rde, h tten wir eine Struktur mit Zwischenr umen, die aufgrund der Unf higkeit, diese Zwischenr ume vollst ndig zu f llen, entstehen:

Grundstruktur eines Systems von Kugeln (Scheiben) mit maximaler Verdichtung.
Allerdings haben Sandk rner eine Gr e von etwa einem Millimeter, w hrend Schlickk rner nur einige Zehntel Mikrometer gro sind und Tonk rner noch kleiner sind, im Bereich von nur wenigen Mikrometern.

Vergleich zwischen Sand-, Schluff- und Tonk rnern.
Dies bedeutet, dass ein Sandkorn etwa 300 Mal gr er ist als ein Schlickkorn und ungef hr 1000 Mal gr er als ein Tonkorn. Daher kann, wenn wir Ton oder Schlick zum Sand hinzuf gen, dieses Material die Zwischenr ume zwischen den Sandk rnern ausf llen:

Zwischenr ume zwischen den Sandk rnern, die mit Schluff- und Tonk rnern gef llt sind, oder Schluff, der mit Ton gef llt ist.
(ID 2079)
Im Fall von Kugeln wird eine optimale Anordnung erreicht, bei der der leere Raum im Verh ltnis zum Gesamtvolumen, was der optimalen Porosit t des Modells entspricht und die wir als die Eigene Porosität des Sandes ($q_a$) bezeichnen, in der Gr enordnung liegt:
$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$
Dieser Wert wurde im 17. Jahrhundert erstmals von Johannes Kepler vorgeschlagen und war als 'Keplers Vermutung' bekannt. Allerdings wurde er erst im Jahr 1998 von Thomas C. Hales bewiesen.
(ID 3172)
Im Fall von Schluff, der als kleine W rfel modelliert wird, entstehen auf dieser Ebene Kr fte zwischen den K rnern, die die Art und Weise, wie sie sich anordnen, verzerren. Aus diesem Grund gibt es keine optimalen Stapelungen von W rfeln bereinander, sondern eine Struktur, in die Eigene Porosität des Schlicks ($q_i$) eine ungef hre Gr enordnung von:
$q_i \sim \displaystyle\frac{1}{3}$
hat.
(ID 15079)
Im Fall von Ton, der als kleine Schichten modelliert wird, entstehen auf dieser Ebene Kr fte zwischen den K rnern, die die Art und Weise, wie sie sich anordnen, ver ndern. Aus diesem Grund gibt es keine optimalen Stapelungen von Schichten bereinander, sondern eher eine Struktur, in die Eigene Porosität des Schlicks ($q_i$) eine ungef hre Gr enordnung von:
$q_c\sim \displaystyle\frac{2}{5}$
hat.
(ID 15080)
Die Sedimentk rner im Boden k nnen zuf llig verteilt sein, was bedeutet, dass sie keine Konzentrationen eines bestimmten K rnertyps bilden. Dies w rde dazu f hren, dass Sand- und Schluffk rner aufgrund ihrer Gr e und Menge in einer Tonmatrix verteilt sind:

Homogene Verteilung der K rner.
Es besteht jedoch auch die M glichkeit, dass sie nach Typ gruppiert sind und es nur eine begrenzte Durchdringung gibt. Mit anderen Worten k nnten Tonk rner zumindest teilweise die R ume innerhalb einer getrennten Struktur aus Sand- und Schluffk rnern einnehmen:

Verteilung der K rner mit typspezifischen Konglomeraten.
Die Art und Weise, wie sich Boden absetzt, kann zu getrennten Schichten aus Sand, Schluff und Ton f hren. Auf der anderen Seite kann die Bewegung des Bodens zu Mischprozessen f hren.
(ID 925)
Wenn wir ein einzelnes Korn betrachten, k nnen wir sein individuelles Volumen, bezeichnet als $V_q$, und den Anteil im Gesamtvolumen $V$ unterscheiden, der dem Hohlraum (Porosit t) entspricht:

Dies impliziert, dass $1-q$ den Anteil des Volumens $V$ darstellt, der vom festen Volumen $V_q$ eingenommen wird. Daher gilt:
$V_q = (1-q)V$
Daher ist das Volumen, das mit einem Korn verbunden ist (festes Volumen und mit dem Korn verbundene Porosit t):
$V=\displaystyle\frac{1}{1-q}V_q$
Was hier in Bezug auf ein einzelnes Korn ausgedr ckt wird, gilt auch f r alle K rner innerhalb einer Komponente. Mit anderen Worten, wir k nnen $V_q$ als das feste Volumen der gesamten Komponente $q$ betrachten.
(ID 2075)
Die in der Kornstruktur vorhandene Porosit t bezieht sich auf eine Art von Porosit t, die mikroskopisch ist und als Prim rporosit t bekannt ist. Jedoch kann der Boden auch R ume enthalten, die sich aufgrund von Verformungen schlie en k nnen, sei es auf nat rliche Weise oder als Ergebnis externer Eingriffe.
Nat rliche Verformungen k nnen mit Trocknungsprozessen zusammenh ngen, die zu einer Volumenreduzierung und zur Bildung von Rissen f hren. Ein weiterer Mechanismus beinhaltet geologische Kr fte wie Erdbeben oder gravitationsbedingte Bewegungen. Auf der anderen Seite umfassen menschliche Eingriffe h ufige landwirtschaftliche Aktivit ten wie das Pfl gen und andere Erdbewegungsprozesse.
Wir werden diese durch Verformungen entstehenden R ume als der Makroporenvolumen ($V_m$) bezeichnen.
Diese Art von Porosit t kann direkt in einer Bodenprobe beobachtet werden. Im folgenden Beispiel gibt es drei Proben: eine mit einem hohen Anteil an Makroporen, eine weitere mit einigen Makroporen und die letzte praktisch ohne deren Vorhandensein:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004
(ID 2071)
Porosit t bezieht sich auf den leeren Raum innerhalb der Bodenstruktur. Es gibt jedoch zwei Arten von Porosit t: Mikro- und Makroporosit t. Der Unterschied besteht darin, dass die Mikroporosit t der Struktur der Bodenk rner inh rent ist und nicht ver ndert werden kann, ohne die Art und Weise zu beeinflussen, wie die K rner auf mikroskopischer Ebene gestapelt sind. Die zweite Art der Porosit t entsteht durch interne Prozesse oder die Art und Weise, wie der Boden manipuliert wird.
Daher gibt es zwei M glichkeiten, das Gesamtvolumen des Bodens aufzuschl sseln:
In Bezug auf die Makroporosit t:
der Makroporenvolumen ($V_m$): Makroporosit t, die unabh ngig von der mikroskopischen Bodenstruktur ist.
das Eigenvolumen ($V_z$): Das Volumen, das von den K rnern eingenommen wird, einschlie lich der Mikroporen, die beim Stapeln entstehen.
Basierend auf der Porosit t, unabh ngig von ihrer Herkunft:
der Porenvolumen ($V_p$): Porosit t, die im Allgemeinen unabh ngig von ihrer Herkunft ist.
das Solides Volumen ($V_s$): Das Volumen, das von den K rnern eingenommen wird, ohne die Mikroporosit t einzubeziehen, die beim Stapeln entsteht.
Diese Struktur kann wie folgt dargestellt werden:

(ID 15090)
(ID 15217)
ID:(361, 0)
