Usuario:


Porosidad en general
Storyboard

La formulación del modelo del suelo distingue entre tres materiales diferentes y sus proporciones relativas. Sin embargo, al considerar la forma en que los granos están dispuestos, es evidente que inevitablemente existen espacios entre ellos que deben ser descritos. Estos espacios son fundamentales, ya que el movimiento y la difusión del agua dependen de ellos. Por lo tanto, es necesario primero introducir el concepto de porosidad y establecer algunos criterios para su presencia, así como comprender cómo puede variar. Luego, podremos estudiar su efecto en el comportamiento del suelo.

>Modelo

ID:(361, 0)


Mecanismos
Concepto


ID:(15198, 0)


Porosidad de un sistema granular
Concepto

Si tienes un material granular, siempre habrá espacio entre los granos. Incluso en la forma más óptima de empaquetar los granos, siempre habrá un espacio que no se puede utilizar. En el caso de las esferas, la máxima compactación se logra cuando se agrupan tres de ellas y se coloca otra encima, formando una pirámide de base triangular. En este caso, se logra que el espacio no utilizado sea solo el 25%:



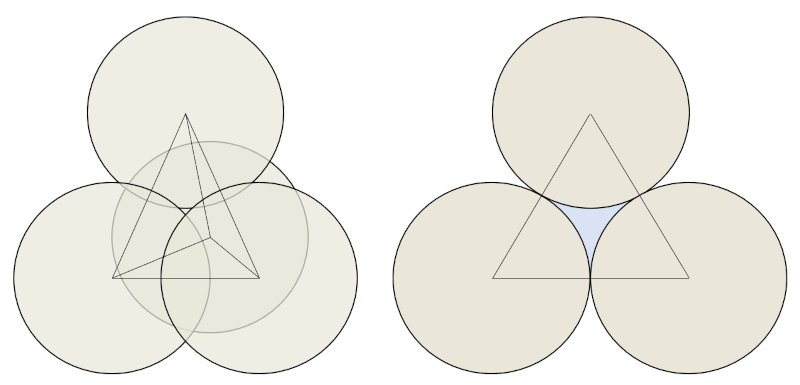
Para ilustrar mejor cómo se forman estos espacios, al lado de la pirámide de base triangular se muestra el caso en dos dimensiones, donde se ha resaltado en color celeste el espacio entre los granos.

Lo que aquí se observa como espacio entre algunos granos puede extrapolarse a toda la muestra completa. Por lo tanto, en una muestra de arena que se hace vibrar hasta que los granos se ordenan de manera óptima, se observa que un total del 25% del espacio queda vacío. A nivel macroscópico, esto se conoce como el volumen de los poros ($V_p$).

ID:(2072, 0)


Porosidad con granos de diferentes tamaños
Concepto

Como se mencionó anteriormente, si el suelo estuviera compuesto solo por granos de arena, tendríamos una estructura con espacios generados debido a la incapacidad de llenar completamente esos espacios:

Estructura base de un sistema de esferas (discos) con máxima compactación.



Sin embargo, los granos de arena tienen un tamaño del orden de un milímetro, mientras que el limo tiene solo unas decenas de micrones y los de arcilla son aún más pequeños, en el rango de unos pocos micrones.

Comparación entre los granos de arena, limo y arcilla.



Esto significa que un grano de arena es aproximadamente 300 veces más grande que un grano de limo y aproximadamente 1000 veces más grande que un grano de arcilla. Por lo tanto, si agregamos arcilla o limo a la arena, este material podrá llenar los espacios entre los granos:

Espacios entre los granos de arena llenados con granos de limo y arcilla, o de limo llenando con arcilla.

ID:(2079, 0)


Porosidad mínima de la arena
Variable

En el caso de las esferas, se logra una disposición óptima en la que el espacio vacío en relación al volumen total, que corresponde a la porosidad óptima del modelo, la cual denominaremos como la porosidad propia de la arena ($q_a$), tiene un valor del orden de:

$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$

Este valor fue propuesto inicialmente en el siglo XVII por Johannes Kepler y se conoció como la 'conjetura de Kepler'. Sin embargo, no fue demostrado hasta 1998 por Thomas C. Hales.

ID:(3172, 0)


Porosidad mínima del limo
Variable

En el caso del limo, que se modela como cubos de pequeño tamaño, surgen fuerzas entre los granos a esta escala que distorsionan la forma en que se ordenan. Por esta razón, no existen apilamientos óptimos de cubos uno sobre otro, sino una estructura en la que la porosidad propia del limo ($q_i$) tiene un orden de magnitud aproximado de:

$q_i \sim \displaystyle\frac{1}{3}$

.

ID:(15079, 0)


Porosidad mínima de arcilla
Variable

En el caso de la arcilla, que se modela como láminas de pequeño tamaño, surgen fuerzas entre los granos a esta escala que modifican la forma en la que se organizan. Por esta razón, no existen apilamientos óptimos de láminas una sobre otra, sino más bien una estructura en la que la porosidad propia del limo ($q_i$) tiene un orden de magnitud aproximado de:

$q_c\sim \displaystyle\frac{2}{5}$

.

ID:(15080, 0)


Distribución de granos de suelo
Concepto

Los granos de suelo pueden estar distribuidos de manera aleatoria, es decir, no formar concentraciones de un tipo de grano en particular. Esto llevaría a que los granos de arena y limo, debido a su tamaño y número, estén dispersos en una matriz de arcilla:

Distribución homogénea de granos.



Sin embargo, existe la posibilidad de que estén agrupados por tipo y que haya una penetración limitada. En otras palabras, los granos de arcilla pueden ocupar, al menos parcialmente, los espacios en una estructura de granos de arena y limo de manera separada:

Distribución de granos con conglomerados específicos por tipo.

La sedimentación del suelo puede dar lugar a capas de arena, limo y arcilla, cada una por separado. Por otro lado, el movimiento del suelo puede desencadenar procesos de mezcla.

ID:(925, 0)


Cálculo de volumen por componente
Concepto

Si consideramos un grano, podemos distinguir su volumen propio $V_q$ y la fracción en el volumen total $V$ que corresponde al espacio vacío (porosidad):



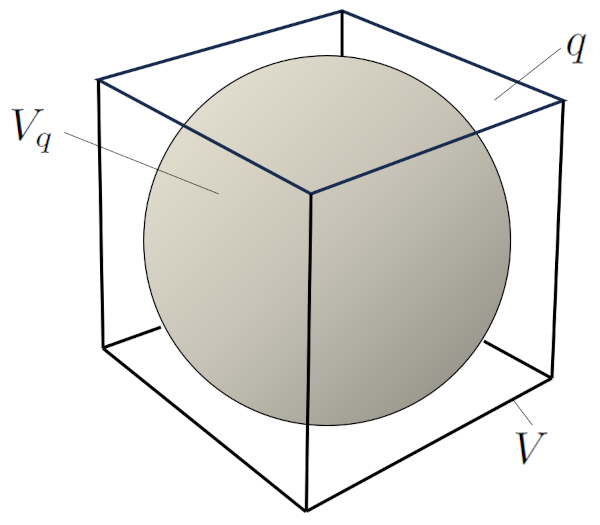
Esto significa que $1-q$ corresponde a la fracción del volumen $V$ que ocupa el volumen sólido $V_q$. Por lo tanto,

$V_q = (1-q)V$



Por lo tanto, el volumen que corresponde a un grano (volumen sólido y porosidad asociada al grano) es

$V=\displaystyle\frac{1}{1-q}V_q$

Lo que se expresa aquí con respecto a un grano también se aplica a todos los granos de un componente. Es decir, podemos considerar $V_q$ como el volumen sólido de toda la componente $q$.

ID:(2075, 0)


Volumen de macroporos
Concepto

La porosidad inherente a la estructura de los granos se refiere a un tipo de porosidad que es microscópica y se conoce como porosidad primaria. Sin embargo, el suelo también puede contener espacios que pueden cerrarse debido a deformaciones, ya sea de forma natural o como resultado de intervenciones externas.

Las deformaciones naturales pueden estar relacionadas con procesos de secado que provocan una reducción de volumen y la formación de grietas. Otro mecanismo implica fuerzas geológicas como sismos o movimientos inducidos por la gravedad. Por otro lado, las intervenciones humanas incluyen actividades agrícolas comunes como el arado y otros procesos de movimiento de tierra.

A estos espacios resultantes de las deformaciones los llamaremos el volumen de los macroporos ($V_m$).

Este tipo de porosidad se puede observar directamente en una muestra de suelo. En el siguiente ejemplo, se muestra una muestra con un alto contenido de macroporos, otra con algunos macroporos, y una última prácticamente sin presencia de ellos:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004

ID:(2071, 0)


Modelos volumen y porosidad
Concepto

La porosidad se refiere al espacio vacío dentro de la estructura del suelo. Sin embargo, existen dos tipos de porosidad: micro y macro porosidad. La diferencia radica en que la primera es inherente a la estructura de los granos del suelo y no se puede modificar sin afectar la forma en que se apilan los granos a nivel microscópico. La segunda es la porosidad que se genera por procesos internos o por la forma en que se manipula el suelo.

En consecuencia, existen dos formas de desglosar el volumen total del suelo:

En función de la macroporosidad:

• el volumen de los macroporos ($V_m$): Macroporosidad que no depende de la estructura microscópica del suelo.
• el volumen propio ($V_z$): Volumen propio de los granos, incluyendo los microporos que se generan al apilarlos.

En función de la porosidad independiente de su origen:

• el volumen de los poros ($V_p$): Porosidad en general independiente de su origen.
• el volumen sólido ($V_s$): Volumen propio de los granos sin incluir la microporosidad generada al apilarlos.

Esta estructura se puede representar de la siguiente manera:

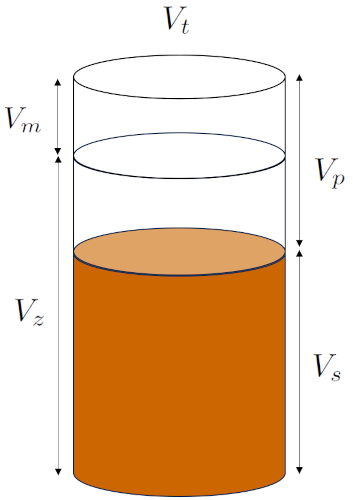
ID:(15090, 0)


Modelo
Concepto


ID:(15217, 0)


Porosidad en general
Modelo

La formulación del modelo del suelo distingue entre tres materiales diferentes y sus proporciones relativas. Sin embargo, al considerar la forma en que los granos están dispuestos, es evidente que inevitablemente existen espacios entre ellos que deben ser descritos. Estos espacios son fundamentales, ya que el movimiento y la difusión del agua dependen de ellos. Por lo tanto, es necesario primero introducir el concepto de porosidad y establecer algunos criterios para su presencia, así como comprender cómo puede variar. Luego, podremos estudiar su efecto en el comportamiento del suelo.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$g_c$
g_c
Fracción de masa de arcilla en la muestra
-
$g_a$
g_a
Fracción de masa de arena en la muestra
-
$g_i$
g_i
Fracción de masa de limo en la muestra
-
$f$
f
Porosidad
-
$q_c$
q_c
Porosidad propia de la arcilla
-
$q_a$
q_a
Porosidad propia de la arena
-
$q_i$
q_i
Porosidad propia del limo
-
$V_m$
V_m
Volumen de los macroporos
m^3
$V_p$
V_p
Volumen de los poros
m^3
$V_z$
V_z
Volumen propio
m^3
$V_s$
V_s
Volumen sólido
m^3
$V_c$
V_c
Volumen sólido de arcilla
m^3
$V_a$
V_a
Volumen sólido de arena
m^3
$V_i$
V_i
Volumen sólido de limo
m^3
$V_s$
V_s
Volumen sólido de una componente
m^3
$V_t$
V_t
Volumen total
m^3

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

La porosidad propia de la arena ($q_a$) representa la fracci n del volumen $V$ que corresponde a los espacios vac os entre los granos de arena. Por lo tanto, $1-q_a$ es la fracci n de el volumen sólido de arena ($V_a$) en relaci n a $V$:

$1 - q_a = \displaystyle\frac{V_a}{V}$



De esta manera, el volumen ocupado por los granos de arena es:

$\displaystyle\frac{V_a}{1 - q_a}$



An logamente, para el limo, utilizamos la porosidad propia del limo ($q_i$) y el volumen sólido de limo ($V_i$), por lo que el volumen ocupado por los granos de limo es:

$\displaystyle\frac{V_i}{1 - q_i}$



Y para la arcilla, empleamos la porosidad propia de la arcilla ($q_c$) y el volumen sólido de arcilla ($V_c$). Por lo tanto, el volumen ocupado por los granos de arcilla es:

$\displaystyle\frac{V_c}{1 - q_c}$



En resumen, el volumen total es la suma de estos vol menes, es decir,

$ V_z = \displaystyle\frac{1}{1- q_a } V_a + \displaystyle\frac{1}{1- q_i } V_i + \displaystyle\frac{1}{1- q_c } V_c $

(ID 2077)

Con el volumen total ($V_t$) expresado en t rminos de el volumen de los macroporos ($V_m$) y el volumen propio ($V_z$) con

$ V_t = V_m + V_z $



y considerando el volumen sólido ($V_s$) y el volumen de los poros ($V_p$), llegamos a

$ V_t = V_s + V_p $



lo que nos conduce a la ecuaci n

$V_m + V_z = V_s + V_p$



y, por lo tanto,

$ V_p = V_m + V_z - V_s $

(ID 10556)

Si se dispone de la porosidad ($f$) seg n la ecuaci n:

$ f =\displaystyle\frac{ V_p }{ V_t }$



y del el volumen sólido ($V_s$) mediante la ecuaci n:

$ V_t = V_s + V_p $



se puede eliminar el volumen total ($V_t$) y obtener el volumen de los poros ($V_p$) de la siguiente manera:

$ V_p =\displaystyle\frac{ f }{1- f } V_s $

(ID 10590)

El volumen de los poros ($V_p$) puede calcularse utilizando el volumen de los macroporos ($V_m$), el volumen propio ($V_z$), y el volumen sólido ($V_s$) a trav s de la ecuaci n

$ V_p = V_m + V_z - V_s $



donde el volumen sólido ($V_s$) se calcula mediante el volumen sólido de arena ($V_a$), el volumen sólido de limo ($V_i$), y el volumen sólido de arcilla ($V_c$) seg n

$ V_s = V_a + V_l + V_c $



y se utiliza la relaci n

$ V_z = \displaystyle\frac{1}{1- q_a } V_a + \displaystyle\frac{1}{1- q_i } V_i + \displaystyle\frac{1}{1- q_c } V_c $



para obtener con la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$) y la porosidad propia de la arcilla ($q_c$)

$ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $

(ID 15081)

Ejemplos


(ID 15198)

Si tienes un material granular, siempre habr espacio entre los granos. Incluso en la forma m s ptima de empaquetar los granos, siempre habr un espacio que no se puede utilizar. En el caso de las esferas, la m xima compactaci n se logra cuando se agrupan tres de ellas y se coloca otra encima, formando una pir mide de base triangular. En este caso, se logra que el espacio no utilizado sea solo el 25%:



Para ilustrar mejor c mo se forman estos espacios, al lado de la pir mide de base triangular se muestra el caso en dos dimensiones, donde se ha resaltado en color celeste el espacio entre los granos.

Lo que aqu se observa como espacio entre algunos granos puede extrapolarse a toda la muestra completa. Por lo tanto, en una muestra de arena que se hace vibrar hasta que los granos se ordenan de manera ptima, se observa que un total del 25% del espacio queda vac o. A nivel macrosc pico, esto se conoce como el volumen de los poros ($V_p$).

(ID 2072)

Como se mencion anteriormente, si el suelo estuviera compuesto solo por granos de arena, tendr amos una estructura con espacios generados debido a la incapacidad de llenar completamente esos espacios:

Estructura base de un sistema de esferas (discos) con m xima compactaci n.



Sin embargo, los granos de arena tienen un tama o del orden de un mil metro, mientras que el limo tiene solo unas decenas de micrones y los de arcilla son a n m s peque os, en el rango de unos pocos micrones.

Comparaci n entre los granos de arena, limo y arcilla.



Esto significa que un grano de arena es aproximadamente 300 veces m s grande que un grano de limo y aproximadamente 1000 veces m s grande que un grano de arcilla. Por lo tanto, si agregamos arcilla o limo a la arena, este material podr llenar los espacios entre los granos:

Espacios entre los granos de arena llenados con granos de limo y arcilla, o de limo llenando con arcilla.

(ID 2079)

En el caso de las esferas, se logra una disposici n ptima en la que el espacio vac o en relaci n al volumen total, que corresponde a la porosidad ptima del modelo, la cual denominaremos como la porosidad propia de la arena ($q_a$), tiene un valor del orden de:

$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$

Este valor fue propuesto inicialmente en el siglo XVII por Johannes Kepler y se conoci como la 'conjetura de Kepler'. Sin embargo, no fue demostrado hasta 1998 por Thomas C. Hales.

(ID 3172)

En el caso del limo, que se modela como cubos de peque o tama o, surgen fuerzas entre los granos a esta escala que distorsionan la forma en que se ordenan. Por esta raz n, no existen apilamientos ptimos de cubos uno sobre otro, sino una estructura en la que la porosidad propia del limo ($q_i$) tiene un orden de magnitud aproximado de:

$q_i \sim \displaystyle\frac{1}{3}$

.

(ID 15079)

En el caso de la arcilla, que se modela como l minas de peque o tama o, surgen fuerzas entre los granos a esta escala que modifican la forma en la que se organizan. Por esta raz n, no existen apilamientos ptimos de l minas una sobre otra, sino m s bien una estructura en la que la porosidad propia del limo ($q_i$) tiene un orden de magnitud aproximado de:

$q_c\sim \displaystyle\frac{2}{5}$

.

(ID 15080)

Los granos de suelo pueden estar distribuidos de manera aleatoria, es decir, no formar concentraciones de un tipo de grano en particular. Esto llevar a a que los granos de arena y limo, debido a su tama o y n mero, est n dispersos en una matriz de arcilla:

Distribuci n homog nea de granos.



Sin embargo, existe la posibilidad de que est n agrupados por tipo y que haya una penetraci n limitada. En otras palabras, los granos de arcilla pueden ocupar, al menos parcialmente, los espacios en una estructura de granos de arena y limo de manera separada:

Distribuci n de granos con conglomerados espec ficos por tipo.

La sedimentaci n del suelo puede dar lugar a capas de arena, limo y arcilla, cada una por separado. Por otro lado, el movimiento del suelo puede desencadenar procesos de mezcla.

(ID 925)

Si consideramos un grano, podemos distinguir su volumen propio $V_q$ y la fracci n en el volumen total $V$ que corresponde al espacio vac o (porosidad):



Esto significa que $1-q$ corresponde a la fracci n del volumen $V$ que ocupa el volumen s lido $V_q$. Por lo tanto,

$V_q = (1-q)V$



Por lo tanto, el volumen que corresponde a un grano (volumen s lido y porosidad asociada al grano) es

$V=\displaystyle\frac{1}{1-q}V_q$

Lo que se expresa aqu con respecto a un grano tambi n se aplica a todos los granos de un componente. Es decir, podemos considerar $V_q$ como el volumen s lido de toda la componente $q$.

(ID 2075)

La porosidad inherente a la estructura de los granos se refiere a un tipo de porosidad que es microsc pica y se conoce como porosidad primaria. Sin embargo, el suelo tambi n puede contener espacios que pueden cerrarse debido a deformaciones, ya sea de forma natural o como resultado de intervenciones externas.

Las deformaciones naturales pueden estar relacionadas con procesos de secado que provocan una reducci n de volumen y la formaci n de grietas. Otro mecanismo implica fuerzas geol gicas como sismos o movimientos inducidos por la gravedad. Por otro lado, las intervenciones humanas incluyen actividades agr colas comunes como el arado y otros procesos de movimiento de tierra.

A estos espacios resultantes de las deformaciones los llamaremos el volumen de los macroporos ($V_m$).

Este tipo de porosidad se puede observar directamente en una muestra de suelo. En el siguiente ejemplo, se muestra una muestra con un alto contenido de macroporos, otra con algunos macroporos, y una ltima pr cticamente sin presencia de ellos:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004

(ID 2071)

La porosidad se refiere al espacio vac o dentro de la estructura del suelo. Sin embargo, existen dos tipos de porosidad: micro y macro porosidad. La diferencia radica en que la primera es inherente a la estructura de los granos del suelo y no se puede modificar sin afectar la forma en que se apilan los granos a nivel microsc pico. La segunda es la porosidad que se genera por procesos internos o por la forma en que se manipula el suelo.

En consecuencia, existen dos formas de desglosar el volumen total del suelo:

En funci n de la macroporosidad:

• el volumen de los macroporos ($V_m$): Macroporosidad que no depende de la estructura microsc pica del suelo.
• el volumen propio ($V_z$): Volumen propio de los granos, incluyendo los microporos que se generan al apilarlos.

En funci n de la porosidad independiente de su origen:

• el volumen de los poros ($V_p$): Porosidad en general independiente de su origen.
• el volumen sólido ($V_s$): Volumen propio de los granos sin incluir la microporosidad generada al apilarlos.

Esta estructura se puede representar de la siguiente manera:

(ID 15090)


(ID 15217)

ID:(361, 0)