Storyboard

The formulation of the soil model distinguishes three different materials and their relative proportions. However, considering the way grains are arranged, it becomes apparent that there are inevitably spaces between them that need to be described. These spaces are crucial since the movement and diffusion of water depend on them. Therefore, it is necessary to first introduce the concept of porosity and establish criteria for its presence, as well as understand how it can vary. Subsequently, we can study its effect on soil behavior.

>Model

ID:(361, 0)

Concept

>Top

ID:(15198, 0)

Concept

>Top

If you have a granular material, there will always be space between the grains. Even in the most optimal way of packing the grains, there will always be some space that cannot be utilized. In the case of spheres, maximum compaction is achieved when three of them are grouped together with another one placed on top, forming a triangular base pyramid. In this case, the unused space is reduced to only 25%:

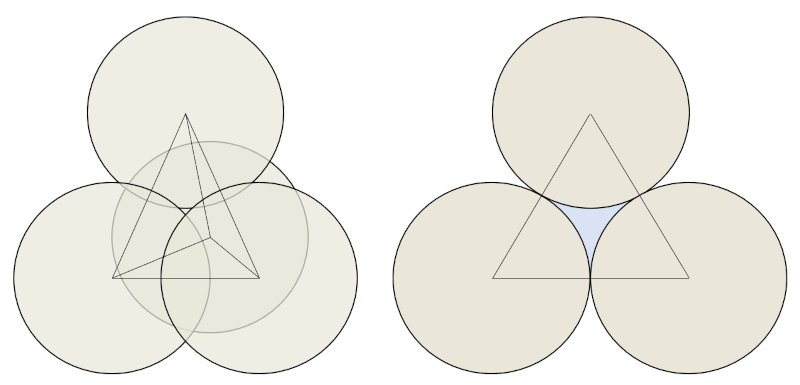
To better illustrate how these spaces form, next to the triangular base pyramid, we show a two-dimensional case where the space between the grains has been highlighted in blue.

What is observed here as space between some grains can be extrapolated to the entire sample. Therefore, in a sample of sand that is vibrated until the grains are optimally arranged, it is observed that a total of 25% of the space remains vacant. At a macroscopic level, this is known as the pore volume ($V_p$).

ID:(2072, 0)

Concept

>Top

As mentioned earlier, if the soil were composed solely of sand grains, we would have a structure with spaces generated due to the inability to completely fill those spaces:

Basic structure of a sphere (disk) system with maximum compactness.

However, sand grains are around a millimeter in size, while silt grains are only a few tens of microns, and clay grains are even smaller, in the range of just a few microns.

Comparison between sand, silt, and clay grains.

This means that a sand grain is approximately 300 times larger than a silt grain and roughly 1000 times larger than a clay grain. Therefore, if we add clay or silt to the sand, this material can occupy the spaces between the sand grains:

Gaps between sand grains filled with silt and clay, or silt filled with clay.

ID:(2079, 0)

Variable

>Top

In the case of spheres, an optimal arrangement is achieved where the empty space in relation to the total volume, corresponding to the optimal porosity of the model we'll refer to as the sand's own porosity ($q_a$), is of the order:

$q_a = 1-\displaystyle\frac{ \pi }{3\sqrt{2}} \sim 0.25$

This value was initially proposed in the 17th century by Johannes Kepler and was known as 'Kepler's conjecture'. However, it was only proven in 1998 by Thomas C. Hales.

ID:(3172, 0)

Variable

>Top

In the case of silt, which is modeled as small cubes, forces emerge between the grains at this scale that distort the way they arrange themselves. For this reason, there are no optimal stackings of cubes on top of each other, but rather a structure in which the silt own porosity ($q_i$) has an approximate order of magnitude of:

$q_i \sim \displaystyle\frac{1}{3}$

.

ID:(15079, 0)

Variable

>Top

In the case of clay, which is modeled as small sheets, forces emerge between the grains at this scale that alter the way they arrange themselves. For this reason, there are no optimal stackings of sheets on top of each other, but rather a structure in which the silt own porosity ($q_i$) has an approximate order of magnitude of:

$q_c\sim \displaystyle\frac{2}{5}$

.

ID:(15080, 0)

Concept

>Top

Sediment grains in soil can be distributed randomly, meaning they do not form concentrations of a particular grain type. This would result in sand and silt grains, due to their size and quantity, being dispersed within a clay matrix:

Homogeneous distribution of grains.

However, there is also the possibility that they may be grouped by type with limited interpenetration. In other words, clay grains could occupy at least some of the spaces within a separate structure of sand and silt grains:

Distribution of grains with type-specific conglomerates.

The way soil settles can lead to separate layers of sand, silt, and clay. On the other hand, soil movement can result in mixing processes.

ID:(925, 0)

Concept

>Top

If we consider a single grain, we can distinguish its individual volume, denoted as $V_q$, and the fraction within the total volume $V$ that corresponds to the void space (porosity):

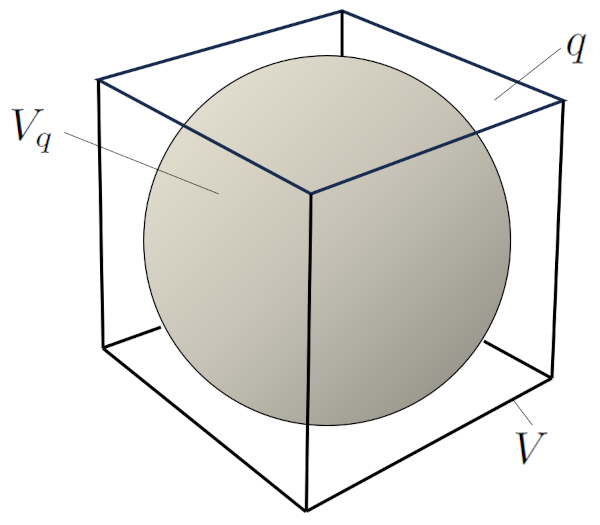
This implies that $1-q$ represents the fraction of volume $V$ occupied by the solid volume $V_q$. Therefore,

$V_q = (1-q)V$

Hence, the volume associated with a grain (solid volume and porosity associated with the grain) is

$V=\displaystyle\frac{1}{1-q}V_q$

What is expressed here with respect to a single grain also holds true for all the grains within a component. In other words, we can consider $V_q$ as the solid volume of the entire component $q$.

ID:(2075, 0)

Concept

>Top

The porosity inherent to the grain structure refers to a type of porosity that is microscopic and is known as primary porosity. However, soil can also contain spaces that can close due to deformations, either naturally or as a result of external interventions.

Natural deformations can be related to drying processes that result in a volume reduction and the formation of cracks. Another mechanism involves geological forces such as earthquakes or gravity-induced movements. On the other hand, human interventions include common agricultural activities such as plowing and other earthmoving processes.

We will refer to these spaces resulting from deformations as the macropore volume ($V_m$).

This type of porosity can be directly observed in a soil sample. In the following example, there are three samples: one with a high content of macropores, another with some macropores, and the last one with practically no presence of them:

Visual Soil assessment, Beata Houskova, 2nd European Summer School on Soil Survey 12-16 June 2004

ID:(2071, 0)

Concept

>Top

Porosity refers to the empty space within the soil structure. However, there are two types of porosity: micro and macro porosity. The difference is that micro porosity is inherent to the soil grain structure and cannot be altered without affecting how the grains stack at a microscopic level. The second type of porosity is generated by internal processes or how the soil is manipulated.

As a result, there are two ways to break down the total volume of soil:

Based on macroporosity:

• the macropore volume ($V_m$): Macroporosity that is independent of the microscopic soil structure.
• the own volume ($V_z$): The volume occupied by the grains, including the micropores generated when they are stacked.

Based on porosity regardless of its origin:

• the pore volume ($V_p$): Porosity that is generally independent of its origin.
• the solid volume ($V_s$): The volume occupied by the grains, excluding the microporosity generated when they are stacked.

This structure can be represented as follows:

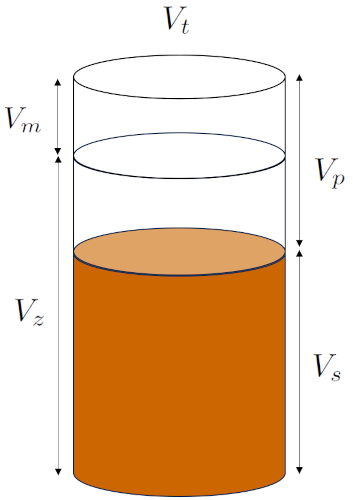
ID:(15090, 0)

Concept

>Top

Selected parameter

Calculations

ID:(15217, 0)

Equation

>Top, >Model

The own volume ($V_z$) is defined in terms of the solid volume of sand ($V_a$), the solid volume of silt ($V_i$), and the solid volume of clay ($V_c$), including the sand's own porosity ($q_a$), the silt own porosity ($q_i$), and the clay own porosity ($q_c$), as follows:

$ V_z = \displaystyle\frac{1}{1- q_a } V_a + \displaystyle\frac{1}{1- q_i } V_i + \displaystyle\frac{1}{1- q_c } V_c $

Conditions

Variables

$q_c$

Mass fraction of clay in the sample

$-$

$q_a$

Mass fraction of sand in the sample

$-$

$q_i$

Mass fraction of silt in the sample

$-$

$V_z$

Own volume

$m^3$

$V_c$

Solid volume of clay

$m^3$

$V_a$

Solid volume of sand

$m^3$

$V_i$

Solid volume of silt

$m^3$

Relation

Development

The sand's own porosity ($q_a$) represents the fraction of volume $V$ that corresponds to the empty spaces between the sand grains. Therefore, $1-q_a$ is the fraction of the solid volume of sand ($V_a$) with respect to $V$:

$1 - q_a = \displaystyle\frac{V_a}{V}$

Consequently, the volume occupied by the sand grains is:

$\displaystyle\frac{V_a}{1 - q_a}$

Similarly, for silt, we use the silt own porosity ($q_i$) and the solid volume of silt ($V_i$), so the volume occupied by the silt grains is:

$\displaystyle\frac{V_i}{1 - q_i}$

And for clay, we use the clay own porosity ($q_c$) and the solid volume of clay ($V_c$). Hence, the volume occupied by the clay grains is:

$\displaystyle\frac{V_c}{1 - q_c}$

In summary, the total volume is the sum of these volumes, that is,

$ V_z = \displaystyle\frac{1}{1- q_a } V_a + \displaystyle\frac{1}{1- q_i } V_i + \displaystyle\frac{1}{1- q_c } V_c $

ID:(2077, 0)

Equation

>Top, >Model

The total volume ($V_t$) is the sum of the own volume ($V_z$), which includes the micropores given by the grain geometry, and the macropore volume ($V_m$), so that:

$ V_t = V_m + V_z $

Conditions

Variables

$V_m$

Macropore volume

$m^3$

$V_z$

Own volume

$m^3$

$V_t$

Total volume

$m^3$

Relation

ID:(15085, 0)

Equation

>Top, >Model

The total volume ($V_t$) is the sum of the pore volume ($V_p$), which includes both the micropores and the macropores in the soil, and the total Dry Mass of Sample ($M_s$), so that:

$ V_t = V_s + V_p $

Conditions

Variables

$V_p$

Pore volume

$m^3$

$V_s$

Solid volume of a component

$m^3$

$V_t$

Total volume

$m^3$

Relation

ID:(4726, 0)

Equation

>Top, >Model

When the two equations for calculating the total volume ($V_t$) are equated, a relationship for calculating the pore volume ($V_p$) in terms of the macropore volume ($V_m$), the own volume ($V_z$), and the solid volume ($V_s$) is obtained as follows:

$ V_p = V_m + V_z - V_s $

Conditions

Variables

$V_m$

Macropore volume

$m^3$

$V_z$

Own volume

$m^3$

$V_p$

Pore volume

$m^3$

$V_s$

Solid volume

$m^3$

Relation

Development

With the total volume ($V_t$) expressed in terms of the macropore volume ($V_m$) and the own volume ($V_z$) as

$ V_t = V_m + V_z $

and considering the solid volume ($V_s$) and the pore volume ($V_p$), we obtain

$ V_t = V_s + V_p $

which leads us to the equation

$V_m + V_z = V_s + V_p$

and, therefore,

$ V_p = V_m + V_z - V_s $

ID:(10556, 0)

Equation

>Top, >Model

In the case of clayey soil, sand and silt grains are distributed within a clay matrix. Consequently, the sand and silt grains do not contribute to porosity, unlike clay, which does so based on its intrinsic property the volume fraction of clay in the sample ($f_c$). Therefore, the the pore volume ($V_p$) comprises the macropore volume ($V_m$), the clay own porosity ($q_c$), and also the the solid volume of clay ($V_c$):

$ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $

Conditions

Variables

$q_c$

Clay own porosity

$-$

$V_m$

Macropore volume

$m^3$

$V_p$

Pore volume

$m^3$

$q_a$

Sand's own porosity

$-$

$q_i$

Silt own porosity

$-$

$V_c$

Solid volume of clay

$m^3$

$V_a$

Solid volume of sand

$m^3$

$V_i$

Solid volume of silt

$m^3$

Relation

Development

The pore volume ($V_p$) can be calculated using the macropore volume ($V_m$), the own volume ($V_z$), and the solid volume ($V_s$) through the equation

$ V_p = V_m + V_z - V_s $

where the solid volume ($V_s$) is calculated using the solid volume of sand ($V_a$), the solid volume of silt ($V_i$), and the solid volume of clay ($V_c$) as per

$ V_s = V_a + V_l + V_c $

and the relationship

$ V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$

is used to obtain

$ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $

ID:(15081, 0)

Equation

>Top, >Model

The porosity ($f$) expresses the relationship between the pore volume ($V_p$) and the total volume ($V_t$), allowing us to define the equation as follows:

$ f =\displaystyle\frac{ V_p }{ V_t }$

Conditions

Variables

$V_p$

Pore volume

$m^3$

$f$

Porosity

$-$

$V_t$

Total volume

$m^3$

Relation

ID:(4245, 0)

Equation

>Top, >Model

The pore volume ($V_p$) can be represented using the porosity ($f$):

and the volume of the pores is calculated from the solid volume ($V_s$) as follows:

$ V_p =\displaystyle\frac{ f }{1- f } V_s $

Conditions

Variables

$V_p$

Pore volume

$m^3$

$f$

Porosity

$-$

$V_s$

Solid volume

$m^3$

Relation

Development

If you have the porosity ($f$) as given by:

$ f =\displaystyle\frac{ V_p }{ V_t }$

and the solid volume ($V_s$) obtained through:

$ V_t = V_s + V_p $

you can eliminate the total volume ($V_t$) and obtain the pore volume ($V_p$) as follows:

$ V_p =\displaystyle\frac{ f }{1- f } V_s $

ID:(10590, 0)