Storyboard

Models are expressed in the form of networks of equations where the different nodes represent the variables of the system.

One of the challenges when solving problems in physics is that only equations valid for the existing conditions of the problem being analyzed can be employed. The model itself is defined based on all equations that are valid for the studied situation. Hence, the use of the model ensures that only equations corresponding to the situation being studied are employed.

By forming the different equations of the model using its variables, a network is established to determine the strategy for problem resolution. This network allows for the direct identification of intermediate variables that can be calculated, thus defining the necessary variables and the order in which intermediate variables should be calculated until the desired variables are obtained.

Ultimately, the risks of calculation errors are reduced by selecting the appropriate model and associating the given parameters with the variables of the model.

>Model

ID:(1932, 0)

Image

>Top

The equation of the path traveled

$\Delta s = s - s_0$

It can be represented as a (celestial) node associated to the nodes of the path traveled variable $\Delta s$, the initial position $s_0$ and the final position:

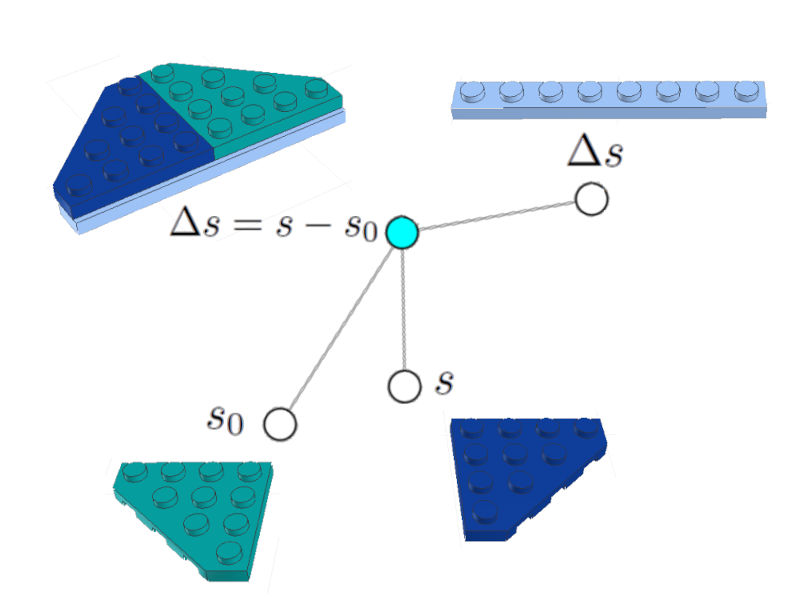
Equation of the path traveled

Images of the LEGO bricks including the representation of the equation are included.

ID:(14379, 0)

Image

>Top

The Elapsed Time Equation

$\Delta t = t - t_0$

It can be represented as a (celestial) node associated to the nodes of the variable of the elapsed time $\Delta t$, the initial time $t_0$ and the final time:

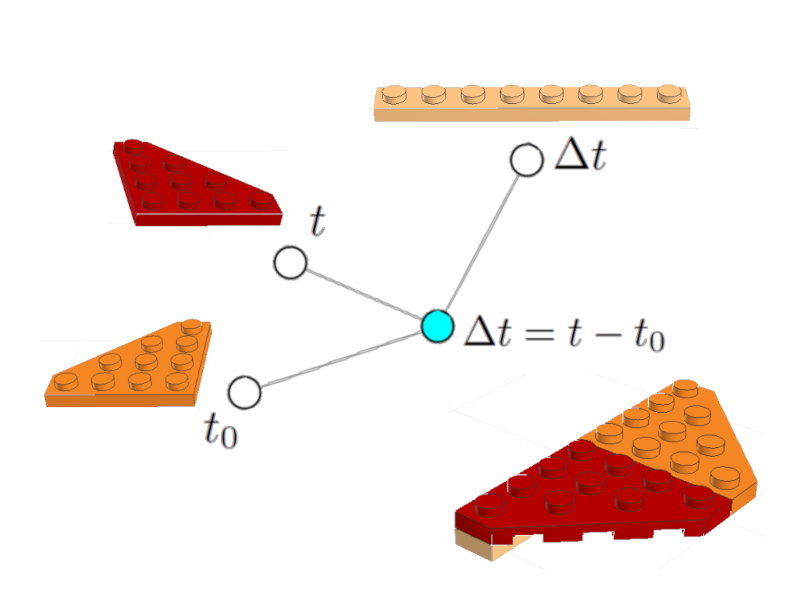
Elapsed time equation

Images of the LEGO bricks including the representation of the equation are included.

ID:(14380, 0)

Image

>Top

The speed equation

$v = \displaystyle\frac{\Delta s}{\Delta t}$

It can be represented as a (celestial) node associated to the nodes of the velocity variable $v$, the path traveled $\Delta s$ and the elapsed time $\Delta t$:

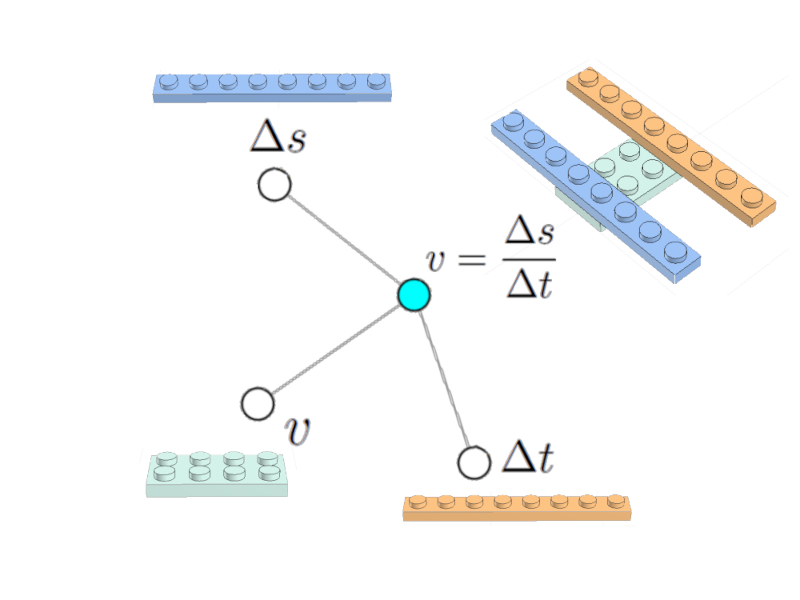
Speed equation

Images of the LEGO bricks including the representation of the equation are included.

ID:(14381, 0)

Image

>Top

With the three equations already entered, a fourth equation can be established that allows the position to be calculated at all times

$s = s_0 + v(t - t_0)$

which can also be represented as a (celestial) node associated to the nodes of the variable position $s$, initial position $s_0$, velocity $v$, initial time $t_0$ and final time $t$:

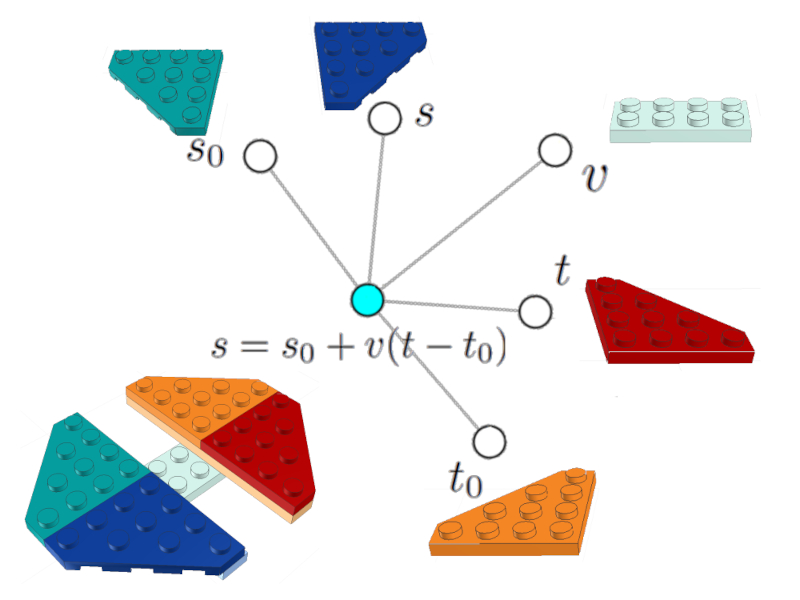
Position equation

Images of the LEGO bricks including the representation of the equation are included.

ID:(14382, 0)

Image

>Top

If all the equations are drawn with their respective graphs, it is seen that there are common variables that can be integrated.

It is important that each variable appears only once represented by its node (white)

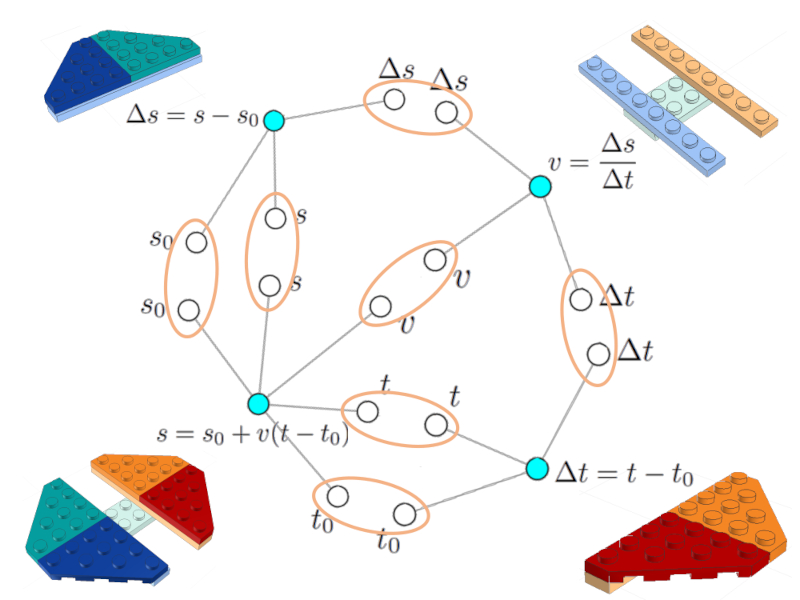
Forming the network

ID:(14383, 0)

Image

>Top

Once the common variables are integrated, the network that represents the model is obtained.

In this case, the model is simple, it only consists of 4 equations (celestial nodes) linked to each other by 7 variables (white nodes).

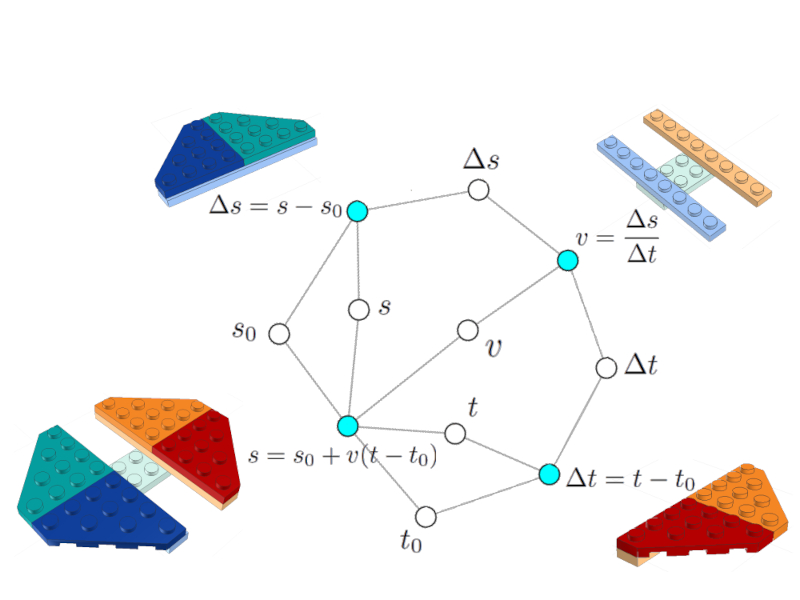
The model network

A more complex model may have multiple equations and variables. All of them linked forming a single network.

ID:(14384, 0)

Image

>Top

In principle, every variable in the model can be calculated. In this particular case:

If we take in case of the time we are going to arrive, we can mark the corresponding node in the model network with red:

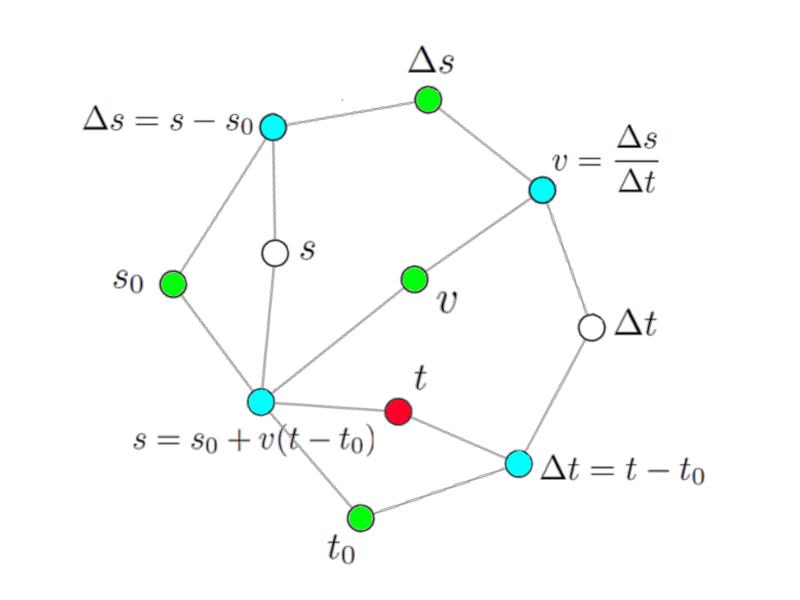
The model network for calculating the arrival time.

Consulting the network we immediately observe the associated nodes that correspond to the equations that can be used to calculate said variable. In this case they were marked in blue and correspond to the equations

$s = s_0 + v(t - t_0)$

and

$\Delta t = t - t_0$

ID:(14385, 0)

Image

>Top

To calculate a particular variable, we must first determine the variables whose values we are given.

To facilitate the interpretation, the nodes of the given variables can be marked with another color (light green).

The network of the model with the given variables and the variable to calculate.

In this way it is easy to see that the chosen variable cannot be calculated since both associated equations present variables for which we do not know their values (white nodes).

The general rule is

A variable (white node) can only be calculated if all other nodes associated with an equation (light blue node) are given (light green nodes). In general there cannot be more than one white node.

ID:(14386, 0)

Image

>Top

The searched variable (red node) cannot be calculated because in both associated equations there are other unknown variables (white nodes).

However, it is possible to calculate these using other network equations. For this we take, for example, the variable $s$ that can be calculated with the equation of the path traveled:

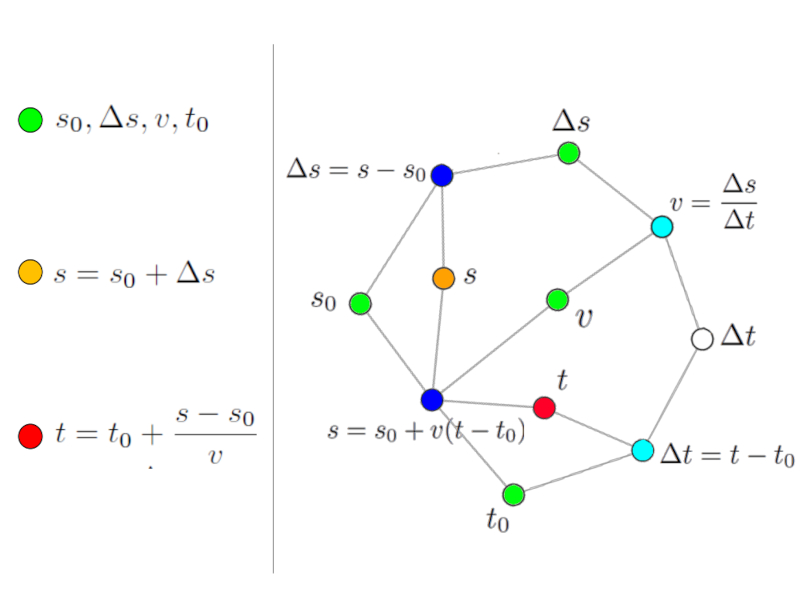
Solution via the intermediate variable final position.

Every time we identify an equation that has only one unknown (white or red node) we can use that equation to calculate that value. To facilitate the interpretation we can give a color to the calculated variable (orange).

In this way we can generalize the rule:

A variable (white or red node) can only be calculated with an equation (light blue node) if all other variables are known (light green or orange nodes).

The variable calculated in addition to the search variable is called the intermediate variable.

ID:(14387, 0)

Image

>Top

The searched variable (red node) cannot be calculated because in both associated equations there are other unknown variables (white nodes).

However, it is possible to calculate these using other network equations. For this we take, for example, the variable $\Delta t$ that can be calculated with the equation of the path traveled:

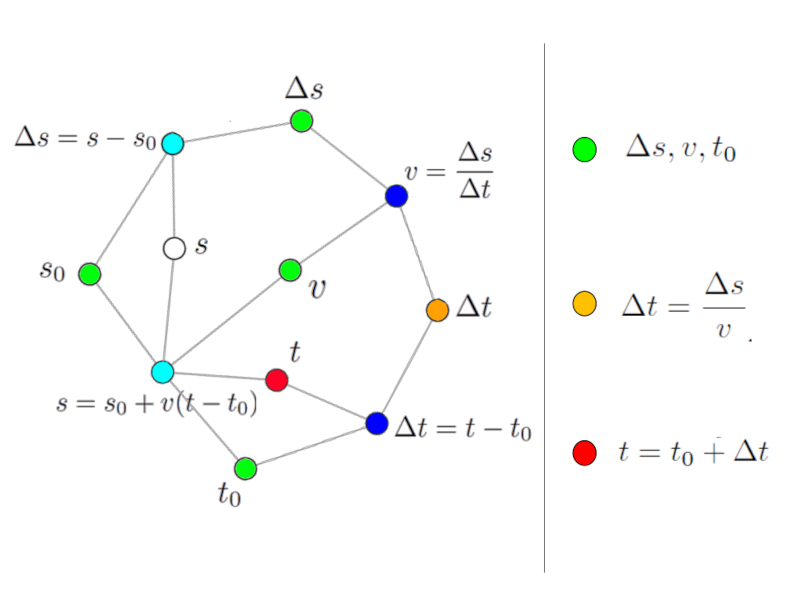
Solution via the intermediate variable travel time.

Every time we identify an equation that has only one unknown (white or red node) we can use that equation to calculate that value. To facilitate the interpretation we can give a color to the calculated variable (orange).

In this way we can generalize the rule:

A variable (white or red node) can only be calculated with an equation (light blue node) if all other variables are known (light green or orange nodes).

The variable calculated in addition to the search variable is called the intermediate variable.

ID:(14388, 0)