Resolver Problemas con Redes de Ecuaciones
Storyboard 
Los modelos se expresan en forma de redes de ecuaciones donde los distintos nodos son las variables del sistema.
Uno de los desafíos al resolver problemas en física es que solo se pueden emplear aquellas ecuaciones válidas para las condiciones existentes del problema en análisis. El modelo en sí se define en función de todas las ecuaciones que son válidas para la situación estudiada. Por lo tanto, el uso del modelo asegura que solo se empleen ecuaciones que correspondan a la situación a estudiar.
Al formar las diferentes ecuaciones del modelo mediante sus variables, una red se facilita para determinar la estrategia de resolución de un problema. La red misma permite identificar de manera directa las variables intermedias que se pueden calcular, definiendo así las variables necesarias y el orden en el que se deben calcular las variables intermedias hasta llegar a las variables buscadas.
En última instancia, los riesgos de cometer errores en el cálculo se reducen al seleccionar el modelo adecuado y asociar los parámetros dados con las variables del modelo.
ID:(1932, 0)
Ecuación: el camino recorrido
Imagen 
La ecuación del camino recorrido
$\Delta s = s - s_0$
se puede representar como un nodo (celeste) asociado a los nodos de la variable del camino recorrido $\Delta s$, la posición inicial $s_0$ y la posición final:
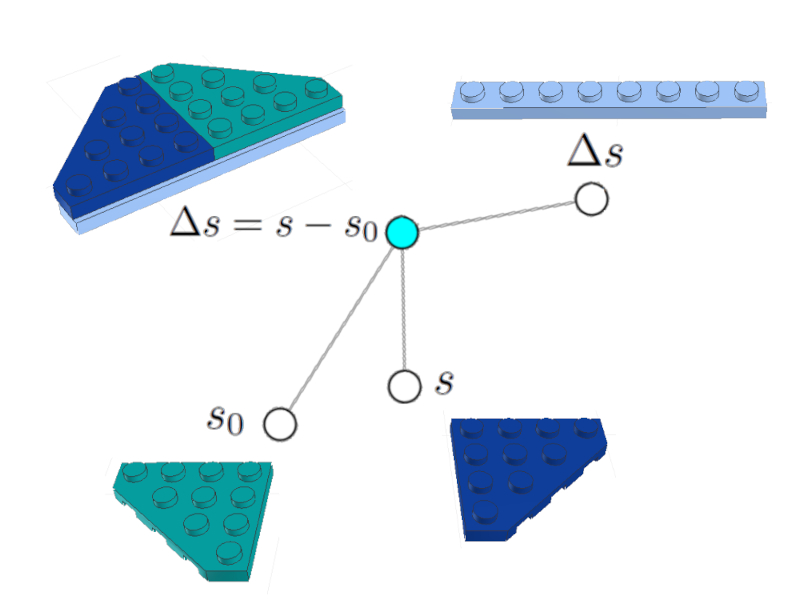
Ecuación del camino recorrido
Se incluyen las imágenes de los ladrillos de LEGO incluyendo la representación de la ecuación.
ID:(14379, 0)
Ecuación: el tiempo transcurrido
Imagen 
La ecuación del tiempo transcurrido
$\Delta t = t - t_0$
se puede representar como un nodo (celeste) asociado a los nodos de la variable del tiempo transcurrido $\Delta t$, el tiempo inicial $t_0$ y el tiempo final:
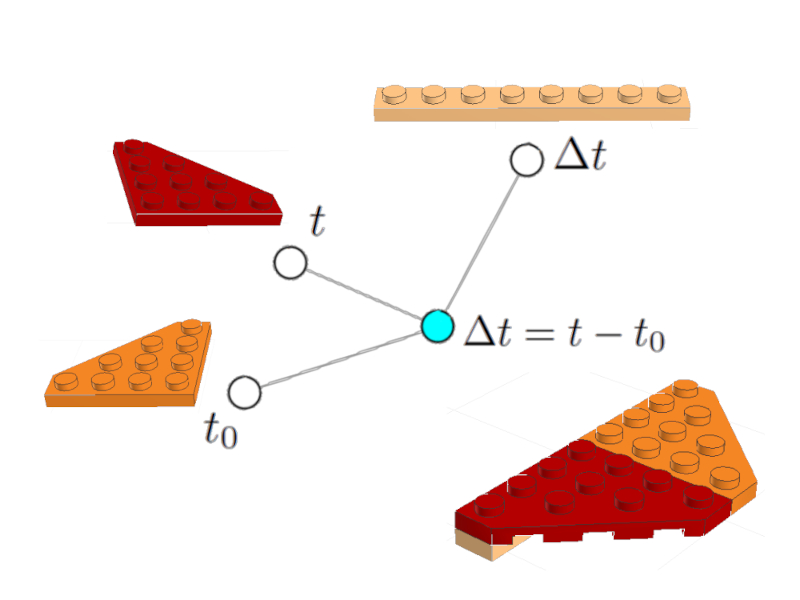
Ecuación del tiempo transcurrido
Se incluyen las imágenes de los ladrillos de LEGO incluyendo la representación de la ecuación.
ID:(14380, 0)
Ecuación: la velocidad
Imagen 
La ecuación de la velocidad
$v = \displaystyle\frac{\Delta s}{\Delta t}$
se puede representar como un nodo (celeste) asociado a los nodos de la variable de la velocidad $v$, el camino recorrido $\Delta s$ y el tiempo transcurrido $\Delta t$:
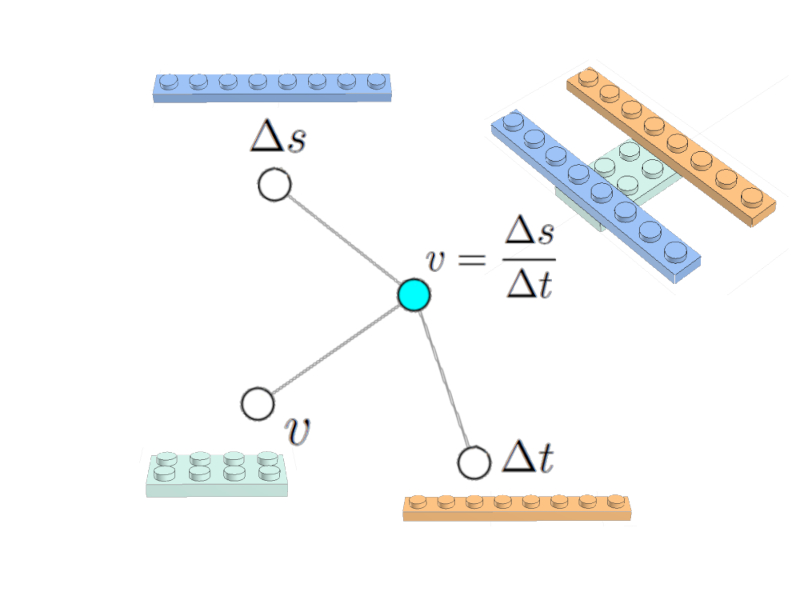
Ecuación de la velocidad
Se incluyen las imágenes de los ladrillos de LEGO incluyendo la representación de la ecuación.
ID:(14381, 0)
Ecuación: de la posición
Imagen 
Con las tres ecuaciones ya introducidas, se puede establecer una cuarta ecuación que permite calcular la posición en todo momento
$s = s_0 + v (t - t_0)$
que también se puede representar como un nodo (celeste) asociado a los nodos de la variable posición $s$, posición inicial $s_0$, velocidad $v$, tiempo inicial $t_0$ y el tiempo final $t$:
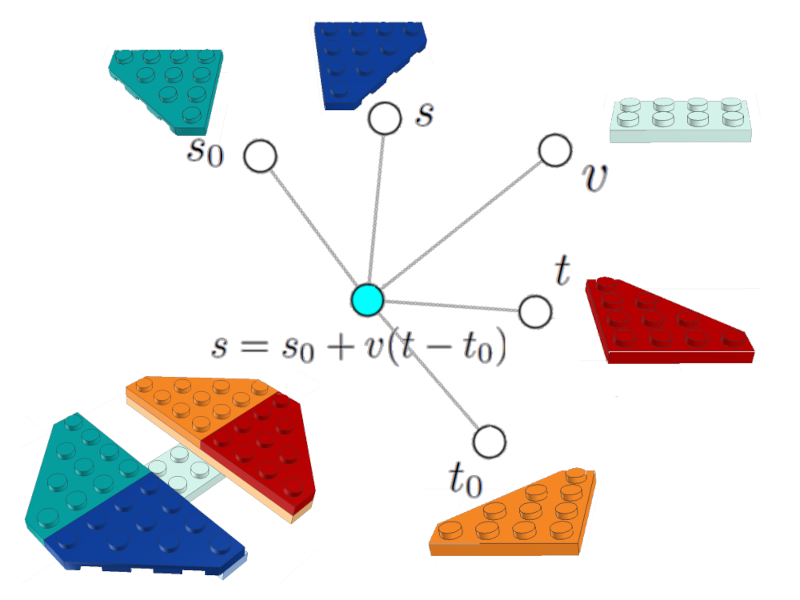
Ecuación de la posición
Se incluyen las imágenes de los ladrillos de LEGO incluyendo la representación de la ecuación.
ID:(14382, 0)
Formar la red
Imagen 
Si se dibujan todas las ecuaciones con sus respectivos grafos, se ve que existen variables en común que pueden ser integradas.
Es importante que cada variable aparezca solo una vez representada por su nodo (blanco)
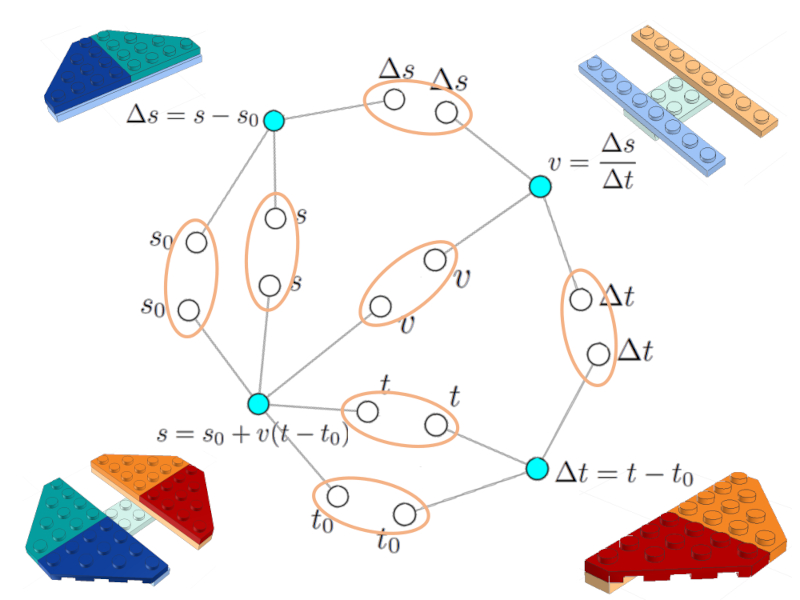
Formando la red
ID:(14383, 0)
La red
Imagen 
Una vez integradas las variables comunes, se obtiene la red que representa al modelo.
En este caso el modelo es simple, solo consta de 4 ecuaciones (nodos celestes) ligadas entre ellas mediante 7 variables (nodos blancos)
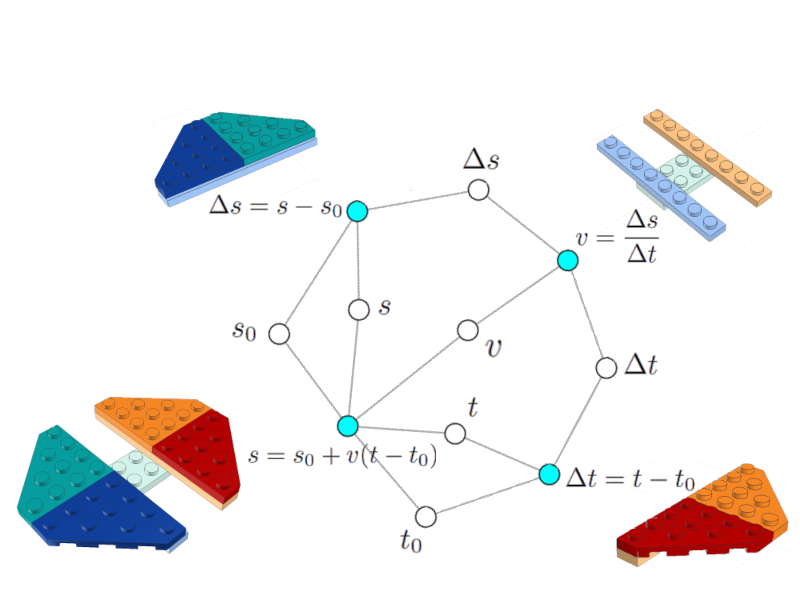
La red del modelo
Un modelo mas complejo puede tener múltiples ecuaciones y variables. Todas ellas ligadas formando una sola red.
ID:(14384, 0)
Variables a calcular
Imagen 
En principio toda variable del modelo puede ser calculada. En este caso en particular:
| $s$ | A que distancia vamos a llegar? |
| $s_0$ | A que distancia partimos? |
| $\Delta s$ | Que camino recorrimos? |
| $t$ | A que hora vamos a llegar? |
| $t_0$ | A que hora partimos? |
| $\Delta t$ | Que tiempo viajamos? |
| $v$ | A que velocidad viajamos? |
Si tomamos en caso de la hora en que vamos a arribar, podemos marcar con rojo el nodo correspondiente en la red del modelo:
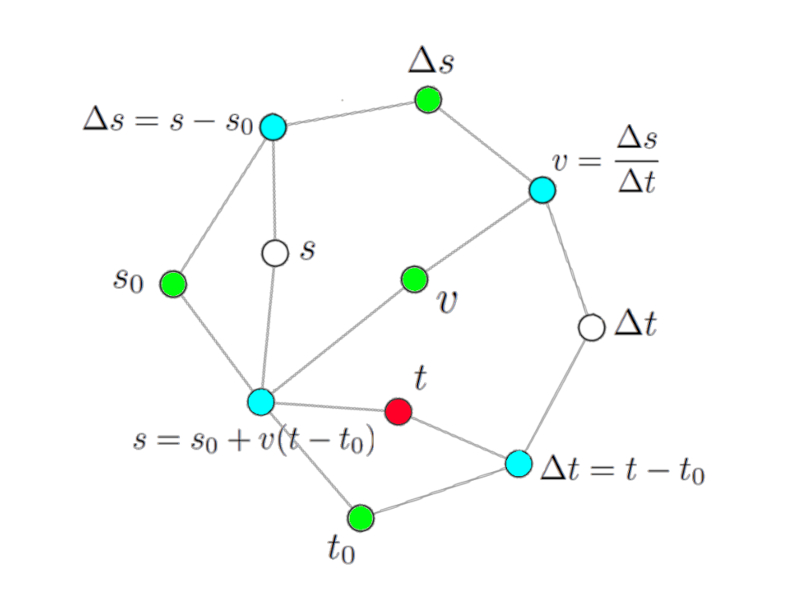
La red del modelo para el cálculo del tiempo de arribo.
Consultando la red observamos de inmediato los nodos asociados que corresponden a las ecuaciones que se pueden usar para calcular dicha variable. En este caso se marcaron en azul y corresponden a las ecuaciones
$s = s_0 + v (t - t_0)$
y
$\Delta t = t - t_0$
ID:(14385, 0)
Variables dadas
Imagen 
Para calcular una variable en particular se deben determinar primero las variables cuyos valores se nos dan.
Para facilitar la interpretación se pueden marcar los nodos de las variables dadas con otro color (verde claro).

La red del modelo con las variables dadas y la variable a calcular.
De esta forma es fácil ver que no se puede calcular la variable escogida pues ambas ecuaciones asociadas presentan variables para los que desconocemos sus valores (nodos blancos).
La regla en general es
Solo se puede calcular una variable (nodo blanco) si todos los restantes nodos asociados a una ecuación (nodo celeste) están dados (nodos verde claro). En general no pueden haber mas de un nodo blanco.
ID:(14386, 0)
Estrategia de solución via posición final
Imagen 
No se puede calcular la variable buscada (nodo rojo) porque en ambas ecuaciones asociadas existen otras variables desconocidas (nodos blancos).
Sin embargo es posible calcular estas mediante otras ecuaciones de la red. Para ello tomamos por ejemplo la variable $s$ que se puede calcular con la ecuación del camino recorrido:
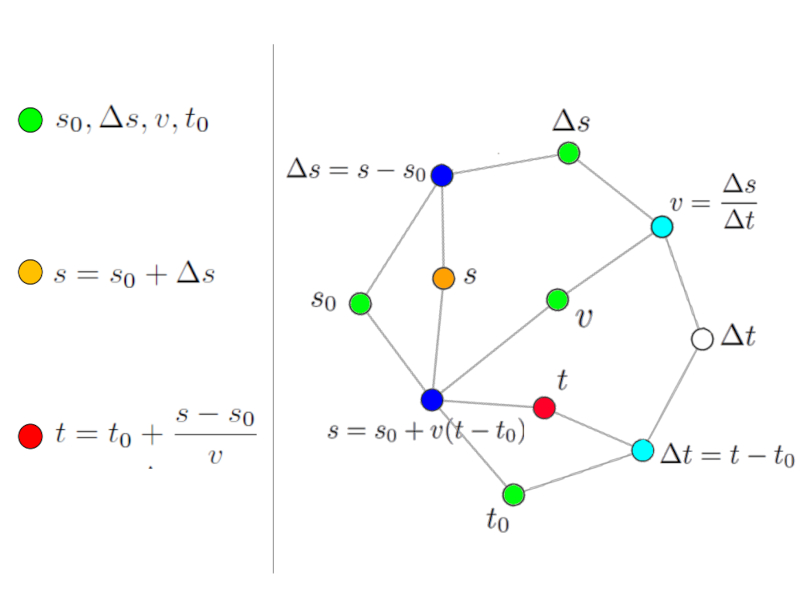
Solución via la variable intermedia posición final.
Cada vez que identificamos una ecuación que presenta solo una incógnita (nodo blanco o rojo) podemos usar dicha ecuación para calcular dicho valor. Para facilitar la interpretación podemos dar un color a la variable calculada (naranjo).
De esta forma podemos generalizar la regla:
Una variable (nodo blanco o rojo) solo puede ser calculada con una ecuación (nodo celeste) si todas las restantes variables son conocidas (nodos verde claros o naranjos).
La variable calculada adicionalmente a la variable buscada se denomina variable intermedia.
ID:(14387, 0)
Estrategia de solución via tiempo de viaje
Imagen 
No se puede calcular la variable buscada (nodo rojo) porque en ambas ecuaciones asociadas existen otras variables desconocidas (nodos blancos).
Sin embargo es posible calcular estas mediante otras ecuaciones de la red. Para ello tomamos por ejemplo la variable $\Delta t$ que se puede calcular con la ecuación del camino recorrido:
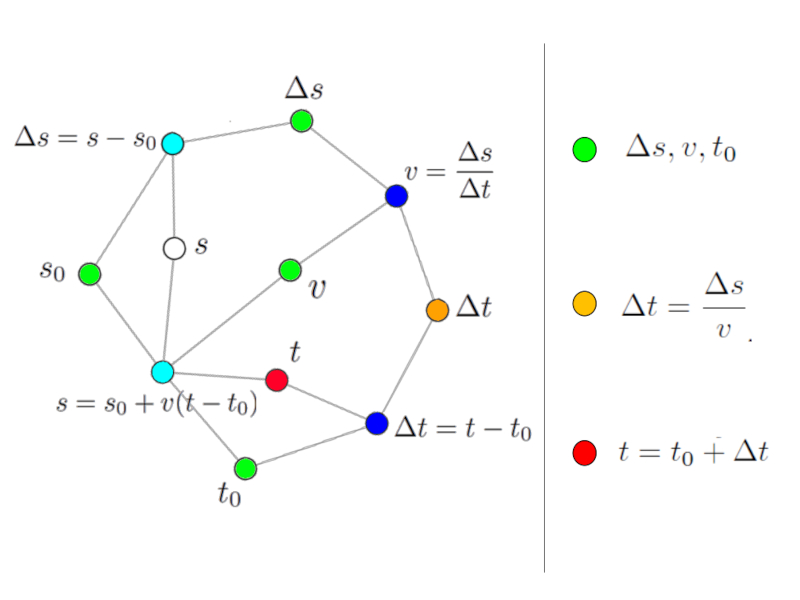
Solución via la variable intermedia tiempo de viaje.
Cada vez que identificamos una ecuación que presenta solo una incógnita (nodo blanco o rojo) podemos usar dicha ecuación para calcular dicho valor. Para facilitar la interpretación podemos dar un color a la variable calculada (naranjo).
De esta forma podemos generalizar la regla:
Una variable (nodo blanco o rojo) solo puede ser calculada con una ecuación (nodo celeste) si todas las restantes variables son conocidas (nodos verde claros o naranjos).
La variable calculada adicionalmente a la variable buscada se denomina variable intermedia.
ID:(14388, 0)
