Equação: o caminho percorrido
Imagem 
A equação do caminho percorrido
$\Delta s = s - s_0$
Pode ser representado como um nó (celeste) associado aos nós da variável de caminho percorrido $\Delta s$, a posição inicial $s_0$ e a posição final:
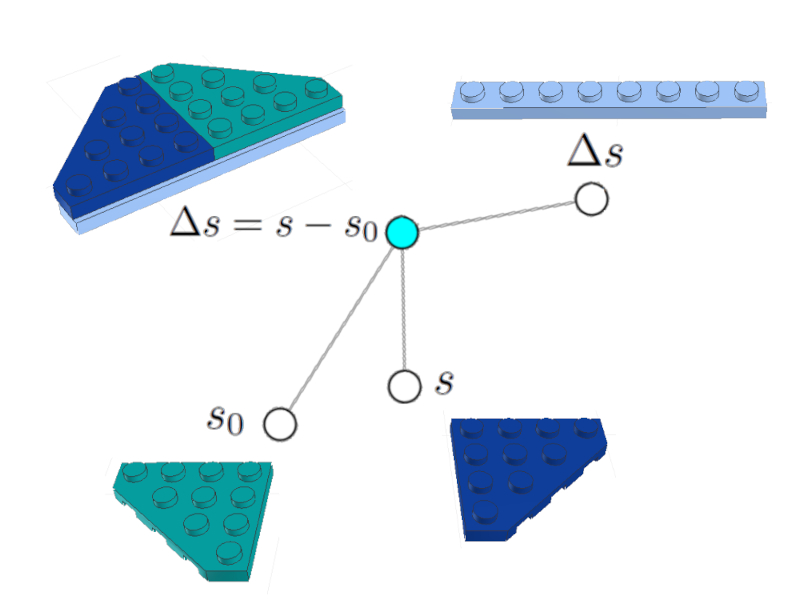
Equação do caminho percorrido
Estão incluídas imagens dos tijolos LEGO, incluindo a representação da equação.
ID:(14379, 0)
Equação: o tempo decorrido
Imagem 
A equação do tempo decorrido
$\Delta t = t - t_0$
Pode ser representado como um nó (celeste) associado aos nós da variável do tempo decorrido $\Delta t$, do tempo inicial $t_0$ e do tempo final:
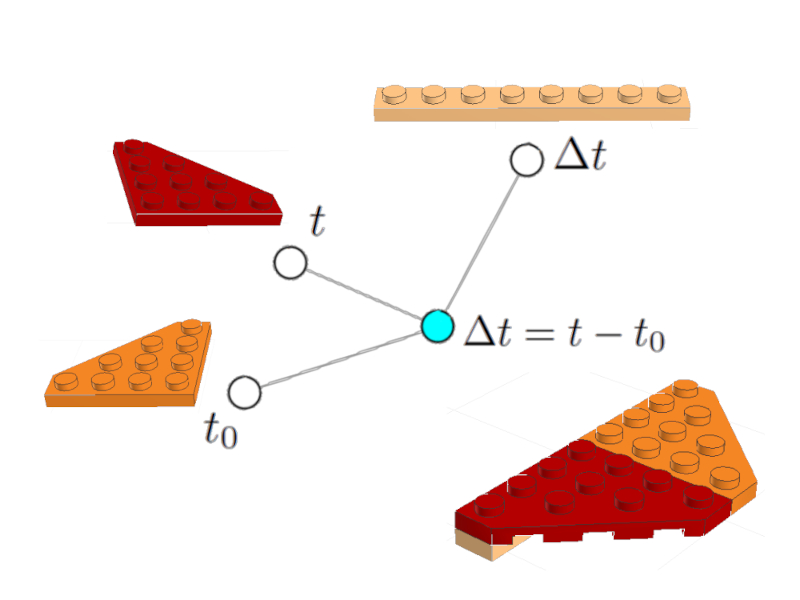
Equação do tempo decorrido
Estão incluídas imagens dos tijolos LEGO, incluindo a representação da equação.
ID:(14380, 0)
Equação: a velocidade
Imagem 
A equação da velocidade
$v = \displaystyle\frac{\Delta s}{\Delta t}$
Pode ser representado como um nó (celestial) associado aos nós da variável velocidade $v$, o caminho percorrido $\Delta s$ e o tempo decorrido $\Delta t$:
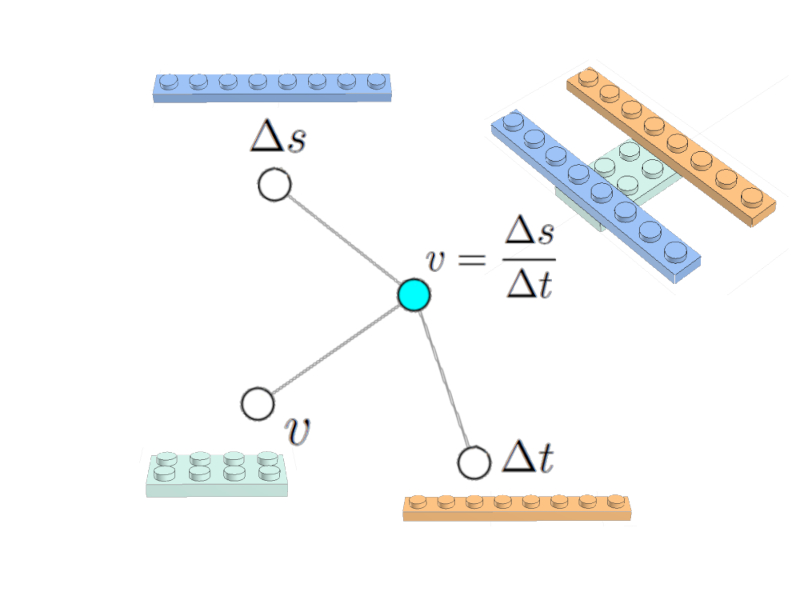
Equação da velocidade
Estão incluídas imagens dos tijolos LEGO, incluindo a representação da equação.
ID:(14381, 0)
Equação: de posição
Imagem 
Com as três equações já inseridas, pode-se estabelecer uma quarta equação que permite calcular a posição em todos os momentos
$s = s_0 + v(t - t_0)$
que também pode ser representado como um nó (celeste) associado aos nós da variável posição $s$, posição inicial $s_0$, velocidade $v$, tempo inicial $t_0$ e tempo final $t$:
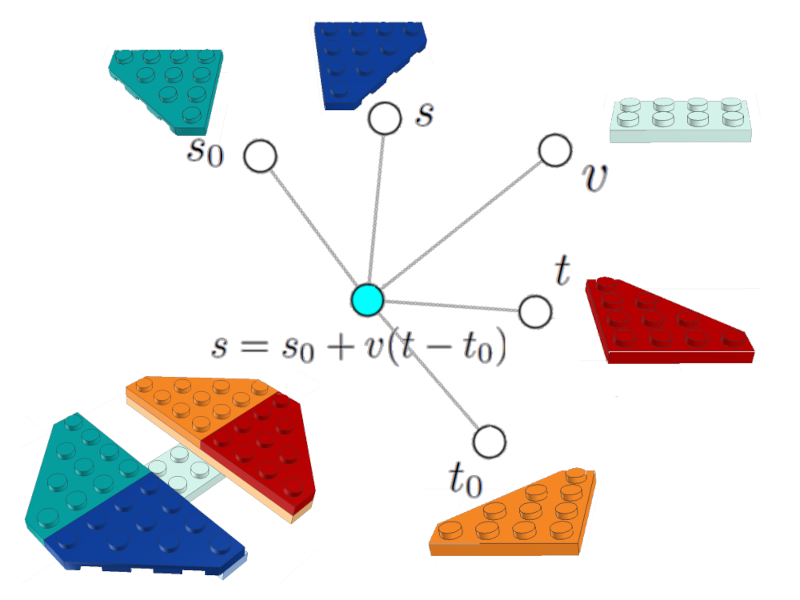
Equação de posição
Estão incluídas imagens dos tijolos LEGO, incluindo a representação da equação.
ID:(14382, 0)
Formar a rede
Imagem 
Se todas as equações forem desenhadas com seus respectivos gráficos, vê-se que existem variáveis comuns que podem ser integradas.
É importante que cada variável apareça apenas uma vez representada por seu nó (em branco)
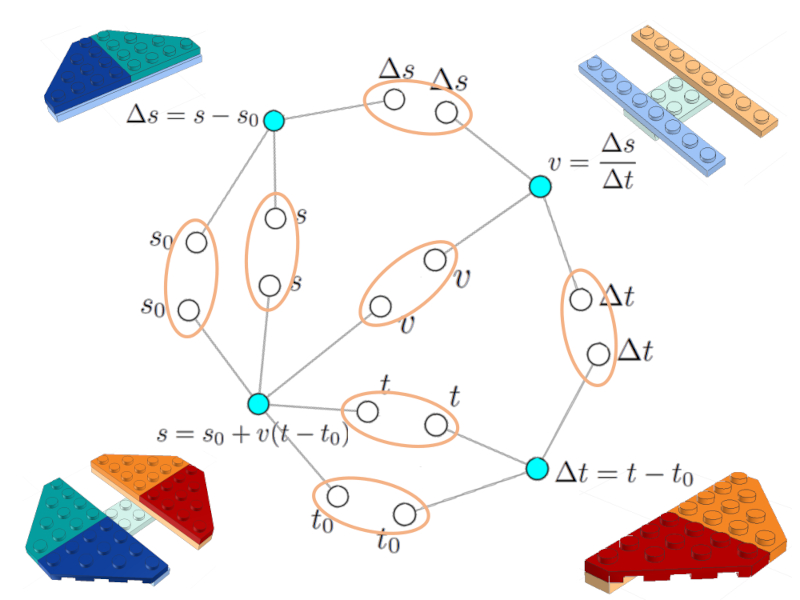
Formando a rede
ID:(14383, 0)
A rede
Imagem 
Uma vez integradas as variáveis comuns, obtém-se a rede que representa o modelo.
Neste caso, o modelo é simples, consiste apenas em 4 equações (nós celestes) ligadas entre si por 7 variáveis (nós brancos).
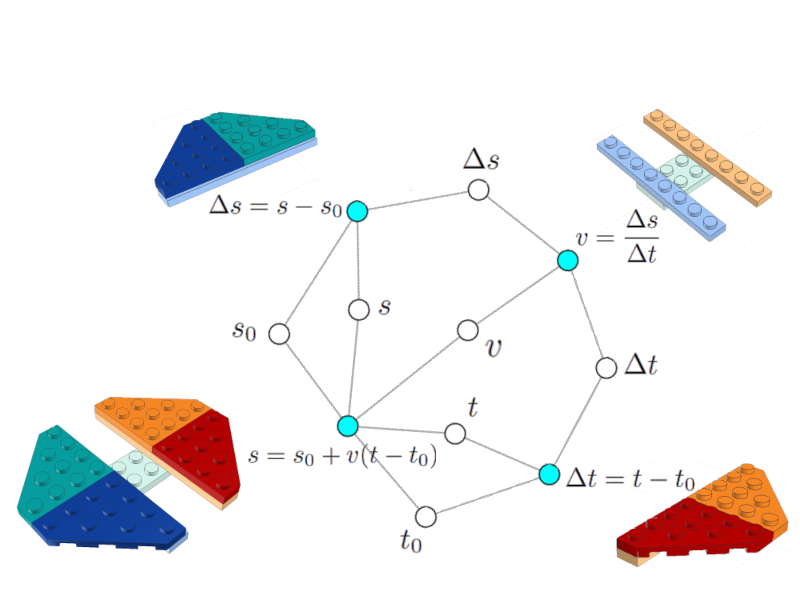
A rede modelo
Um modelo mais complexo pode ter várias equações e variáveis. Todos eles interligados formando uma única rede.
ID:(14384, 0)
Variáveis para calcular
Imagem 
Em princípio, todas as variáveis do modelo podem ser calculadas. Neste caso específico:
$s$: Até onde vamos?
$s_0$: A que distância começamos?
$\Delta s$: Para onde fomos?
$t$: Que horas vamos chegar?
$t_0$: A que horas saímos?
$\Delta t$: Quanto tempo viajamos?
$v$: Quão rápido estamos viajando?
Se levarmos em consideração o tempo que vamos chegar, podemos marcar o nó correspondente na rede modelo com vermelho:
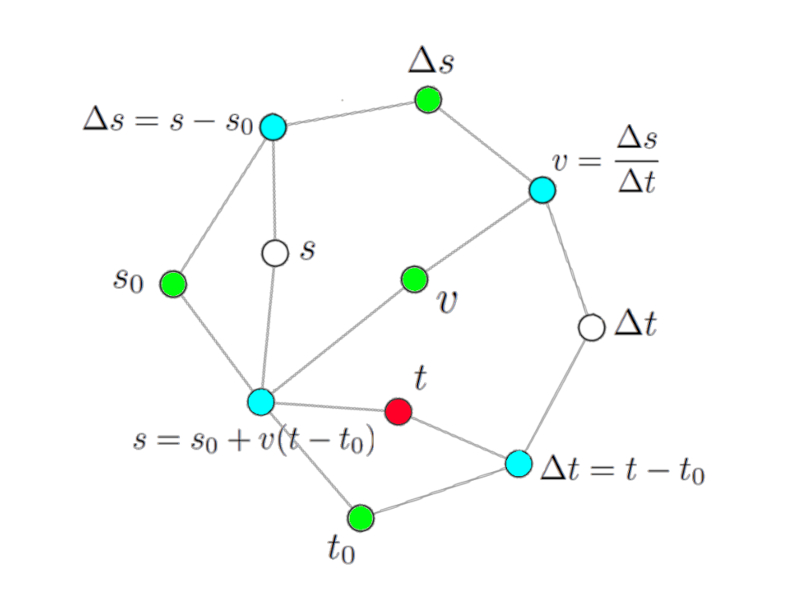
A rede modelo para calcular a hora de chegada.
Consultando a rede observamos imediatamente os nós associados que correspondem às equações que podem ser usadas para calcular a referida variável. Neste caso, eles foram marcados em azul e correspondem às equações
$s = s_0 + v(t - t_0)$
e
$\Delta t = t - t_0$
ID:(14385, 0)
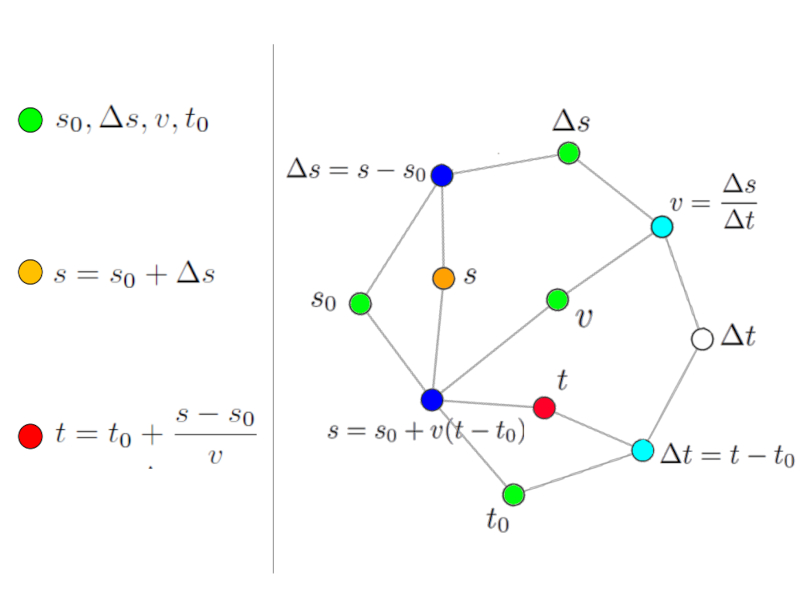
Variáveis dadas
Imagem 
Para calcular uma determinada variável, devemos primeiro determinar as variáveis cujos valores nos são dados.
Para facilitar a interpretação, os nós das variáveis dadas podem ser marcados com outra cor (verde claro).

A rede do modelo com as variáveis dadas e a variável a calcular.
Desta forma é fácil perceber que a variável escolhida não pode ser calculada visto que ambas as equações associadas apresentam variáveis para as quais não conhecemos os seus valores (nós brancos).
A regra geral é
ID:(14386, 0)
Estratégia de solução via posição final
Imagem 
A variável procurada (nó vermelho) não pode ser calculada porque em ambas as equações associadas existem outras variáveis desconhecidas (nós brancos).
No entanto, é possível calculá-los usando outras equações de rede. Para isso tomamos, por exemplo, a variável $s$ que pode ser calculada com a equação do caminho percorrido:
Solução através da posição final da variável intermediária.
Sempre que identificamos uma equação que possui apenas uma incógnita (nó branco ou vermelho), podemos usar essa equação para calcular esse valor. Para facilitar a interpretação podemos dar uma cor à variável calculada (laranja).
Assim podemos generalizar a regra:
Uma variável (nó branco ou vermelho) só pode ser calculada com uma equação (nó azul claro) se todas as outras variáveis forem conhecidas (nós verde claro ou laranja).
A variável calculada além da variável de pesquisa é chamada de variável intermediária.
ID:(14387, 0)
Estratégia de solução via tempo de viagem
Imagem 
A variável procurada (nó vermelho) não pode ser calculada porque em ambas as equações associadas existem outras variáveis desconhecidas (nós brancos).
No entanto, é possível calculá-los usando outras equações de rede. Para isso tomamos, por exemplo, a variável $\Delta t$ que pode ser calculada com a equação do caminho percorrido:
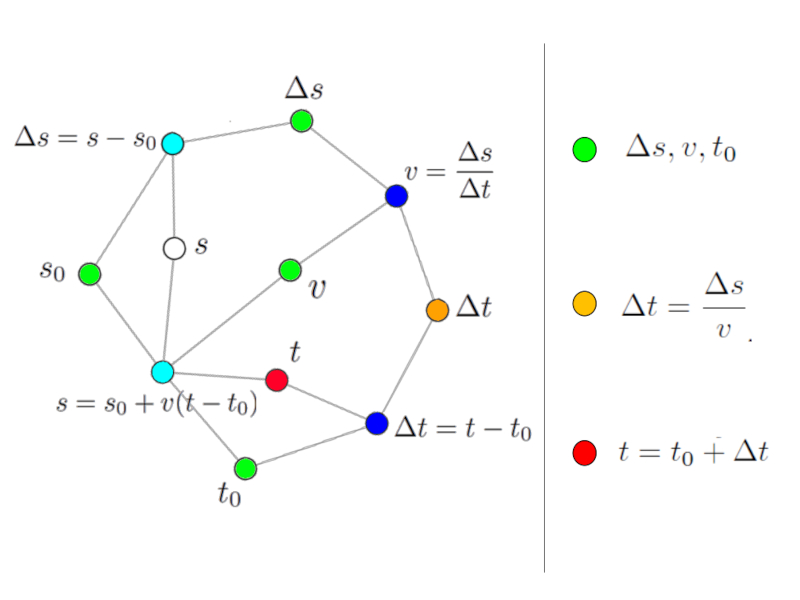
Solução via tempo de viagem variável intermediária.
Sempre que identificamos uma equação que possui apenas uma incógnita (nó branco ou vermelho), podemos usar essa equação para calcular esse valor. Para facilitar a interpretação podemos dar uma cor à variável calculada (laranja).
Assim podemos generalizar a regra:
Uma variável (nó branco ou vermelho) só pode ser calculada com uma equação (nó azul claro) se todas as outras variáveis forem conhecidas (nós verde claro ou laranja).
A variável calculada além da variável de pesquisa é chamada de variável intermediária.
ID:(14388, 0)
