Résoudre des Problèmes avec des réseaux d'équations
Storyboard 
Les modèles sont exprimés sous forme de réseaux d'équations où les différents nuds représentent les variables du système.
Un des défis lors de la résolution de problèmes en physique est que seules les équations valides pour les conditions existantes du problème en analyse peuvent être utilisées. Le modèle lui-même est défini sur la base de toutes les équations valides pour la situation étudiée. Ainsi, l'utilisation du modèle garantit que seules les équations correspondant à la situation étudiée soient utilisées.
En formant les différentes équations du modèle à l'aide de ses variables, un réseau est établi pour déterminer la stratégie de résolution du problème. Ce réseau permet l'identification directe des variables intermédiaires pouvant être calculées, définissant ainsi les variables nécessaires et l'ordre dans lequel les variables intermédiaires doivent être calculées jusqu'à ce que les variables souhaitées soient obtenues.
En fin de compte, les risques d'erreurs de calcul sont réduits par la sélection du modèle approprié et par l'association des paramètres donnés aux variables du modèle.
ID:(1932, 0)
Équation : le chemin parcouru
Image 
L'équation du chemin parcouru
$\Delta s = s - s_0$
Il peut être représenté comme un nud (céleste) associé aux nuds de la variable du chemin parcouru $\Delta s$, la position initiale $s_0$ et la position finale :
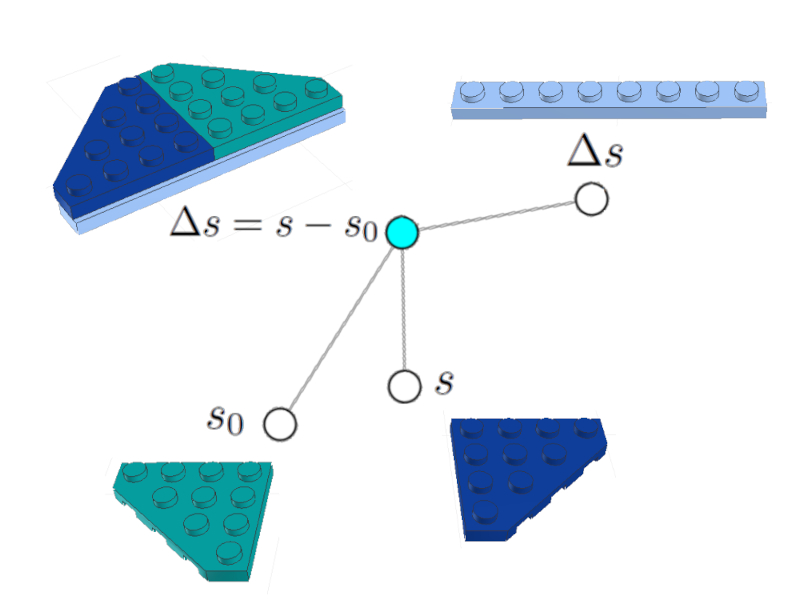
Équation du chemin parcouru
Des images des briques LEGO, y compris la représentation de l'équation, sont incluses.
ID:(14379, 0)
Équation : le temps écoulé
Image 
L'équation du temps écoulé
$\Delta t = t - t_0$
Il peut être représenté comme un nud (céleste) associé aux nuds de la variable du temps écoulé $\Delta t$, du temps initial $t_0$ et du temps final:
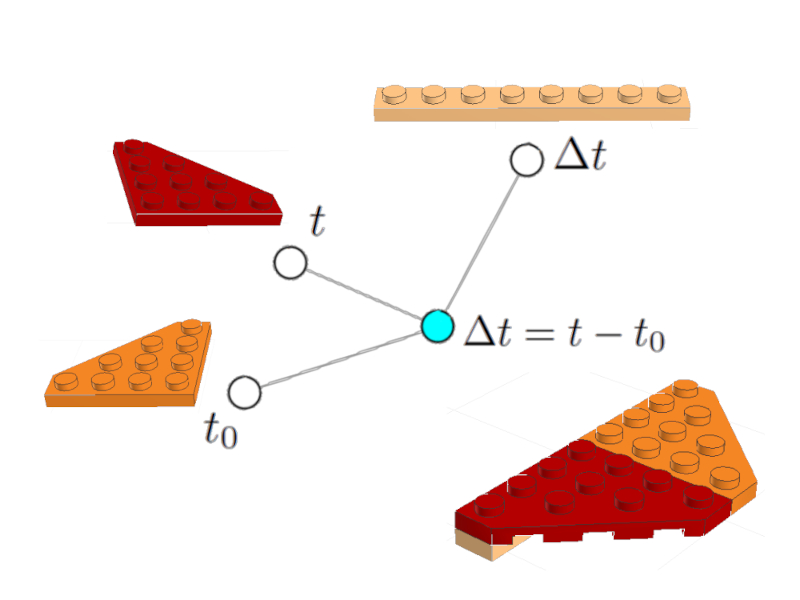
Équation du temps écoulé
Des images des briques LEGO, y compris la représentation de l'équation, sont incluses.
ID:(14380, 0)
Équation : la vitesse
Image 
L'équation de la vitesse
$v = \displaystyle\frac{\Delta s}{\Delta t}$
Il peut être représenté comme un nud (céleste) associé aux nuds de la variable de vitesse $v$, du chemin parcouru $\Delta s$ et du temps écoulé $\Delta t$ :
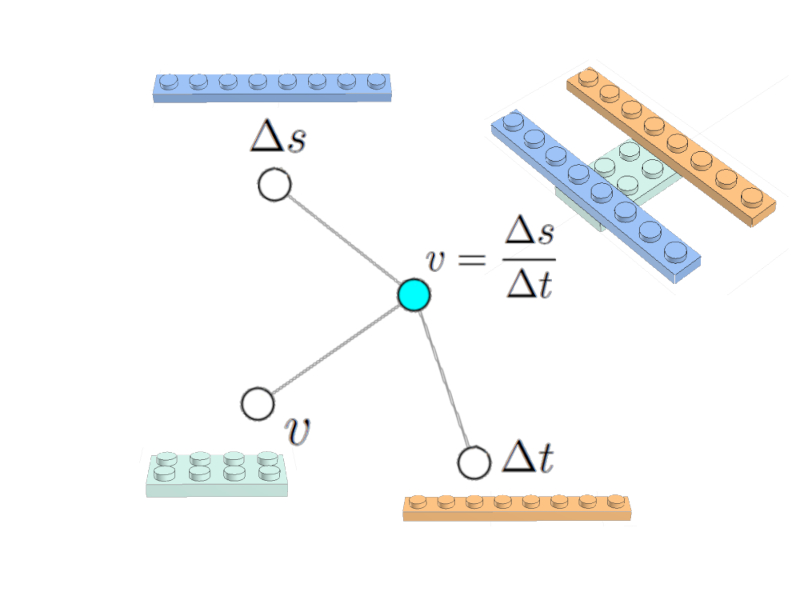
Équation de vitesse
Des images des briques LEGO, y compris la représentation de l'équation, sont incluses.
ID:(14381, 0)
Équation : de position
Image 
Avec les trois équations déjà entrées, une quatrième équation peut être établie qui permet de calculer la position à tout moment
$s = s_0 + v(t - t_0)$
qui peut aussi être représenté comme un nud (céleste) associé aux nuds de position variable $s$, position initiale $s_0$, vitesse $v$, temps initial $t_0$ et temps final $t$ :
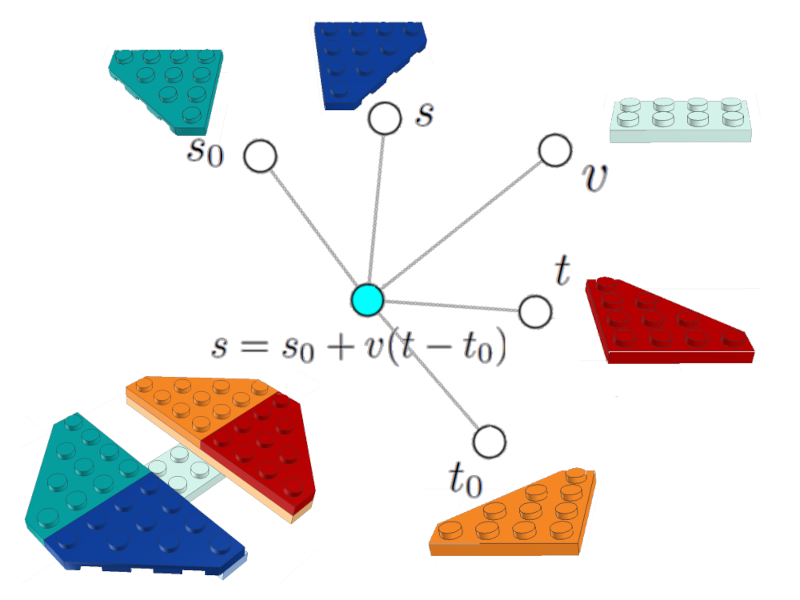
Équation de position
Des images des briques LEGO, y compris la représentation de l'équation, sont incluses.
ID:(14382, 0)
Forment le réseau
Image 
Si toutes les équations sont dessinées avec leurs graphiques respectifs, on voit qu'il existe des variables communes qui peuvent être intégrées.
Il est important que chaque variable n\'apparaisse qu\'une seule fois représentée par son nud (vide)
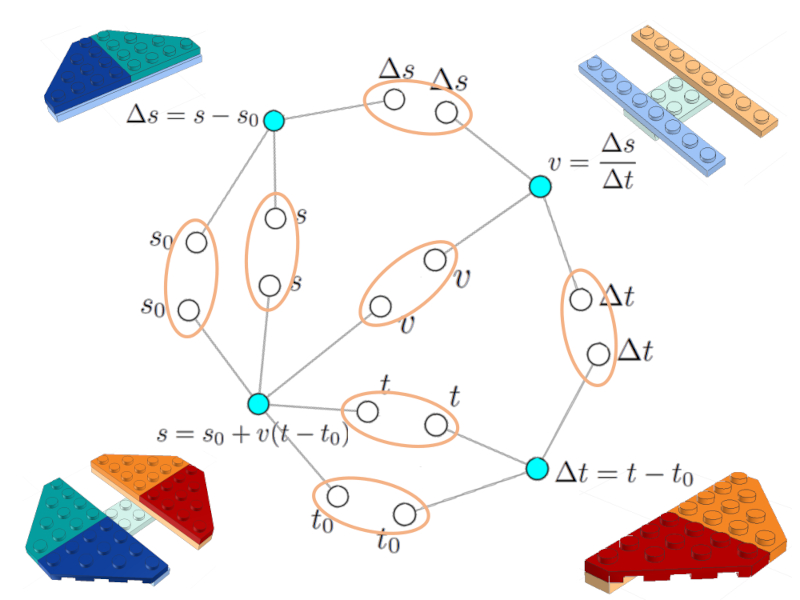
Formant le réseau
ID:(14383, 0)
Le réseau
Image 
Une fois les variables communes intégrées, le réseau qui représente le modèle est obtenu.
Dans ce cas, le modèle est simple, il se compose uniquement de 4 équations (nuds célestes) liées entre elles par 7 variables (nuds blancs).
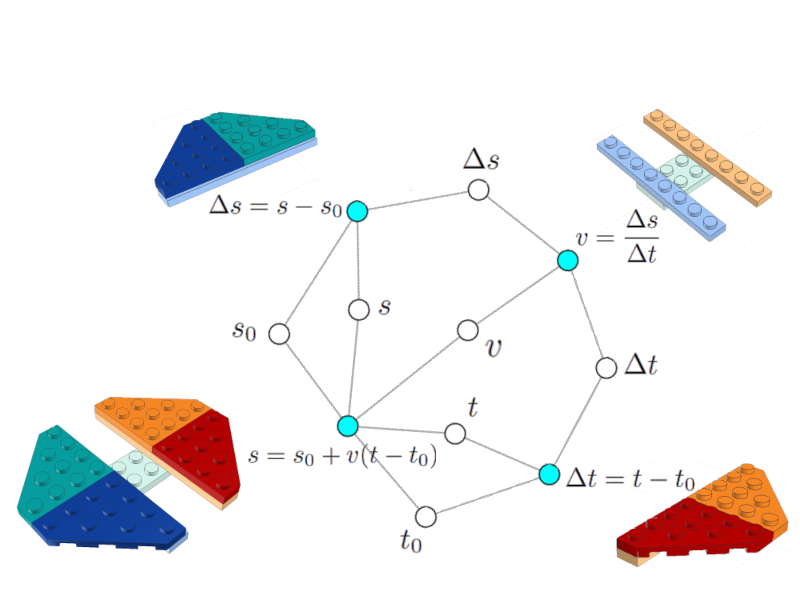
Le réseau modèle
Un modèle plus complexe peut avoir plusieurs équations et variables. Tous liés formant un seul réseau.
ID:(14384, 0)
Variables à calculer
Image 
En principe, chaque variable du modèle peut être calculée. Dans ce cas particulier :
| $s$ | Jusqu'où allons-nous aller ? |
| $s_0$ | À quelle distance commençons-nous ? |
| $\Delta s$ | Dans quelle direction sommes-nous allés ? |
| $t$ | À quelle heure allons-nous arriver ? |
| $t_0$ | À quelle heure partons-nous ? |
| $\Delta t$ | Combien de temps avons-nous voyagé ? |
| $v$vÀ quelle vitesse voyageons-nous ? |
Si nous prenons en compte l'heure à laquelle nous allons arriver, nous pouvons marquer en rouge le nud correspondant dans le réseau modèle :
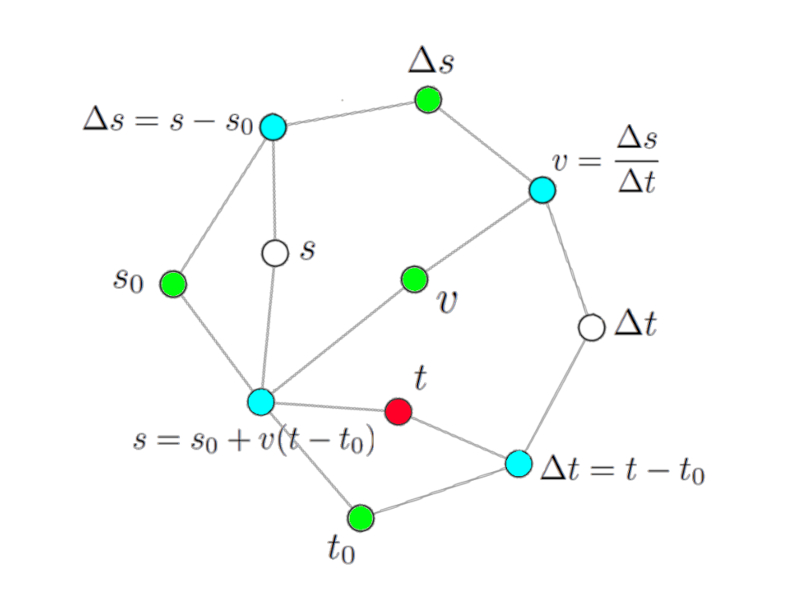
Le réseau modèle pour le calcul de l'heure d'arrivée.
En consultant le réseau, nous observons immédiatement les nuds associés qui correspondent aux équations pouvant être utilisées pour calculer ladite variable. Dans ce cas, ils ont été marqués en bleu et correspondent aux équations
$s = s_0 + v(t - t_0)$
et
$\Delta t = t - t_0$
ID:(14385, 0)
Variables données
Image 
Pour calculer une variable particulière, il faut d'abord déterminer les variables dont on nous donne les valeurs.
Pour faciliter l'interprétation, les nuds des variables données peuvent être marqués d\'une autre couleur (vert clair).

Le réseau du modèle avec les variables données et la variable à calculer.
De cette façon, il est facile de voir que la variable choisie ne peut pas être calculée puisque les deux équations associées présentent des variables pour lesquelles on ne connaît pas leurs valeurs (nuds blancs).
La règle générale est
ID:(14386, 0)
Stratégie de solution via la position finale
Image 
La variable recherchée (nud rouge) ne peut pas être calculée car dans les deux équations associées il y a d'autres variables inconnues (nuds blancs).
Cependant, il est possible de les calculer en utilisant d\'autres équations de réseau. Pour cela on prend par exemple la variable $s$ que l\'on peut calculer avec l\'équation du chemin parcouru :
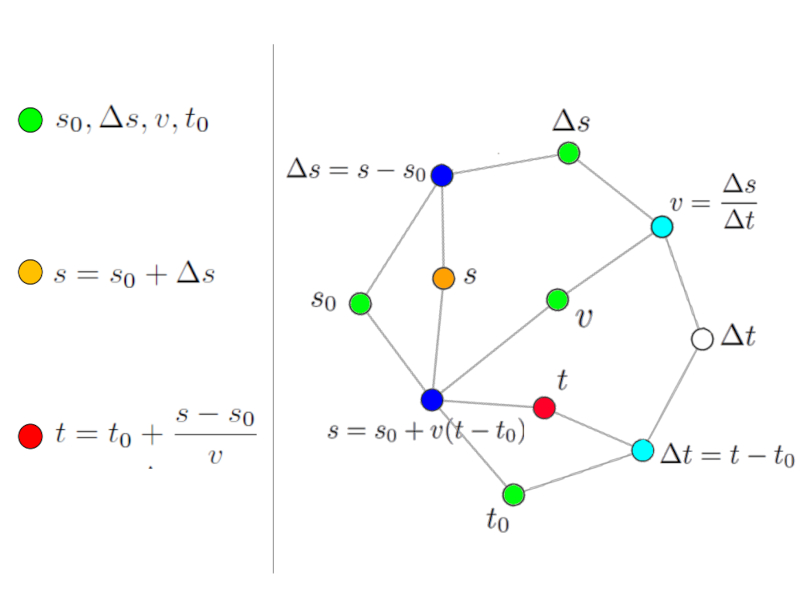
Solution via la variable intermédiaire position finale.
Chaque fois que nous identifions une équation qui n\'a qu\'une seule inconnue (nud blanc ou rouge), nous pouvons utiliser cette équation pour calculer cette valeur. Pour faciliter l\'interprétation on peut donner une couleur à la variable calculée (orange).
On peut ainsi généraliser la règle :
Une variable (nud blanc ou rouge) ne peut être calculée avec une équation (nud bleu clair) que si toutes les autres variables sont connues (nuds vert clair ou orange).
La variable calculée en plus de la variable de recherche est appelée variable intermédiaire.
ID:(14387, 0)
Stratégie de solution via le temps de déplacement
Image 
La variable recherchée (nud rouge) ne peut pas être calculée car dans les deux équations associées il y a d'autres variables inconnues (nuds blancs).
Cependant, il est possible de les calculer en utilisant d\'autres équations de réseau. Pour cela on prend par exemple la variable $\Delta t$ que l\'on peut calculer avec l\'équation du chemin parcouru :
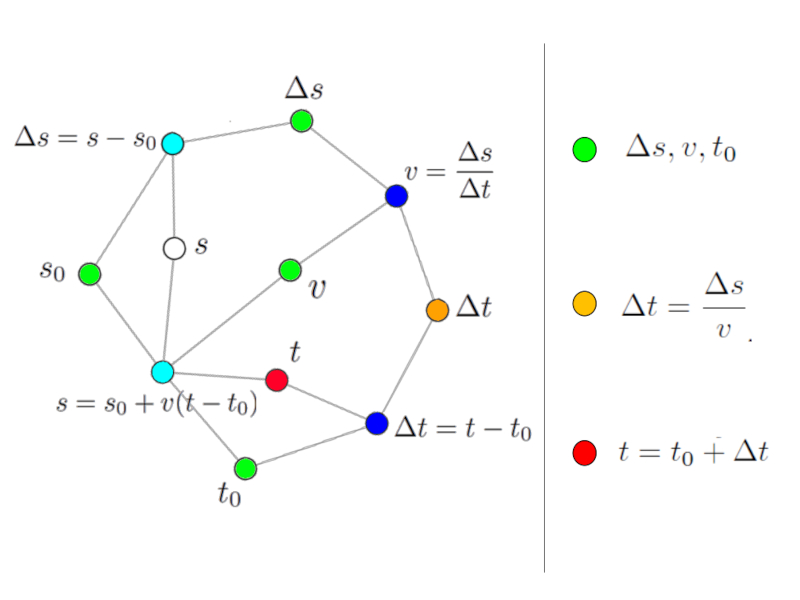
Solution via le temps de parcours variable intermédiaire.
Chaque fois que nous identifions une équation qui n\'a qu\'une seule inconnue (nud blanc ou rouge), nous pouvons utiliser cette équation pour calculer cette valeur. Pour faciliter l\'interprétation on peut donner une couleur à la variable calculée (orange).
On peut ainsi généraliser la règle :
Une variable (nud blanc ou rouge) ne peut être calculée avec une équation (nud bleu clair) que si toutes les autres variables sont connues (nuds vert clair ou orange).
La variable calculée en plus de la variable de recherche est appelée variable intermédiaire.
ID:(14388, 0)
