Druyd:Knowledge

El Ciclo de Stirling

Storyboard

Una máquina termodinámica que no emplea combustión interna, sino que únicamente recibe calor aplicado desde el exterior. A través de este proceso, se genera el ciclo típico en el espacio de presión-volumen y se puede modelar y calcular la eficiencia alcanzada.

>Modelo

ID:(1485, 0)

Mecanismos

Concepto

El ciclo de Stirling involucra cuatro fases principales: calentamiento, expansión, enfriamiento y compresión, realizadas en un ambiente sellado donde un gas como el helio o el hidrógeno actúa como fluido de trabajo.

Durante la fase de calentamiento, el gas se calienta a volumen constante, absorbiendo calor de una fuente externa lo que aumenta su temperatura y presión. Esto es seguido por la fase de expansión, donde el gas calentado se expande y realiza trabajo sobre un pistón u otro mecanismo, disminuyendo su temperatura y presión pero convirtiendo el calor en energía mecánica.

Luego ocurre la fase de enfriamiento a volumen constante. Aquí, el gas pierde calor, lo que disminuye su temperatura y presión, preparándolo para la fase final. El regenerador juega un papel crítico al absorber calor del gas, lo que conserva energía y mejora la eficiencia.

El ciclo concluye con la compresión del gas enfriado, lo cual requiere menos energía de la que se produjo durante la expansión. Esta compresión aumenta la temperatura del gas, aunque no tanto como durante la fase inicial de calentamiento, y el ciclo comienza de nuevo.

El regenerador es vital durante todo este proceso, almacenando calor de la fase de enfriamiento y devolviéndolo durante el calentamiento, reutilizando así la energía dentro del sistema y aumentando significativamente la eficiencia térmica del motor. Los motores Stirling son valorados por su operación silenciosa y la flexibilidad para usar cualquier fuente de calor, haciéndolos adaptables y beneficiosos para el medio ambiente en diversas aplicaciones.

ID:(15284, 0)

Ciclo de Carnot

Concepto

Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:

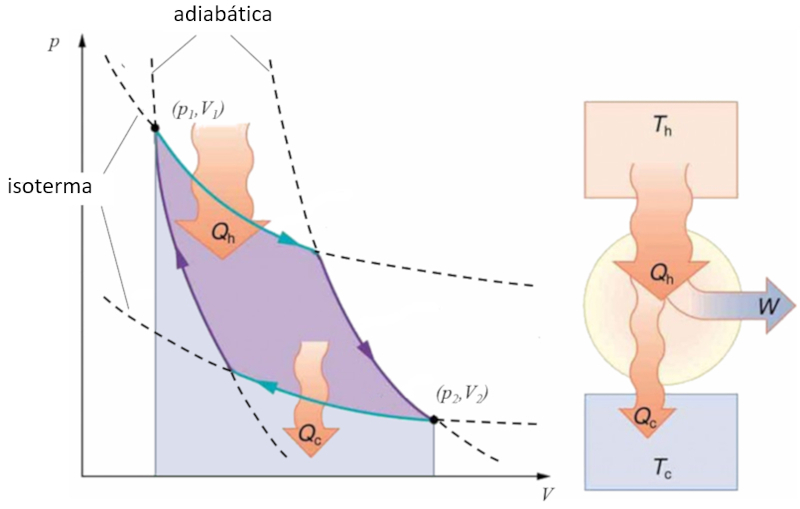
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.

Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work. [1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las máquinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)

ID:(11131, 0)

Ciclo de Stirling: Diagrama presión-volumen

Concepto

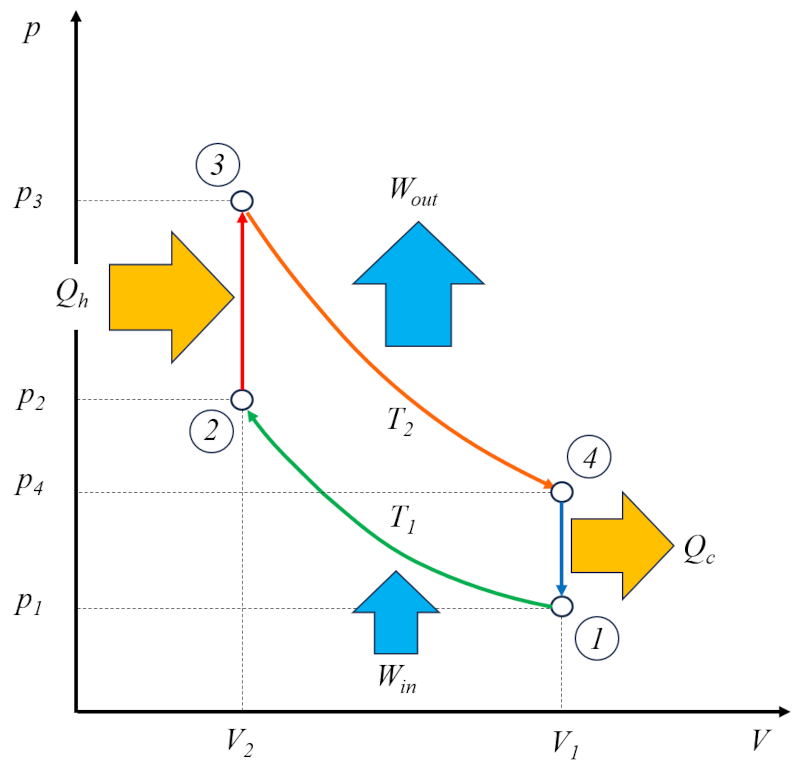
El ciclo de Stirling [1] puede considerarse como una solución técnica basada en el ciclo de Carnot, que consta de cuatro etapas bien definidas:

Etapa 1 a 2: Compresión isotérmica $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_1)$.
Etapa 2 a 3: Calentamiento isocórico $(p_2,V_2,T_1)\rightarrow(p_3,V_2,T_2)$.
Etapa 3 a 4: Expansión isotérmica $(p_3,V_2,T_2)\rightarrow(p_4,V_1,T_2)$.
Etapa 4 a 1: Enfriamiento isocórico $(p_4,V_1,T_2)\rightarrow(p_1,V_1,T_1)$.

Es importante destacar que este ciclo no involucra una etapa adiabática; en cambio, se basa en el intercambio entre procesos isocóricos (a volumen constante) y procesos isotérmicos (a temperatura constante).

Estas etapas se pueden visualizar en el siguiente diagrama:

[1] "An Economical Engine for the Purpose of Pumping Water by the Expansive Force of Steam" (Un motor económico para bombear agua mediante la fuerza expansiva del vapor), Robert Stirling, British Patent No. 4081 de 1816.

ID:(15362, 0)

Ciclo de Stirling 1 a 2

Concepto

En la primera etapa el número de moles ($n$) del gas es comprimido con el trabajo realizado sobre el sistema ($W_{in}$) desde el volumen expandido ($V_1$) a el volumen comprimido ($V_2$) en forma isotermica a la temperatura en estado 1 ($T_1$):

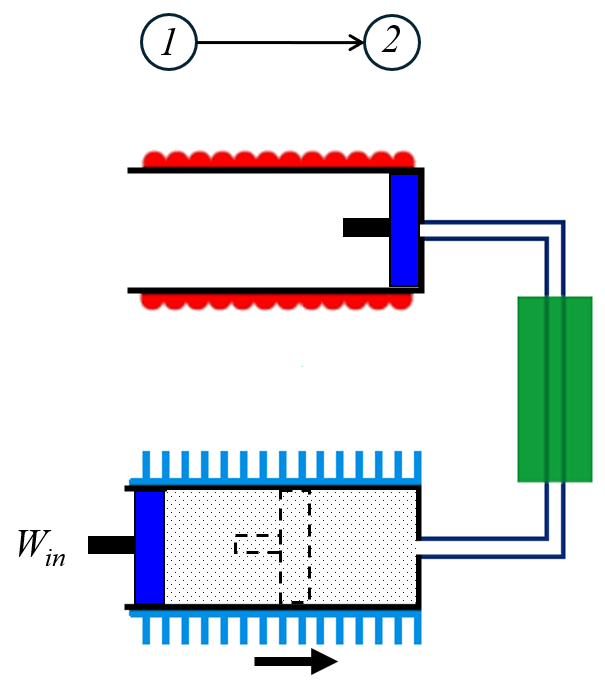
El trabajo se calcula utilizando la integral de el trabajo realizado sobre el sistema ($W_{in}$) con el número de moles ($n$) y la presión ($p$), integrada en el volumen ($V$), desde el volumen expandido ($V_1$) hasta el volumen comprimido ($V_2$):

$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$

Si la presión ($p$) se obtiene utilizando la constante universal de los gases ($R_C$), el número de moles ($n$) y la temperatura absoluta ($T$) con la ecuación de los gases

$ p V = n R_C T $

la integral para la temperatura absoluta ($T$) es igual a la temperatura en estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Por lo tanto,

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

ID:(15760, 0)

Ciclo de Stirling 2 a 3

Concepto

En la segunda etapa se agrega el calor suministrado ($Q_H$) que hace, dependiendo de la capacidad calórica a volumen constante ($C_V$), aumenta la temperatura de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$):

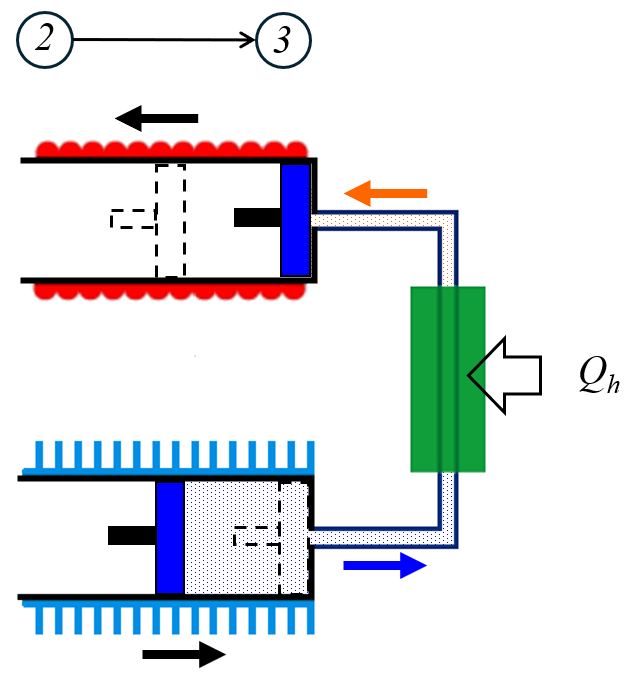
Al agregar el calor suministrado ($Q_H$) cuando el volumen ($V$) es igual al ERROR:8497,0 La temperatura absoluta ($T$) aumenta de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$). Esto implica que podemos utilizar la relación para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuación:

$ dU = C_V \Delta T $

esto nos lleva a la expresión:

$ Q_h = C_V ( T_2 - T_1 )$

ID:(15761, 0)

Ciclo de Stirling 3 a 4

Concepto

En la tercera etapa el número de moles ($n$) del gas expande realizando el trabajo realizado por el sistema ($W_{out}$) mientras el volumen se expande desde el volumen comprimido ($V_2$) a el volumen expandido ($V_1$) en forma isotermica a la temperatura en estado 2 ($T_2$):

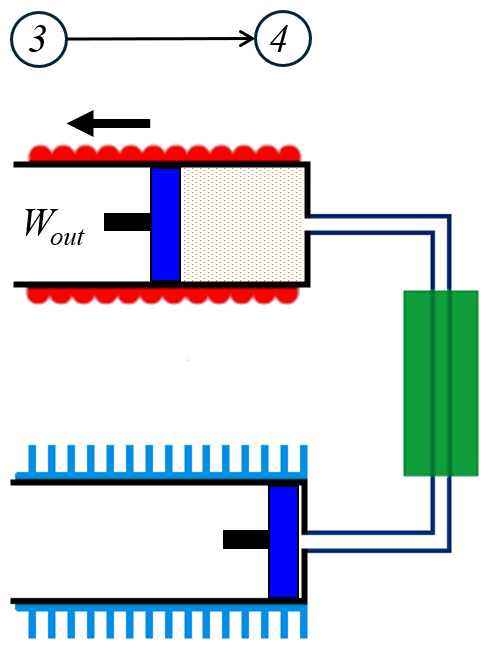
El cálculo del trabajo se realiza mediante la integral de el trabajo realizado por el sistema ($W_{out}$) con la presión ($p$), integrada en el volumen ($V$), desde el volumen expandido ($V_1$) hasta el volumen comprimido ($V_2$):

$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$

Si la presión ($p$) se obtiene mediante la constante universal de los gases ($R_C$), el número de moles ($n$), y la temperatura absoluta ($T$) usando la ecuación de los gases

$ p V = n R_C T $

se obtiene la integral para la temperatura absoluta ($T$) igual a la temperatura en estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Por lo tanto,

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

ID:(15762, 0)

Ciclo de Stirling 4 a 1

Concepto

En la cuarta etapa se reduce el calor absorbido ($Q_C$) que hace, dependiendo de la capacidad calórica a volumen constante ($C_V$), disminuir la temperatura de la temperatura en estado 2 ($T_2$) a la temperatura en estado 1 ($T_1$):

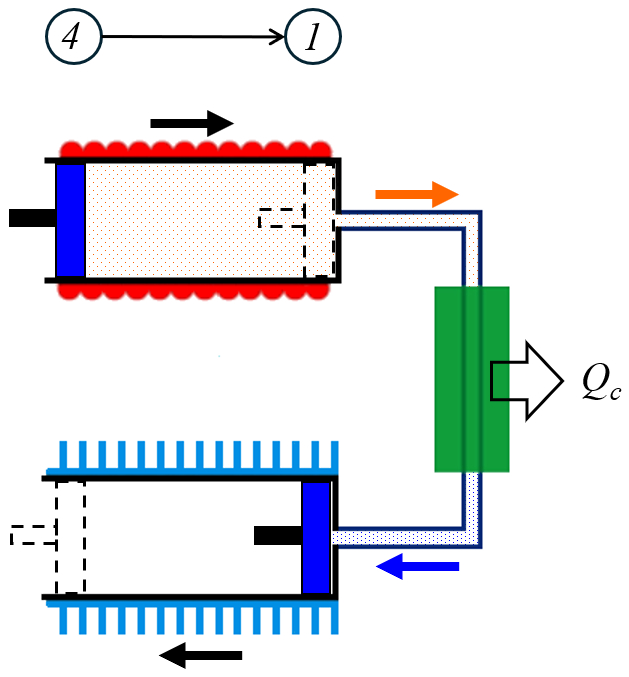
Al eliminar el calor absorbido ($Q_C$) cuando el volumen ($V$) es igual al ERROR:8498,0 La temperatura absoluta ($T$) aumenta de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$). Esto implica que podemos utilizar la relación para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuación:

$ dU = C_V \Delta T $

esto nos lleva a la expresión:

$ Q_c = C_V ( T_1 - T_2 )$

ID:(15763, 0)

Rendimiento de ciclo de Stirling

Concepto

La eficiencia ($\eta$) se define como la proporción entre el trabajo efectivo ($W$) y el calor aportado al sistema ($Q$):

$ \eta \equiv \displaystyle\frac{ W }{ Q } $

donde el trabajo efectivo ($W$) está relacionado con el trabajo realizado por el sistema ($W_{out}$) y el trabajo realizado sobre el sistema ($W_{in}$) mediante:

$ W \equiv W_{out} - W_{in} $

mientras que el calor aportado al sistema ($Q$) está asociado con el calor suministrado ($Q_H$), cuyo valor se establece en:

$ Q \equiv W_{in} + Q_h $

Dado que el trabajo realizado por el sistema ($W_{out}$) se relaciona con el número de moles ($n$), la temperatura en estado 2 ($T_2$), el volumen expandido ($V_1$), el volumen comprimido ($V_2$) y la constante universal de los gases ($R_C$) mediante:

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

y el trabajo realizado sobre el sistema ($W_{in}$) se asocia con la temperatura en estado 1 ($T_1$) por:

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

y el calor suministrado ($Q_H$) se relaciona con la capacidad calórica a volumen constante ($C_V$) en:

$ Q_h = C_V ( T_2 - T_1 )$

se puede calcular la eficiencia ($\eta$) resultando en:

$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R_C \ln( V_2 / V_1 )}}$

ID:(15764, 0)

Modelo

Concepto

ID:(15343, 0)

El Ciclo de Stirling

Modelo

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$Q_C$

Q_C

Calor absorbido

$Q$

Calor aportado al sistema

$Q_H$

Q_H

Calor suministrado

$C_V$

C_V

Capacidad calórica a volumen constante

J/kg

$R_C$

R_C

Constante universal de los gases

J/K mol

$\eta$

eta

Eficiencia

$n$

Número de moles

mol

$T_1$

T_1

Temperatura en estado 1

$T_2$

T_2

Temperatura en estado 2

$W$

Trabajo efectivo

$W_{out}$

W_out

Trabajo realizado por el sistema

$W_{in}$

W_in

Trabajo realizado sobre el sistema

$V_2$

V_2

Volumen comprimido

m^3

$V_1$

V_1

Volumen expandido

m^3

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ Q_h = C_V ( T_2 - T_1 )$

Q_H = C_V *( T_2 - T_1 )

Al agregar el calor suministrado ($Q_H$) cuando el volumen ($V$) es igual al ERROR:8497,0 La temperatura absoluta ($T$) aumenta de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:

$ dU = C_V \Delta T $

esto nos lleva a la expresi n:

$ Q_h = C_V ( T_2 - T_1 )$

(ID 15363)

$ Q_c = C_V ( T_1 - T_2 )$

Q_C = C_V *( T_1 - T_2 )

Al eliminar el calor absorbido ($Q_C$) cuando el volumen ($V$) es igual al ERROR:8498,0 La temperatura absoluta ($T$) aumenta de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:

$ dU = C_V \Delta T $

esto nos lleva a la expresi n:

$ Q_c = C_V ( T_1 - T_2 )$

(ID 15364)

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

W_in = n * R_C * T_1 * log( V_2 / V_1 )

$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$

Si la presión ($p$) se obtiene utilizando la constante universal de los gases ($R_C$), el número de moles ($n$) y la temperatura absoluta ($T$) con la ecuaci n de los gases

$ p V = n R_C T $

la integral para la temperatura absoluta ($T$) es igual a la temperatura en estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Por lo tanto,

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

(ID 15365)

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

W_out = n * R_C * T_2 * log( V_2 / V_1 )

El c lculo del trabajo se realiza mediante la integral de el trabajo realizado por el sistema ($W_{out}$) con la presión ($p$), integrada en el volumen ($V$), desde el volumen expandido ($V_1$) hasta el volumen comprimido ($V_2$):

$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$

Si la presión ($p$) se obtiene mediante la constante universal de los gases ($R_C$), el número de moles ($n$), y la temperatura absoluta ($T$) usando la ecuaci n de los gases

$ p V = n R_C T $

se obtiene la integral para la temperatura absoluta ($T$) igual a la temperatura en estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Por lo tanto,

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

(ID 15366)

$ \eta \equiv \displaystyle\frac{ W }{ Q } $

eta = W / Q

(ID 15756)

$ Q \equiv W_{in} + Q_h $

Q = W_in + Q_h

(ID 15757)

$ W \equiv W_{out} - W_{in} $

W = W_out - W_in

(ID 15758)

$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R_C \ln( V_2 / V_1 )}}$

eta = ( T_2 - T_1 )/( T_1 + C_V *( T_2 - T_1 )/( n * R_C *log( V_2 / V_1 )))

La eficiencia ($\eta$) se define como la proporci n entre el trabajo efectivo ($W$) y el calor aportado al sistema ($Q$):

$ \eta \equiv \displaystyle\frac{ W }{ Q } $

donde el trabajo efectivo ($W$) est relacionado con el trabajo realizado por el sistema ($W_{out}$) y el trabajo realizado sobre el sistema ($W_{in}$) mediante:

$ W \equiv W_{out} - W_{in} $

mientras que el calor aportado al sistema ($Q$) est asociado con el calor suministrado ($Q_H$), cuyo valor se establece en:

$ Q \equiv W_{in} + Q_h $

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

y el trabajo realizado sobre el sistema ($W_{in}$) se asocia con la temperatura en estado 1 ($T_1$) por:

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

y el calor suministrado ($Q_H$) se relaciona con la capacidad calórica a volumen constante ($C_V$) en:

$ Q_h = C_V ( T_2 - T_1 )$

se puede calcular la eficiencia ($\eta$) resultando en:

$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R_C \ln( V_2 / V_1 )}}$

(ID 15759)

Ejemplos

Mecanismos

El ciclo de Stirling involucra cuatro fases principales: calentamiento, expansi n, enfriamiento y compresi n, realizadas en un ambiente sellado donde un gas como el helio o el hidr geno act a como fluido de trabajo.

Durante la fase de calentamiento, el gas se calienta a volumen constante, absorbiendo calor de una fuente externa lo que aumenta su temperatura y presi n. Esto es seguido por la fase de expansi n, donde el gas calentado se expande y realiza trabajo sobre un pist n u otro mecanismo, disminuyendo su temperatura y presi n pero convirtiendo el calor en energ a mec nica.

Luego ocurre la fase de enfriamiento a volumen constante. Aqu , el gas pierde calor, lo que disminuye su temperatura y presi n, prepar ndolo para la fase final. El regenerador juega un papel cr tico al absorber calor del gas, lo que conserva energ a y mejora la eficiencia.

El ciclo concluye con la compresi n del gas enfriado, lo cual requiere menos energ a de la que se produjo durante la expansi n. Esta compresi n aumenta la temperatura del gas, aunque no tanto como durante la fase inicial de calentamiento, y el ciclo comienza de nuevo.

El regenerador es vital durante todo este proceso, almacenando calor de la fase de enfriamiento y devolvi ndolo durante el calentamiento, reutilizando as la energ a dentro del sistema y aumentando significativamente la eficiencia t rmica del motor. Los motores Stirling son valorados por su operaci n silenciosa y la flexibilidad para usar cualquier fuente de calor, haci ndolos adaptables y beneficiosos para el medio ambiente en diversas aplicaciones.

(ID 15284)

Ciclo de Carnot

The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.

Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work. [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las m quinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)

(ID 11131)

Ciclo de Stirling: Diagrama presi n-volumen

El ciclo de Stirling [1] puede considerarse como una soluci n t cnica basada en el ciclo de Carnot, que consta de cuatro etapas bien definidas:

Etapa 1 a 2: Compresi n isot rmica $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_1)$.
Etapa 2 a 3: Calentamiento isoc rico $(p_2,V_2,T_1)\rightarrow(p_3,V_2,T_2)$.
Etapa 3 a 4: Expansi n isot rmica $(p_3,V_2,T_2)\rightarrow(p_4,V_1,T_2)$.
Etapa 4 a 1: Enfriamiento isoc rico $(p_4,V_1,T_2)\rightarrow(p_1,V_1,T_1)$.

Es importante destacar que este ciclo no involucra una etapa adiab tica; en cambio, se basa en el intercambio entre procesos isoc ricos (a volumen constante) y procesos isot rmicos (a temperatura constante).

Estas etapas se pueden visualizar en el siguiente diagrama:

[1] "An Economical Engine for the Purpose of Pumping Water by the Expansive Force of Steam" (Un motor econ mico para bombear agua mediante la fuerza expansiva del vapor), Robert Stirling, British Patent No. 4081 de 1816.

(ID 15362)

Ciclo de Stirling 1 a 2

$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$

Si la presión ($p$) se obtiene utilizando la constante universal de los gases ($R_C$), el número de moles ($n$) y la temperatura absoluta ($T$) con la ecuaci n de los gases

$ p V = n R_C T $

la integral para la temperatura absoluta ($T$) es igual a la temperatura en estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Por lo tanto,

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

(ID 15760)

Ciclo de Stirling 2 a 3

Al agregar el calor suministrado ($Q_H$) cuando el volumen ($V$) es igual al ERROR:8497,0 La temperatura absoluta ($T$) aumenta de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:

$ dU = C_V \Delta T $

esto nos lleva a la expresi n:

$ Q_h = C_V ( T_2 - T_1 )$

(ID 15761)

Ciclo de Stirling 3 a 4

$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$

Si la presión ($p$) se obtiene mediante la constante universal de los gases ($R_C$), el número de moles ($n$), y la temperatura absoluta ($T$) usando la ecuaci n de los gases

$ p V = n R_C T $

se obtiene la integral para la temperatura absoluta ($T$) igual a la temperatura en estado 1 ($T_1$).

$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$

Por lo tanto,

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

(ID 15762)

Ciclo de Stirling 4 a 1

Al eliminar el calor absorbido ($Q_C$) cuando el volumen ($V$) es igual al ERROR:8498,0 La temperatura absoluta ($T$) aumenta de la temperatura en estado 1 ($T_1$) a la temperatura en estado 2 ($T_2$). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:

$ dU = C_V \Delta T $

esto nos lleva a la expresi n:

$ Q_c = C_V ( T_1 - T_2 )$

(ID 15763)

Rendimiento de ciclo de Stirling

La eficiencia ($\eta$) se define como la proporci n entre el trabajo efectivo ($W$) y el calor aportado al sistema ($Q$):

$ \eta \equiv \displaystyle\frac{ W }{ Q } $

donde el trabajo efectivo ($W$) est relacionado con el trabajo realizado por el sistema ($W_{out}$) y el trabajo realizado sobre el sistema ($W_{in}$) mediante:

$ W \equiv W_{out} - W_{in} $

mientras que el calor aportado al sistema ($Q$) est asociado con el calor suministrado ($Q_H$), cuyo valor se establece en:

$ Q \equiv W_{in} + Q_h $

$ W_{out} = n R_C T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

y el trabajo realizado sobre el sistema ($W_{in}$) se asocia con la temperatura en estado 1 ($T_1$) por:

$ W_{in} = n R_C T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$

y el calor suministrado ($Q_H$) se relaciona con la capacidad calórica a volumen constante ($C_V$) en:

$ Q_h = C_V ( T_2 - T_1 )$

se puede calcular la eficiencia ($\eta$) resultando en:

$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R_C \ln( V_2 / V_1 )}}$

(ID 15764)

Modelo

(ID 15343)

ID:(1485, 0)