Usuario:
El Ciclo de Carnot
Storyboard 
El ciclo de Carnot es un ciclo genérico en el espacio presión-volumen que muestra como en principio se puede construir una maquina termodinamica que convierte el flujo de calor en trabajo mecanico.
ID:(1488, 0)
Mecanismos
Concepto
El ciclo consta de cuatro procesos reversibles: dos isotérmicos (temperatura constante) y dos adiabáticos (sin intercambio de calor). Durante la expansión isotérmica, el sistema (típicamente un gas) absorbe calor de un reservorio de alta temperatura, expandiéndose y realizando trabajo sobre el entorno. Esto es seguido por una expansión adiabática donde el sistema continúa realizando trabajo pero sin intercambiar calor, lo que provoca que se enfríe. El gas luego experimenta una compresión isotérmica, liberando calor a un reservorio más frío mientras se realiza trabajo sobre el gas para comprimirlo. El ciclo concluye con una compresión adiabática, que aumenta aún más la temperatura del gas, devolviéndolo a su estado original.
La belleza del ciclo de Carnot radica en su simplicidad y en la perspectiva que ofrece sobre los límites de eficiencia para todos los motores basados en calor. La eficiencia de un motor de Carnot depende únicamente de las temperaturas de los reservorios caliente y frío y es independiente de la sustancia de trabajo o los detalles del proceso en sí. Esta eficiencia se expresa como la relación entre la diferencia de temperaturas entre los reservorios y la temperatura más alta, mostrando que ningún motor real que opere entre dos reservorios de calor puede ser más eficiente que un motor de Carnot operando entre los mismos reservorios.
ID:(15281, 0)
Ciclo de Carnot: esquema de una maquina
Concepto
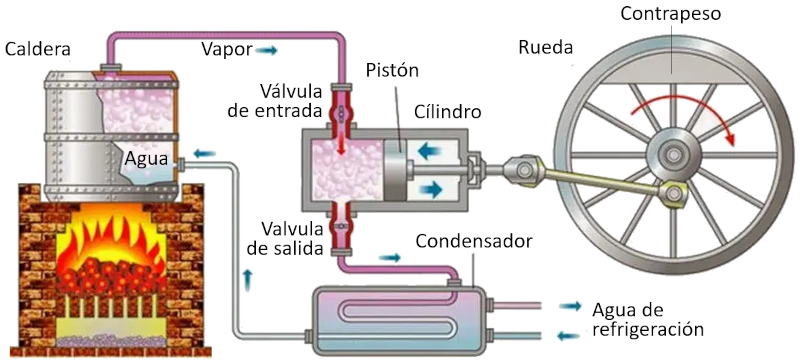
En una máquina que utiliza el concepto de Carnot, se llevan a cabo los siguientes procesos:
• El reservorio con la temperatura más alta se crea mediante un horno.
• El reservorio con la temperatura más baja se crea mediante un sistema de refrigeración.
• El vapor generado desde el reservorio se expande en forma de gas, desplazando el pistón y elevando la masa de compensación. En la primera etapa isotérmica, la primera válvula está abierta mientras que la segunda está cerrada. En la segunda etapa del proceso, se cierra la primera válvula y la expansión continúa de manera adiabática.
• En la tercera etapa, se abre la segunda válvula y con ayuda de la masa de compensación, el pistón regresa y el gas es expulsado de forma isotérmica. En la cuarta etapa, se cierra la válvula y el proceso concluye de manera adiabática.
ID:(11134, 0)
Ciclo de Carnot
Concepto
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:
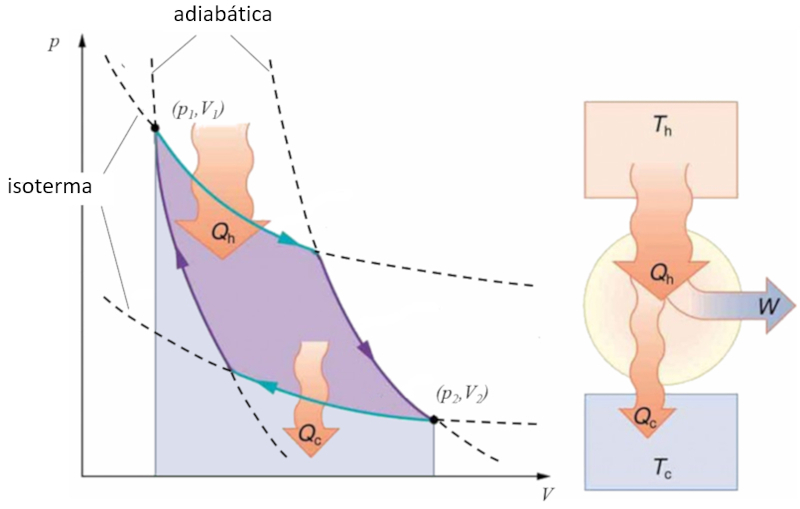
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las máquinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Aplicación en diagrama presión-volumen simple
Concepto
El ciclo de Carnot se describe de manera sencilla como un ciclo en el que se trabaja alternativamente de forma isotérmica y adiabática. En particular, se estudian los diagramas de presión-volumen y temperatura-entropía. En el primer caso, se pueden identificar las cuatro etapas que se llevan a cabo:
Etapa 1 a 2: Expansión isotérmica.
Etapa 2 a 3: Expansión adiabática.
Etapa 3 a 4: Compresión isotérmica.
Etapa 4 a 1: Compresión adiabática.
Estas etapas se representan a continuación:
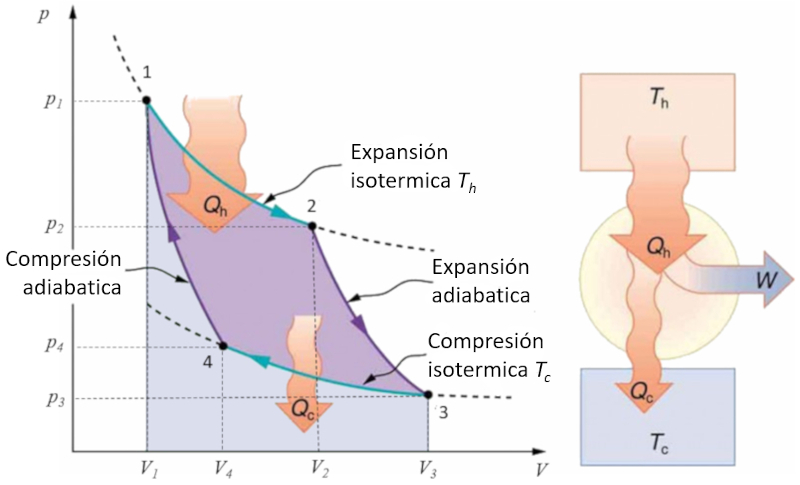
En el diagrama adjunto se muestra el flujo de energía, donde el calor suministrado ($Q_H$) (caliente) sale del baño a la temperatura alta ($T_H$), ingresa al sistema, se realiza un trabajo $W$, mientras que el complemento ERROR:8171,0 (frío) es absorbido por el baño a la temperatura baja ($T_C$).
ID:(11132, 0)
Aplicación en diagrama temperatura-entropía simple
Concepto
El ciclo de Carnot se describe de forma sencilla como un ciclo en el que se trabaja alternadamente de manera isotérmica y adiabática. En particular, se estudian los diagramas de presión-volumen y temperatura-entropía. En el segundo caso, el diagrama se simplifica al pasar de etapas isotérmicas a etapas de entropía constante:
En el diagrama temperatura-entropía, las etapas de entropía constante se representan de la siguiente manera:
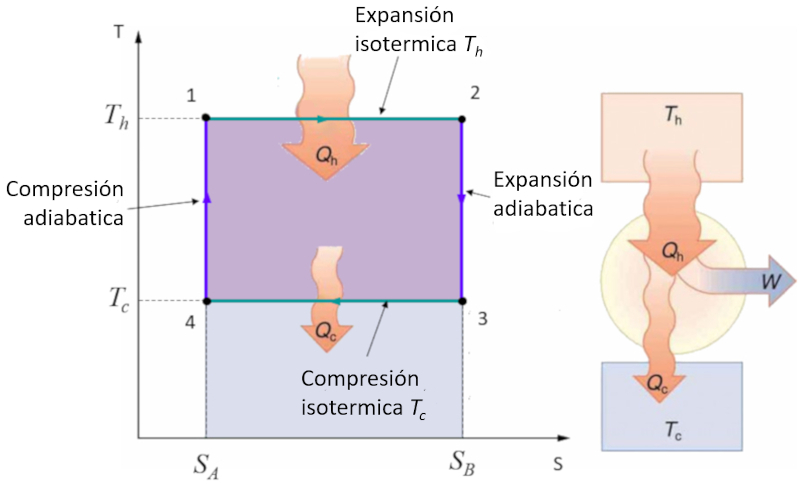
Durante estas etapas, la entropía ($S$) se mantiene constante, lo que significa que no hay transferencia de calor, mientras que la temperatura absoluta ($T$) puede variar. Esto simplifica la representación del ciclo y facilita un análisis más directo de las propiedades termodinámicas del sistema.
ID:(11133, 0)
Trabajo realizado
Concepto
Dado que el diferencial inexacto del trabajo ($\delta W$) se define en función de la presión ($p$) y la variación del volumen ($\Delta V$) como:
| $ \delta W = p dV $ |
Podemos calcular el trabajo efectivo ($W$) integrando a lo largo de las curvas del diagrama del ciclo:
$W = \displaystyle\oint pdV$
Utilizando la primera ley de la termodinámica con el diferencial de la energía interna ($dU$) y el diferencial inexacto del calor ($\delta Q$):
| $ dU = \delta Q - \delta W $ |
Y considerando el recorrido en el diagrama de la temperatura absoluta ($T$) y la entropía ($S$), obtenemos con la variación de la entropía ($dS$):
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
Dado que la integral a lo largo de un camino cerrado de un diferencial exacto es igual a cero, tenemos:
| $ W = \displaystyle\oint T dS$ |
ID:(10264, 0)
Rendimiento en función de calores
Concepto
Teniendo en cuenta que la eficiencia ($\eta$) con el trabajo efectivo ($W$) y el calor suministrado ($Q_H$) es
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
puede ser sustituido por el trabajo efectivo ($W$) que junto a el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) resulta en
| $ W = Q_H - Q_C $ |
obteniendo la siguiente relación:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(10262, 0)
Rendimiento en función de las temperaturas
Concepto
La eficiencia ($\eta$) es una función de el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) expresada como:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Podemos reemplazar el calor suministrado ($Q_H$) en función de la temperatura baja ($T_C$), la entropía baja ($S_C$) y la entropía alta ($S_H$) como:
| $ Q_C = T_C ( S_H - S_C ) $ |
Y utilizando la temperatura alta ($T_H$) como:
| $ Q_H = T_H ( S_H - S_C ) $ |
Si realizamos estos reemplazos, obtenemos:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(10260, 0)
El Ciclo de Carnot
Modelo
El ciclo de Carnot es un ciclo genérico en el espacio presión-volumen que muestra como en principio se puede construir una maquina termodinamica que convierte el flujo de calor en trabajo mecanico.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 11135)
La eficiencia ($\eta$) es una funci n de el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) expresada como:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Podemos reemplazar el calor suministrado ($Q_H$) en funci n de la temperatura baja ($T_C$), la entropía baja ($S_C$) y la entropía alta ($S_H$) como:
| $ Q_C = T_C ( S_H - S_C ) $ |
Y utilizando la temperatura alta ($T_H$) como:
| $ Q_H = T_H ( S_H - S_C ) $ |
Si realizamos estos reemplazos, obtenemos:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
(ID 11136)
Dado que el trabajo efectivo ($W$) es igual a la integral a lo largo de un camino cerrado en el espacio de la temperatura absoluta ($T$) y la entropía ($S$), tenemos:
| $ W = \displaystyle\oint T dS$ |
Consultando el gr fico temperatura-entrop a, podemos ver que el calor absorbido el calor suministrado ($Q_H$) es igual a la temperatura alta ($T_H$) debido a la diferencia de entrop a, es decir, la entropía alta ($S_H$) y la entropía baja ($S_C$):
| $ Q_H = T_H ( S_H - S_C ) $ |
(ID 11137)
Dado que el trabajo efectivo ($W$) es igual a la integral a lo largo de un camino cerrado en el espacio de la temperatura absoluta ($T$) y la entropía ($S$), tenemos:
| $ W = \displaystyle\oint T dS$ |
Consultando el gr fico temperatura-entrop a, podemos ver que el calor absorbido el calor absorbido ($Q_C$) es igual a la temperatura baja ($T_C$) debido a la diferencia de entrop a, es decir, la entropía alta ($S_H$) y la entropía baja ($S_C$):
| $ Q_C = T_C ( S_H - S_C ) $ |
(ID 11138)
Teniendo en cuenta que la eficiencia ($\eta$) con el trabajo efectivo ($W$) y el calor suministrado ($Q_H$) es
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
puede ser sustituido por el trabajo efectivo ($W$) que junto a el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) resulta en
| $ W = Q_H - Q_C $ |
obteniendo la siguiente relaci n:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
(ID 11155)
Ejemplos
El ciclo consta de cuatro procesos reversibles: dos isot rmicos (temperatura constante) y dos adiab ticos (sin intercambio de calor). Durante la expansi n isot rmica, el sistema (t picamente un gas) absorbe calor de un reservorio de alta temperatura, expandi ndose y realizando trabajo sobre el entorno. Esto es seguido por una expansi n adiab tica donde el sistema contin a realizando trabajo pero sin intercambiar calor, lo que provoca que se enfr e. El gas luego experimenta una compresi n isot rmica, liberando calor a un reservorio m s fr o mientras se realiza trabajo sobre el gas para comprimirlo. El ciclo concluye con una compresi n adiab tica, que aumenta a n m s la temperatura del gas, devolvi ndolo a su estado original.
La belleza del ciclo de Carnot radica en su simplicidad y en la perspectiva que ofrece sobre los l mites de eficiencia para todos los motores basados en calor. La eficiencia de un motor de Carnot depende nicamente de las temperaturas de los reservorios caliente y fr o y es independiente de la sustancia de trabajo o los detalles del proceso en s . Esta eficiencia se expresa como la relaci n entre la diferencia de temperaturas entre los reservorios y la temperatura m s alta, mostrando que ning n motor real que opere entre dos reservorios de calor puede ser m s eficiente que un motor de Carnot operando entre los mismos reservorios.
(ID 15281)
En una m quina que utiliza el concepto de Carnot, se llevan a cabo los siguientes procesos:
• El reservorio con la temperatura m s alta se crea mediante un horno.
• El reservorio con la temperatura m s baja se crea mediante un sistema de refrigeraci n.
• El vapor generado desde el reservorio se expande en forma de gas, desplazando el pist n y elevando la masa de compensaci n. En la primera etapa isot rmica, la primera v lvula est abierta mientras que la segunda est cerrada. En la segunda etapa del proceso, se cierra la primera v lvula y la expansi n contin a de manera adiab tica.
• En la tercera etapa, se abre la segunda v lvula y con ayuda de la masa de compensaci n, el pist n regresa y el gas es expulsado de forma isot rmica. En la cuarta etapa, se cierra la v lvula y el proceso concluye de manera adiab tica.
(ID 11134)
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work. [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las m quinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
(ID 11131)
El ciclo de Carnot se describe de manera sencilla como un ciclo en el que se trabaja alternativamente de forma isot rmica y adiab tica. En particular, se estudian los diagramas de presi n-volumen y temperatura-entrop a. En el primer caso, se pueden identificar las cuatro etapas que se llevan a cabo:
Etapa 1 a 2: Expansi n isot rmica.
Etapa 2 a 3: Expansi n adiab tica.
Etapa 3 a 4: Compresi n isot rmica.
Etapa 4 a 1: Compresi n adiab tica.
Estas etapas se representan a continuaci n:
En el diagrama adjunto se muestra el flujo de energ a, donde el calor suministrado ($Q_H$) (caliente) sale del ba o a la temperatura alta ($T_H$), ingresa al sistema, se realiza un trabajo $W$, mientras que el complemento ERROR:8171,0 (fr o) es absorbido por el ba o a la temperatura baja ($T_C$).
(ID 11132)
El ciclo de Carnot se describe de forma sencilla como un ciclo en el que se trabaja alternadamente de manera isot rmica y adiab tica. En particular, se estudian los diagramas de presi n-volumen y temperatura-entrop a. En el segundo caso, el diagrama se simplifica al pasar de etapas isot rmicas a etapas de entrop a constante:
En el diagrama temperatura-entrop a, las etapas de entrop a constante se representan de la siguiente manera:
Durante estas etapas, la entropía ($S$) se mantiene constante, lo que significa que no hay transferencia de calor, mientras que la temperatura absoluta ($T$) puede variar. Esto simplifica la representaci n del ciclo y facilita un an lisis m s directo de las propiedades termodin micas del sistema.
(ID 11133)
Dado que el diferencial inexacto del trabajo ($\delta W$) se define en funci n de la presión ($p$) y la variación del volumen ($\Delta V$) como:
| $ \delta W = p dV $ |
Podemos calcular el trabajo efectivo ($W$) integrando a lo largo de las curvas del diagrama del ciclo:
$W = \displaystyle\oint pdV$
Utilizando la primera ley de la termodin mica con el diferencial de la energía interna ($dU$) y el diferencial inexacto del calor ($\delta Q$):
| $ dU = \delta Q - \delta W $ |
Y considerando el recorrido en el diagrama de la temperatura absoluta ($T$) y la entropía ($S$), obtenemos con la variación de la entropía ($dS$):
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
Dado que la integral a lo largo de un camino cerrado de un diferencial exacto es igual a cero, tenemos:
| $ W = \displaystyle\oint T dS$ |
(ID 10264)
Teniendo en cuenta que la eficiencia ($\eta$) con el trabajo efectivo ($W$) y el calor suministrado ($Q_H$) es
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
puede ser sustituido por el trabajo efectivo ($W$) que junto a el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) resulta en
| $ W = Q_H - Q_C $ |
obteniendo la siguiente relaci n:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
(ID 10262)
La eficiencia ($\eta$) es una funci n de el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) expresada como:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Podemos reemplazar el calor suministrado ($Q_H$) en funci n de la temperatura baja ($T_C$), la entropía baja ($S_C$) y la entropía alta ($S_H$) como:
| $ Q_C = T_C ( S_H - S_C ) $ |
Y utilizando la temperatura alta ($T_H$) como:
| $ Q_H = T_H ( S_H - S_C ) $ |
Si realizamos estos reemplazos, obtenemos:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
(ID 10260)
(ID 15340)
ID:(1488, 0)