Benützer:
Der Stirling-Zyklus
Storyboard 
Eine thermodynamische Maschine, die nicht auf interne Verbrennung angewiesen ist, sondern ausschließlich äußere Wärmezufuhr erhält. Durch diesen Prozess entsteht dennoch der typische Druck-Volumen-Zyklus, was es ermöglicht, die erzielte Effizienz zu modellieren und zu berechnen.
ID:(1485, 0)
Mechanismen
Iframe
Der Stirling-Zyklus umfasst vier Hauptphasen: Heizen, Expandieren, Kühlen und Komprimieren, die in einer abgedichteten Umgebung durchgeführt werden, in der ein Gas wie Helium oder Wasserstoff als Arbeitsmedium dient.
Während der Heizphase wird das Gas bei konstantem Volumen erhitzt, wobei es Wärme aus einer externen Quelle aufnimmt, was seine Temperatur und seinen Druck erhöht. Dies wird gefolgt von der Expansionsphase, in der das erhitzte Gas expandiert und Arbeit an einem Kolben oder einem anderen Mechanismus verrichtet, wobei seine Temperatur und sein Druck sinken, aber die Wärme in mechanische Energie umgewandelt wird.
Dann erfolgt die Kühlphase bei konstantem Volumen. Hier verliert das Gas Wärme, was seine Temperatur und seinen Druck verringert und es auf die letzte Phase vorbereitet. Der Regenerator spielt eine entscheidende Rolle, indem er Wärme aus dem Gas aufnimmt, was Energie spart und die Effizienz erhöht.
Der Zyklus endet mit der Kompression des abgekühlten Gases, die weniger Energie erfordert als die während der Expansion erzeugte. Diese Kompression erhöht die Temperatur des Gases, wenn auch nicht so stark wie in der anfänglichen Heizphase, und der Zyklus beginnt von neuem.
Der Regenerator ist während dieses gesamten Prozesses von entscheidender Bedeutung, da er Wärme aus der Kühlphase speichert und während der Heizphase zurückführt, wodurch Energie innerhalb des Systems wiederverwendet und die thermische Effizienz des Motors erheblich gesteigert wird. Stirlingmotoren sind wegen ihres leisen Betriebs und der Flexibilität, jede Wärmequelle zu nutzen, geschätzt, was sie anpassungsfähig und umweltfreundlich für verschiedene Anwendungen macht.
Mechanismen
ID:(15284, 0)
Carnot-Zyklus
Konzept
Sadi Carnot führte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem Wärme hinzugefügt und extrahiert wird, wie in der Abbildung dargestellt:
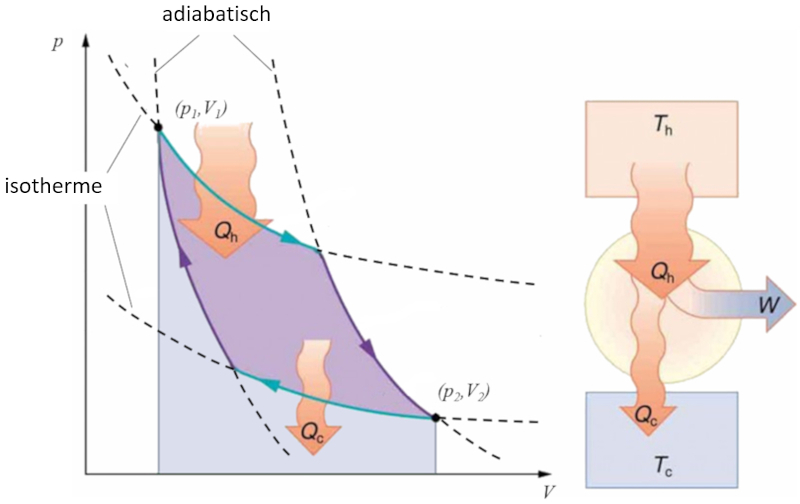
Die Fläche unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repräsentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) überzugehen. Umgekehrt repräsentiert die Fläche unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verläuft, die benötigte Energieentnahme, um vom Zustand ($p_2, V_2$) zurück zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Flächen entspricht dem von beiden Kurven umschlossenen Bereich und repräsentiert der Effektive Arbeit ($W$), den das System ausführen kann.
Carnot zeigte auch, dass gemäß dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte Wärme in Arbeit umzuwandeln.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexionen über die Triebkraft des Feuers und über Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, S. 393-457 (1872)
ID:(11131, 0)
Stirling-Zyklus: Druck-Volumen-Diagramm
Top
Der Stirling-Zyklus [1] kann als technische Lösung betrachtet werden, die auf dem Carnot-Zyklus basiert, der aus vier genau definierten Phasen besteht:
Phase 1 bis 2: Isotherme Kompression $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_1)$.
Phase 2 bis 3: Isokorische Erwärmung $(p_2,V_2,T_1)\rightarrow(p_3,V_2,T_2)$.
Phase 3 bis 4: Isotherme Expansion $(p_3,V_2,T_2)\rightarrow(p_4,V_1,T_2)$.
Phase 4 bis 1: Isokorisches Abkühlen $(p_4,V_1,T_2)\rightarrow(p_1,V_1,T_1)$.
Es ist wichtig zu betonen, dass dieser Zyklus keine adiabatische Phase beinhaltet; stattdessen basiert er auf dem Austausch zwischen isochoren Prozessen (bei konstantem Volumen) und isothermen Prozessen (bei konstanter Temperatur).
Diese Phasen können im folgenden Diagramm visualisiert werden:
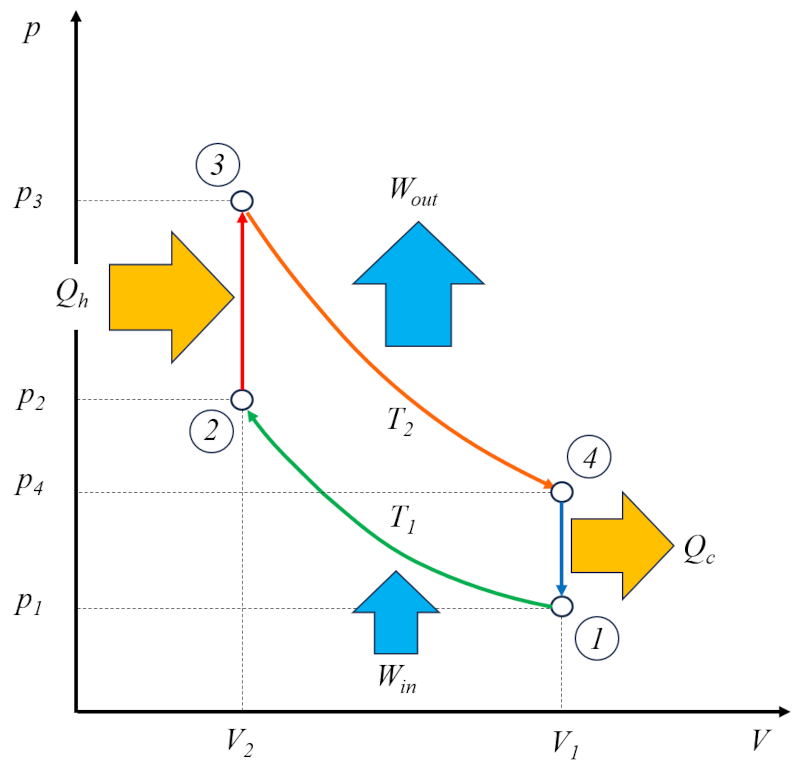
[1] "An Economical Engine for the Purpose of Pumping Water by the Expansive Force of Steam" (Ein wirtschaftlicher Motor zum Zwecke der Wasserförderung durch die expansive Kraft von Dampf), Robert Stirling, Britisches Patent Nr. 4081 von 1816.
ID:(15362, 0)
Stirling-Zyklus 1 bis 2
Konzept
In der ersten Stufe der Anzahl der Mol ($n$) wird das Gas mit der Am System durchgeführte Arbeiten ($W_{in}$) von der Erweitertes Volumen ($V_1$) auf der Komprimiertes Volumen ($V_2$) isotherm auf die Temperatur im Zustand 1 ($T_1$) mit der Anzahl der Mol ($n$) und die Druck ($p$) berechnet, das von der Erweitertes Volumen ($V_1$) bis der Komprimiertes Volumen ($V_2$) in der Volumen ($V$) integriert ist:
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Wenn die Druck ($p$) mit Hilfe von die Universelle Gas Konstante ($R$), der Anzahl der Mol ($n$) und die Absolute Temperatur ($T$) mithilfe der Gasgleichung
| $ p V = n R T $ |
erhalten wird, ergibt sich das Integral für die Absolute Temperatur ($T$) als die Temperatur im Zustand 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Daher ergibt sich:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15760, 0)
Stirling-Zyklus 2 bis 3
Konzept
In der zweiten Stufe wird der Wärme zugeführt ($Q_H$) hinzugefügt, was abhängig von die Wärmekapazität bei konstantem Volumen ($C_V$) die Temperatur von die Temperatur im Zustand 1 ($T_1$) auf die Temperatur im Zustand 2 ($T_2$) erhöht:
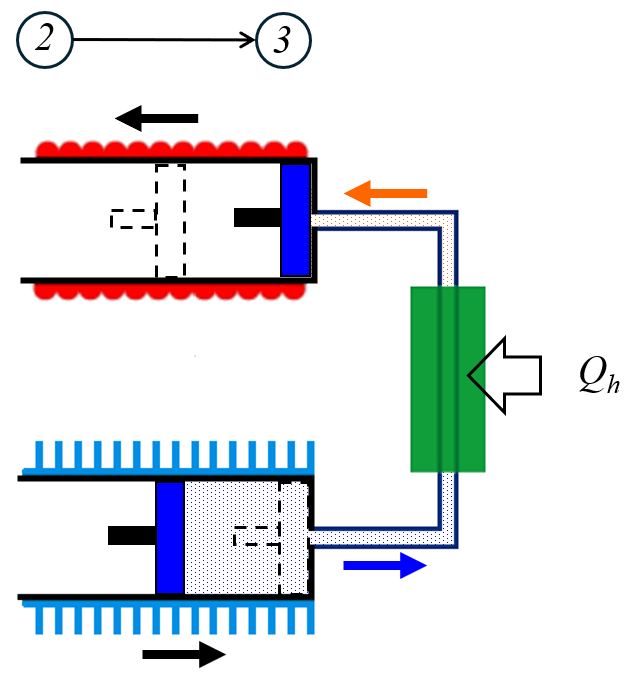
Durch die Zufuhr von der Wärme zugeführt ($Q_H$) steigt die Temperatur des Gases von $T_2$ auf $T_3$ in einem isochoren Prozess (bei konstantem Volumen). Dies bedeutet, dass wir die Beziehung für ($$) mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden können, die durch die folgende Gleichung ausgedrückt wird:
| $ dU = C_V \Delta T $ |
Dies führt zu den Werten von die Temperatur im Zustand 2 ($T_2$) und die Temperatur im Zustand 3 ($T_3$) wie folgt:
| $ Q_h = C_V ( T_2 - T_1 )$ |
ID:(15761, 0)
Stirling-Zyklus 3 bis 4
Konzept
In der dritten Stufe der Anzahl der Mol ($n$) dehnt sich das Gas auf der Vom System ausgeführte Arbeit ($W_{out}$) aus, während sich das Volumen isotherm von der Komprimiertes Volumen ($V_2$) auf der Erweitertes Volumen ($V_1$) ausdehnt var>8490:
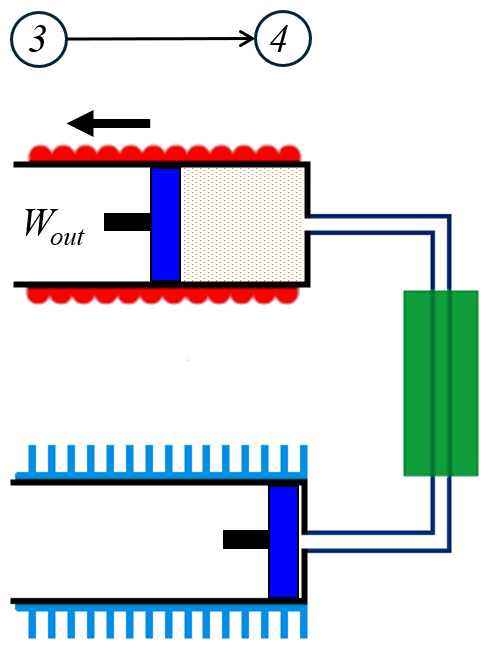
Die Arbeit wird durch die Integration von der Vom System ausgeführte Arbeit ($W_{out}$) mit die Druck ($p$) berechnet, die von ($$) bis der Erweitertes Volumen ($V_1$) in der Komprimiertes Volumen ($V_2$) integriert ist:
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Wenn die Druck ($p$) mit Hilfe der Gleichung für Gase, nämlich
| $ p V = n R T $ |
durch die Universelle Gas Konstante ($R$), der Anzahl der Mol ($n$) und die Absolute Temperatur ($T$) erhalten wird, ergibt sich das Integral für die Absolute Temperatur ($T$) als die Temperatur im Zustand 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Daher ergibt sich:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15762, 0)
Stirling-Zyklus 4 bis 1
Konzept
In der vierten Stufe wird der Absorbierte Wärme ($Q_C$) reduziert, wodurch, abhängig von die Wärmekapazität bei konstantem Volumen ($C_V$), die Temperatur von die Temperatur im Zustand 2 ($T_2$) auf die Temperatur im Zustand 1 ($T_1$) sinkt :
 $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
Beim Entfernen von der Absorbierte Wärme ($Q_C$), wenn der Volumen ($V$) gleich Komprimiertes Volumen ($V_2$) ist, erhöht sich die Absolute Temperatur ($T$) von die Temperatur im Zustand 1 ($T_1$) auf die Temperatur im Zustand 2 ($T_2$). Dies impliziert, dass wir die Beziehung für ($$) mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden können, die durch die Gleichung ausgedrückt wird:
| $ dU = C_V \Delta T $ |
dies führt uns zu dem Ausdruck:
| $ Q_c = C_V ( T_1 - T_2 )$ |
ID:(15763, 0)
Leistung des Stirling-Zyklus
Konzept
Die Leistungsfähigkeit ($\eta$) wird als das Verhältnis von der Effektive Arbeit ($W$) zu der Wärme trug zum System bei ($Q$) definiert:
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
wobei der Effektive Arbeit ($W$) in Beziehung zu der Vom System ausgeführte Arbeit ($W_{out}$) und der Am System durchgeführte Arbeiten ($W_{in}$) steht durch:
| $ W \equiv W_{out} - W_{in} $ |
während der Wärme trug zum System bei ($Q$) mit der Wärme zugeführt ($Q_H$) verbunden ist, was wie folgt definiert wird:
| $ Q \equiv W_{in} + Q_h $ |
Da der Vom System ausgeführte Arbeit ($W_{out}$) in Beziehung zu der Anzahl der Mol ($n$), die Temperatur im Zustand 2 ($T_2$), der Erweitertes Volumen ($V_1$), der Komprimiertes Volumen ($V_2$) und die Universelle Gas Konstante ($R$) steht durch:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
und der Am System durchgeführte Arbeiten ($W_{in}$) mit die Temperatur im Zustand 1 ($T_1$) verbunden ist durch:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
und der Wärme zugeführt ($Q_H$) mit die Wärmekapazität bei konstantem Volumen ($C_V$) verbunden ist durch:
| $ Q_h = C_V ( T_2 - T_1 )$ |
kann die Leistungsfähigkeit ($\eta$) berechnet werden, was zu folgendem Ergebnis führt:
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
ID:(15764, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$
eta = ( T_2 - T_1 )/( T_1 + C_V *( T_2 - T_1 )/( n * R *log( V_2 / V_1 )))
$ \eta \equiv \displaystyle\frac{ W }{ Q } $
eta = W / Q
$ Q \equiv W_{in} + Q_h $
Q = W_in + Q_h
$ Q_c = C_V ( T_1 - T_2 )$
Q_C = C_V *( T_1 - T_2 )
$ Q_h = C_V ( T_2 - T_1 )$
Q_H = C_V *( T_2 - T_1 )
$ W \equiv W_{out} - W_{in} $
W = W_out - W_in
$ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$
W_in = n * R * T_1 * log( V_2 / V_1 )
$ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$
W_out = n * R * T_2 * log( V_2 / V_1 )
ID:(15343, 0)
Dem System wird Wärme zugeführt
Gleichung
Das hinzuzufügende der Wärme zugeführt ($Q_H$) hängt von die Wärmekapazität bei konstantem Volumen ($C_V$) und dem Temperaturunterschied von die Temperatur im Zustand 1 ($T_1$) zu die Temperatur im Zustand 2 ($T_2$) ab:
| $ Q_h = C_V ( T_2 - T_1 )$ |
Durch die Zufuhr von der Wärme zugeführt ($Q_H$) steigt die Temperatur des Gases von $T_2$ auf $T_3$ in einem isochoren Prozess (bei konstantem Volumen). Dies bedeutet, dass wir die Beziehung für ($$) mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden können, die durch die folgende Gleichung ausgedrückt wird:
| $ dU = C_V \Delta T $ |
Dies führt zu den Werten von die Temperatur im Zustand 2 ($T_2$) und die Temperatur im Zustand 3 ($T_3$) wie folgt:
| $ Q_h = C_V ( T_2 - T_1 )$ |
ID:(15363, 0)
Isotherme Expansion
Gleichung
Der Vom System ausgeführte Arbeit ($W_{out}$) ist mit der Anzahl der Mol ($n$), die Universelle Gas Konstante ($R$), die Temperatur im Zustand 2 ($T_2$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) gleich:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
Die Arbeit wird durch die Integration von der Vom System ausgeführte Arbeit ($W_{out}$) mit die Druck ($p$) berechnet, die von ($$) bis der Erweitertes Volumen ($V_1$) in der Komprimiertes Volumen ($V_2$) integriert ist:
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Wenn die Druck ($p$) mit Hilfe der Gleichung für Gase, nämlich
| $ p V = n R T $ |
durch die Universelle Gas Konstante ($R$), der Anzahl der Mol ($n$) und die Absolute Temperatur ($T$) erhalten wird, ergibt sich das Integral für die Absolute Temperatur ($T$) als die Temperatur im Zustand 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Daher ergibt sich:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15366, 0)
Dem System wird Wärme entzogen
Gleichung
Das hinzuzufügende der Absorbierte Wärme ($Q_C$) hängt von die Wärmekapazität bei konstantem Volumen ($C_V$) und dem Temperaturunterschied von die Temperatur im Zustand 2 ($T_2$) zu die Temperatur im Zustand 1 ($T_1$) ab:
| $ Q_c = C_V ( T_1 - T_2 )$ |
Beim Entfernen von der Absorbierte Wärme ($Q_C$), wenn der Volumen ($V$) gleich Komprimiertes Volumen ($V_2$) ist, erhöht sich die Absolute Temperatur ($T$) von die Temperatur im Zustand 1 ($T_1$) auf die Temperatur im Zustand 2 ($T_2$). Dies impliziert, dass wir die Beziehung für ($$) mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden können, die durch die Gleichung ausgedrückt wird:
| $ dU = C_V \Delta T $ |
dies führt uns zu dem Ausdruck:
| $ Q_c = C_V ( T_1 - T_2 )$ |
ID:(15364, 0)
Isotherme Kompression
Gleichung
Der Am System durchgeführte Arbeiten ($W_{in}$) ist mit der Anzahl der Mol ($n$), die Universelle Gas Konstante ($R$), die Temperatur im Zustand 1 ($T_1$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) gleich:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
Die Arbeit wird mithilfe des Integrals von der Am System durchgeführte Arbeiten ($W_{in}$) mit der Anzahl der Mol ($n$) und die Druck ($p$) berechnet, das von der Erweitertes Volumen ($V_1$) bis der Komprimiertes Volumen ($V_2$) in der Volumen ($V$) integriert ist:
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Wenn die Druck ($p$) mit Hilfe von die Universelle Gas Konstante ($R$), der Anzahl der Mol ($n$) und die Absolute Temperatur ($T$) mithilfe der Gasgleichung
| $ p V = n R T $ |
erhalten wird, ergibt sich das Integral für die Absolute Temperatur ($T$) als die Temperatur im Zustand 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Daher ergibt sich:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15365, 0)
Effektive Arbeit geliefert
Gleichung
Der Effektive Arbeit ($W$) besteht aus der Am System durchgeführte Arbeiten ($W_{in}$) und der Vom System ausgeführte Arbeit ($W_{out}$):
| $ W \equiv W_{out} - W_{in} $ |
.
ID:(15758, 0)
Wärme trug zum System bei
Gleichung
Der Wärme trug zum System bei ($Q$) besteht aus der Wärme zugeführt ($Q_H$) und der Am System durchgeführte Arbeiten ($W_{in}$):
| $ Q \equiv W_{in} + Q_h $ |
.
ID:(15757, 0)
Leistung
Gleichung
Die Leistungsfähigkeit ($\eta$) kann als der Prozentsatz definiert werden, den der Effektive Arbeit ($W$) in der Wärme trug zum System bei ($Q$) darstellt:
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
.
ID:(15756, 0)
Leistung des Stirling-Zyklus
Gleichung
Die Leistungsfähigkeit ($\eta$) des Stirling-Zyklus hängt von die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), der Erweitertes Volumen ($V_1$), der Komprimiertes Volumen ($V_2$), die Wärmekapazität bei konstantem Volumen ($C_V$), der Anzahl der Mol ($n$) und die Universelle Gas Konstante ($R$):
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
Die Leistungsfähigkeit ($\eta$) wird als das Verhältnis von der Effektive Arbeit ($W$) zu der Wärme trug zum System bei ($Q$) definiert:
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
wobei der Effektive Arbeit ($W$) in Beziehung zu der Vom System ausgeführte Arbeit ($W_{out}$) und der Am System durchgeführte Arbeiten ($W_{in}$) steht durch:
| $ W \equiv W_{out} - W_{in} $ |
während der Wärme trug zum System bei ($Q$) mit der Wärme zugeführt ($Q_H$) verbunden ist, was wie folgt definiert wird:
| $ Q \equiv W_{in} + Q_h $ |
Da der Vom System ausgeführte Arbeit ($W_{out}$) in Beziehung zu der Anzahl der Mol ($n$), die Temperatur im Zustand 2 ($T_2$), der Erweitertes Volumen ($V_1$), der Komprimiertes Volumen ($V_2$) und die Universelle Gas Konstante ($R$) steht durch:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
und der Am System durchgeführte Arbeiten ($W_{in}$) mit die Temperatur im Zustand 1 ($T_1$) verbunden ist durch:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
und der Wärme zugeführt ($Q_H$) mit die Wärmekapazität bei konstantem Volumen ($C_V$) verbunden ist durch:
| $ Q_h = C_V ( T_2 - T_1 )$ |
kann die Leistungsfähigkeit ($\eta$) berechnet werden, was zu folgendem Ergebnis führt:
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
.
ID:(15759, 0)