El Ciclo de Diesel
Storyboard 
El ciclo de Diesel corresponde a un motor de combustión interna en que el calentamiento ocurre a presión constante dejando expandir el gas en el encendiendo la mezcla.
ID:(1487, 0)
Mecanismos
Concepto 
El ciclo Diesel es un ciclo termodinámico que fundamenta el funcionamiento de los motores diésel, ampliamente utilizados en vehículos y maquinaria industrial. Desarrollado por Rudolf Diesel en la década de 1890, este ciclo se distingue del ciclo Otto de los motores de gasolina principalmente en su proceso de encendido. En el ciclo Diesel, el aire se introduce en el cilindro y se comprime a una relación mucho mayor que en los motores de gasolina, lo que eleva su temperatura hasta un punto que puede encender el combustible diésel sin necesidad de una bujía.
Durante el funcionamiento, el ciclo comienza con el pistón atrayendo aire mientras se mueve hacia abajo. Luego, el aire se comprime en el movimiento ascendente, aumentando su temperatura. En el pico de la fase de compresión, el combustible se inyecta en el aire comprimido y caliente en forma de una fina neblina, causando una ignición espontánea. La combustión empuja el pistón hacia abajo, generando energía. Finalmente, en la fase de escape, los gases de la combustión se expulsan cuando el pistón se mueve hacia arriba nuevamente, completando el ciclo.
Los motores diésel son reconocidos por su eficiencia y durabilidad. La alta relación de compresión no solo permite que el motor extraiga más energía del combustible, sino que también aumenta su eficiencia térmica, lo que significa que una mayor parte de la energía del combustible se convierte en trabajo mecánico. Los motores diésel generalmente ofrecen una mejor eficiencia de combustible y producen menos emisiones de CO2 por unidad de energía que sus contrapartes de gasolina, pero pueden emitir niveles más altos de otros contaminantes, como óxidos de nitrógeno y partículas.
ID:(15283, 0)
Ciclo de Carnot
Concepto 
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:
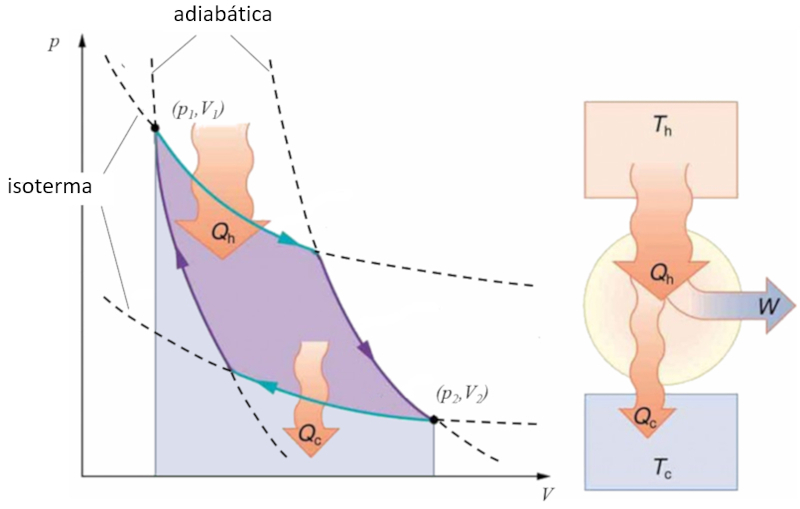
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.![]() [1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las máquinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las máquinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Ciclo de Diesel: Diagrama presión-volumen
Concepto 
Rudolf Diesel [1] se propuso crear un ciclo diferente al ciclo de Carnot con el objetivo de lograr una eficiencia superior en comparación con el ciclo de Otto. Este proceso se desarrolla en las siguientes etapas:
• Etapa 1 a 2: Compresión adiabática $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• Etapa 2 a 3: Calentamiento y expansión a presión constante $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• Etapa 3 a 4: Expansión adiabática $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• Etapa 4 a 1: Enfriamiento a volumen constante $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$
Estas etapas se ilustran a continuación:
La clave se encuentra en la etapa 2 a 3, donde la expansión ocurre a presión constante. La razón se hace evidente al examinar el gráfico:
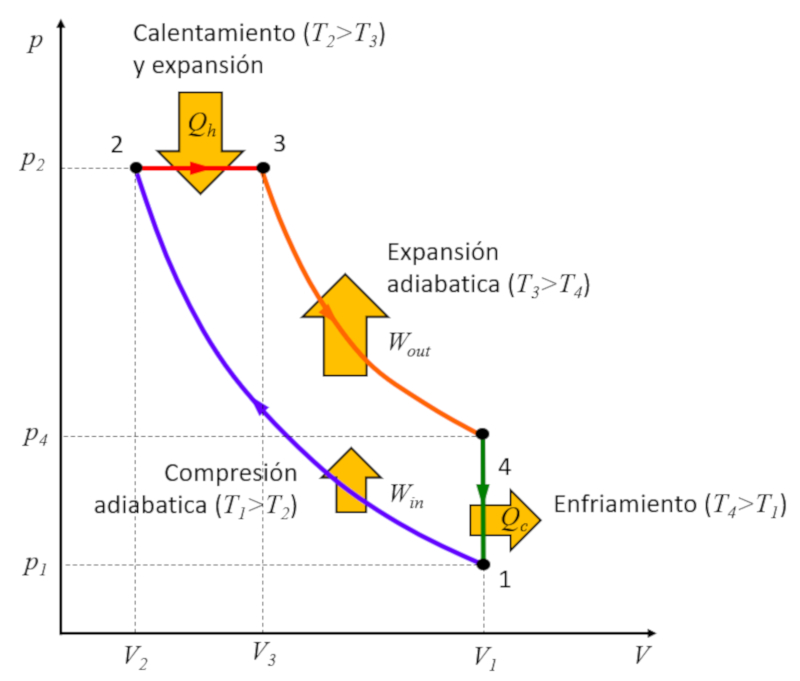
La energía ganada es igual al área encerrada dentro del ciclo, y al realizar la compresión a presión constante, esta área es mayor que en el caso de la compresión a volumen constante.![]() [1] "Verfahren zur Entwickelung eines rationellen Wärmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (Método para el desarrollo de un motor térmico racional que reemplace el motor de vapor y los motores de combustión contemporáneos), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)
[1] "Verfahren zur Entwickelung eines rationellen Wärmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (Método para el desarrollo de un motor térmico racional que reemplace el motor de vapor y los motores de combustión contemporáneos), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)
ID:(11141, 0)
Análisis de la eficiencia
Concepto 
Tanto el ciclo de Otto como el ciclo de Diesel dependen de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$). Sin embargo, en el caso del ciclo de Diesel, también depende de el indice adiabático ($\kappa$), cuyo valor es de 1.4.
En el caso del ciclo de Otto, la eficiencia se calcula en función de la temperatura utilizando la ecuación:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Mientras que en el ciclo de Diesel, la eficiencia se calcula en función de la temperatura utilizando la ecuación:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
La inclusión del factor $1/\kappa \sim 0.71$ en el ciclo de Diesel lo hace más eficiente en comparación con el ciclo de Otto para la misma configuración de temperaturas. Esto es la consecuencia directa de haber logrado aumentar el área encerrada en la curva que representa el ciclo en la representación presión y volumen.
ID:(11153, 0)
Expansión adiabática
Concepto 
Dado que en una expansión adiabática, el gas cumple con las relaciones el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$) expresadas como:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Podemos observar que en el cambio de estado desde el volumen intermedio ($V_3$) y la temperatura en estado 3 ($T_3$) a el volumen expandido ($V_1$) y la temperatura en estado 4 ($T_4$), se cumple la siguiente igualdad:
$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$
Utilizando la ecuación de el factor de expansibilidad ($r_E$):
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
Obtenemos:
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
ID:(15751, 0)
Compresión adiabática
Concepto 
Dado que en una expansión adiabática, el gas satisface las relaciones el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$), expresadas como:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Podemos notar que durante el cambio de estado desde el volumen expandido ($V_1$) y la temperatura en estado 1 ($T_1$) a el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$), se cumple la siguiente igualdad:
$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$
Usando la ecuación de el factor de compresibilidad ($r_C$):
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
Obtenemos:
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
ID:(15752, 0)
Calentamiento del gas
Concepto 
Como el calentamiento ocurre a presión constante, se aplica la ley de Charles que con el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$) es:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Podemos notar que durante el cambio de estado desde el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$) a el volumen intermedio ($V_3$) y la temperatura en estado 3 ($T_3$), se cumple la siguiente igualdad:
$\displaystyle\frac{ T_2 }{ V_2 }=\displaystyle\frac{ T_3 }{ V_3 }$
Usando la ecuación de el factor de compresibilidad ($r_C$) y el factor de expansibilidad ($r_E$):
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
podemos escribirlo como:
$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$
En resumen:
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
ID:(15753, 0)
Eficiencia en función de las temperaturas
Concepto 
La eficiencia ($\eta$) es una función el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) según:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
y las cantidad de el calor suministrado ($Q_H$) con la capacidad calórica a presión constante ($C_p$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) suministrado
| $ Q_H = C_p ( T_3 - T_2 )$ |
y con el calor absorbido ($Q_C$) con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) emitiendo
| $ Q_C = C_V ( T_4 - T_1 )$ |
Si se reemplaza ambas expresiones para el calor y se emplea la relación de el indice adiabático ($\kappa$):
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
se obtiene
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(15754, 0)
Eficiencia en función de los factores de compresión y expansión
Concepto 
El valor de la eficiencia ($\eta$) se puede calcular utilizando los valores el indice adiabático ($\kappa$), la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$) en la siguiente ecuación:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Además, las relaciones entre las temperaturas con el factor de compresibilidad ($r_C$) y el factor de expansibilidad ($r_E$) están definidas por las siguientes ecuaciones:
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
Adicionalmente, se utiliza el valor de el indice adiabático ($\kappa$) en la ecuación:
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
Estas ecuaciones nos permiten calcular el rendimiento de un proceso que sigue el ciclo de Diesel mediante la siguiente ecuación:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$ |
ID:(15755, 0)
El Ciclo de Diesel
Modelo 
El ciclo de Diesel corresponde a un motor de combustión interna en que el calentamiento ocurre a presión constante dejando expandir el gas en el encendiendo la mezcla.
Variables
Cálculos
Cálculos
Ecuaciones
Siguiendo una analog a al ERROR:5219,0 de l quidos y s lidos con la capacidad calórica ($C$) y la masa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe tambi n un calor específico de gases a volumen constante ($c_V$) para calentamiento bajo volumen constante con la capacidad calórica a volumen constante ($C_V$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
(ID 11113)
Siguiendo una analog a al ERROR:5219,0 de l quidos y s lidos con la capacidad calórica ($C$) y la masa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe tambi n un calor especifico a presión constante ($c_p$) para calentamiento bajo presi n constante con la capacidad calórica a presión constante ($C_p$):
| $ c_p =\displaystyle\frac{ C_p }{ M }$ |
(ID 11114)
Al suministrar el calor suministrado ($Q_H$), la temperatura del gas aumenta de $T_2$ a $T_3$ en un proceso isob rico (a presi n constante). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a presión constante ($C_p$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:
| $ \Delta Q = C_p \Delta T $ |
Esto nos lleva a los valores de la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) mediante la f rmula:
| $ Q_H = C_p ( T_3 - T_2 )$ |
(ID 11144)
Al retirar el calor absorbido ($Q_C$), la temperatura del gas aumenta de $T_1$ a $T_4$ en un proceso isob rico (a presi n constante). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:
| $ dU = C_V \Delta T $ |
Esto nos lleva a los valores de la temperatura en estado 1 ($T_1$) y la temperatura en estado 4 ($T_4$) mediante la f rmula:
| $ Q_C = C_V ( T_4 - T_1 )$ |
(ID 11145)
Dado que en una expansi n adiab tica, el gas satisface las relaciones el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$), expresadas como:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Podemos notar que durante el cambio de estado desde el volumen expandido ($V_1$) y la temperatura en estado 1 ($T_1$) a el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$), se cumple la siguiente igualdad:
$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$
Usando la ecuaci n de el factor de compresibilidad ($r_C$):
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
Obtenemos:
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
(ID 11148)
Dado que en una expansi n adiab tica, el gas cumple con las relaciones el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$) expresadas como:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Podemos observar que en el cambio de estado desde el volumen intermedio ($V_3$) y la temperatura en estado 3 ($T_3$) a el volumen expandido ($V_1$) y la temperatura en estado 4 ($T_4$), se cumple la siguiente igualdad:
$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$
Utilizando la ecuaci n de el factor de expansibilidad ($r_E$):
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
Obtenemos:
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
(ID 11149)
Como el calentamiento ocurre a presi n constante, se aplica la ley de Charles que con el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$) es:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Podemos notar que durante el cambio de estado desde el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$) a el volumen intermedio ($V_3$) y la temperatura en estado 3 ($T_3$), se cumple la siguiente igualdad:
$\displaystyle\frac{ T_2 }{ V_2 }=\displaystyle\frac{ T_3 }{ V_3 }$
Usando la ecuaci n de el factor de compresibilidad ($r_C$) y el factor de expansibilidad ($r_E$):
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
podemos escribirlo como:
$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$
En resumen:
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
(ID 11150)
El valor de la eficiencia ($\eta$) se puede calcular utilizando los valores el indice adiabático ($\kappa$), la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$) en la siguiente ecuaci n:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Adem s, las relaciones entre las temperaturas con el factor de compresibilidad ($r_C$) y el factor de expansibilidad ($r_E$) est n definidas por las siguientes ecuaciones:
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
Adicionalmente, se utiliza el valor de el indice adiabático ($\kappa$) en la ecuaci n:
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
Estas ecuaciones nos permiten calcular el rendimiento de un proceso que sigue el ciclo de Diesel mediante la siguiente ecuaci n:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$ |
(ID 11156)
En una expansi n adiab tica, el gas cumple con la relaci n que involucra el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
En este contexto, se pasa del punto inicial 3 al punto 4. Esto implica que durante la expansi n adiab tica, el estado del gas se modifica desde el volumen comprimido ($V_2$) y la temperatura en estado 3 ($T_3$) hasta el volumen expandido ($V_1$) y la temperatura en estado 4 ($T_4$), seg n se establece en:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
(ID 11159)
Dado que en una expansi n adiab tica, el gas satisface la relaci n con el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
En este caso, el punto inicial 1 al punto 2. Esto significa que durante la compresi n adiab tica, el estado del gas cambia de el volumen expandido ($V_1$) y la temperatura en estado 1 ($T_1$) a el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$) de acuerdo con:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
(ID 11160)
La eficiencia ($\eta$) es una funci n el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) seg n:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
y las cantidad de el calor suministrado ($Q_H$) con la capacidad calórica a presión constante ($C_p$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) suministrado
| $ Q_H = C_p ( T_3 - T_2 )$ |
y con el calor absorbido ($Q_C$) con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) emitiendo
| $ Q_C = C_V ( T_4 - T_1 )$ |
Si se reemplaza ambas expresiones para el calor y se emplea la relaci n de el indice adiabático ($\kappa$):
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
se obtiene
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
(ID 11164)
Ejemplos
El ciclo Diesel es un ciclo termodin mico que fundamenta el funcionamiento de los motores di sel, ampliamente utilizados en veh culos y maquinaria industrial. Desarrollado por Rudolf Diesel en la d cada de 1890, este ciclo se distingue del ciclo Otto de los motores de gasolina principalmente en su proceso de encendido. En el ciclo Diesel, el aire se introduce en el cilindro y se comprime a una relaci n mucho mayor que en los motores de gasolina, lo que eleva su temperatura hasta un punto que puede encender el combustible di sel sin necesidad de una buj a.
Durante el funcionamiento, el ciclo comienza con el pist n atrayendo aire mientras se mueve hacia abajo. Luego, el aire se comprime en el movimiento ascendente, aumentando su temperatura. En el pico de la fase de compresi n, el combustible se inyecta en el aire comprimido y caliente en forma de una fina neblina, causando una ignici n espont nea. La combusti n empuja el pist n hacia abajo, generando energ a. Finalmente, en la fase de escape, los gases de la combusti n se expulsan cuando el pist n se mueve hacia arriba nuevamente, completando el ciclo.
Los motores di sel son reconocidos por su eficiencia y durabilidad. La alta relaci n de compresi n no solo permite que el motor extraiga m s energ a del combustible, sino que tambi n aumenta su eficiencia t rmica, lo que significa que una mayor parte de la energ a del combustible se convierte en trabajo mec nico. Los motores di sel generalmente ofrecen una mejor eficiencia de combustible y producen menos emisiones de CO2 por unidad de energ a que sus contrapartes de gasolina, pero pueden emitir niveles m s altos de otros contaminantes, como xidos de nitr geno y part culas.
(ID 15283)
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:

The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.![]() [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las m quinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las m quinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
(ID 11131)
Rudolf Diesel [1] se propuso crear un ciclo diferente al ciclo de Carnot con el objetivo de lograr una eficiencia superior en comparaci n con el ciclo de Otto. Este proceso se desarrolla en las siguientes etapas:
• Etapa 1 a 2: Compresi n adiab tica $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• Etapa 2 a 3: Calentamiento y expansi n a presi n constante $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• Etapa 3 a 4: Expansi n adiab tica $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• Etapa 4 a 1: Enfriamiento a volumen constante $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$
Estas etapas se ilustran a continuaci n:
La clave se encuentra en la etapa 2 a 3, donde la expansi n ocurre a presi n constante. La raz n se hace evidente al examinar el gr fico:

La energ a ganada es igual al rea encerrada dentro del ciclo, y al realizar la compresi n a presi n constante, esta rea es mayor que en el caso de la compresi n a volumen constante.![]() [1] "Verfahren zur Entwickelung eines rationellen W rmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (M todo para el desarrollo de un motor t rmico racional que reemplace el motor de vapor y los motores de combusti n contempor neos), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)
[1] "Verfahren zur Entwickelung eines rationellen W rmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (M todo para el desarrollo de un motor t rmico racional que reemplace el motor de vapor y los motores de combusti n contempor neos), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)
(ID 11141)
Tanto el ciclo de Otto como el ciclo de Diesel dependen de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$). Sin embargo, en el caso del ciclo de Diesel, tambi n depende de el indice adiabático ($\kappa$), cuyo valor es de 1.4.
En el caso del ciclo de Otto, la eficiencia se calcula en funci n de la temperatura utilizando la ecuaci n:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Mientras que en el ciclo de Diesel, la eficiencia se calcula en funci n de la temperatura utilizando la ecuaci n:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
La inclusi n del factor $1/\kappa \sim 0.71$ en el ciclo de Diesel lo hace m s eficiente en comparaci n con el ciclo de Otto para la misma configuraci n de temperaturas. Esto es la consecuencia directa de haber logrado aumentar el rea encerrada en la curva que representa el ciclo en la representaci n presi n y volumen.
(ID 11153)
Dado que en una expansi n adiab tica, el gas cumple con las relaciones el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$) expresadas como:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Podemos observar que en el cambio de estado desde el volumen intermedio ($V_3$) y la temperatura en estado 3 ($T_3$) a el volumen expandido ($V_1$) y la temperatura en estado 4 ($T_4$), se cumple la siguiente igualdad:
$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$
Utilizando la ecuaci n de el factor de expansibilidad ($r_E$):
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
Obtenemos:
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
(ID 15751)
Dado que en una expansi n adiab tica, el gas satisface las relaciones el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$), expresadas como:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Podemos notar que durante el cambio de estado desde el volumen expandido ($V_1$) y la temperatura en estado 1 ($T_1$) a el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$), se cumple la siguiente igualdad:
$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$
Usando la ecuaci n de el factor de compresibilidad ($r_C$):
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
Obtenemos:
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
(ID 15752)
Como el calentamiento ocurre a presi n constante, se aplica la ley de Charles que con el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$) es:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Podemos notar que durante el cambio de estado desde el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$) a el volumen intermedio ($V_3$) y la temperatura en estado 3 ($T_3$), se cumple la siguiente igualdad:
$\displaystyle\frac{ T_2 }{ V_2 }=\displaystyle\frac{ T_3 }{ V_3 }$
Usando la ecuaci n de el factor de compresibilidad ($r_C$) y el factor de expansibilidad ($r_E$):
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
podemos escribirlo como:
$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$
En resumen:
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
(ID 15753)
La eficiencia ($\eta$) es una funci n el calor suministrado ($Q_H$) y el calor absorbido ($Q_C$) seg n:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
y las cantidad de el calor suministrado ($Q_H$) con la capacidad calórica a presión constante ($C_p$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) suministrado
| $ Q_H = C_p ( T_3 - T_2 )$ |
y con el calor absorbido ($Q_C$) con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) emitiendo
| $ Q_C = C_V ( T_4 - T_1 )$ |
Si se reemplaza ambas expresiones para el calor y se emplea la relaci n de el indice adiabático ($\kappa$):
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
se obtiene
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
(ID 15754)
El valor de la eficiencia ($\eta$) se puede calcular utilizando los valores el indice adiabático ($\kappa$), la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$) en la siguiente ecuaci n:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Adem s, las relaciones entre las temperaturas con el factor de compresibilidad ($r_C$) y el factor de expansibilidad ($r_E$) est n definidas por las siguientes ecuaciones:
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
Adicionalmente, se utiliza el valor de el indice adiabático ($\kappa$) en la ecuaci n:
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
Estas ecuaciones nos permiten calcular el rendimiento de un proceso que sigue el ciclo de Diesel mediante la siguiente ecuaci n:
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$ |
(ID 15755)
(ID 15342)
ID:(1487, 0)
