Usuario:


Distribuciones de Poisson
Storyboard

En el caso en que la probabilidad es muy pequeña la distribución binomial se reduce a una distribución de Poisson.

>Modelo

ID:(1555, 0)


Ejemplo comparación con distribución de Poisson
Definición

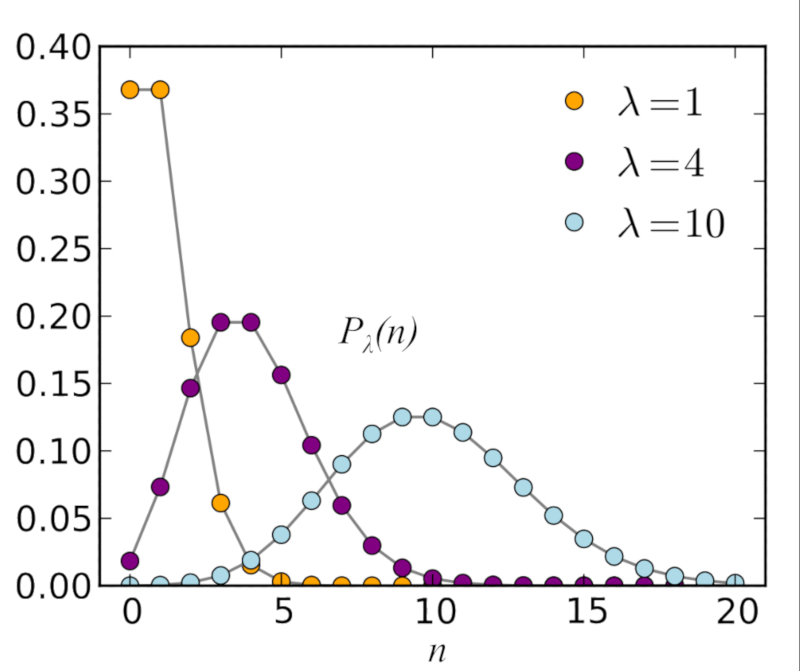
Si se estudia la distribución binomial para números grandes N y probabilidad muy pequeña p\ll 1 se puede aproximar mediante una distribución de Poisson. La comparación se puede realizar con el siguiente simulador:

ID:(7794, 0)


Distribuciones de Poisson
Descripción

En el caso en que la probabilidad es muy pequeña la distribución binomial se reduce a una distribución de Poisson.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\lambda$
lam
Desviación estándar de Poisson
-
$e^{-\lambda}$
elam
Exponential $e^{-\lambda}$
-
$N^n$
N^n
Exponential $N^n$
-
$n!$
n!
Factorial $n!$
-
$n$
n
Numero
-
$N$
N
Número total de pasos
-
$n$
n
Número totales de pasos a la derecha
-
$\lambda^n$
lambda_n
Power of lambda $\lambda^n$
-
$P_N(m)$
P_Nm
Probabilidad de hacer un numero de pasos hacia la derecha
-
$p$
p
Probabilidad de pasos hacia la derecha
-

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

Con la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$



con el n mero total de pasos es

$N=n_1+n_2$



y solo existe la probabilidad de ir a la derecha o a la izquierda, con se tiene para las probabilidades que

$p+q=1$



por lo que con se tiene la distribuci n binomial

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

(ID 8961)

Por ello expresiones como N!/(N-n)! para N grande (N\gg 1) y n chico (N\gg n) se pueden aproximar con

$u!\sim\sqrt{2\pi u}\left(\displaystyle\frac{u}{e}\right)^u$



con lo que se obtiene con N\gg n

\displaystyle\frac{N!}{(N-n)!}\sim\displaystyle\frac{\sqrt{2\pi N}}{\sqrt{2\pi (N-n)}}\displaystyle\frac{N^N}{(N-n)^{N-n}}\displaystyle\frac{e^{N-n}}{e^N}\sim N^n

osea

$N^n\sim\displaystyle\frac{N!}{(N-n)!}$

(ID 4738)

La desviaci n estandard de la distribuci n binomial en el l mite N grande y p peque o es

$\lambda=Np$

(ID 8964)

Con la aproximaci n

$N^n\sim\displaystyle\frac{N!}{(N-n)!}$



y empleando

$\lambda=Np$



se puede mostrar que

$\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n$

(ID 8969)

Como el exponencial se define como

$e^z\sim\left(1+\displaystyle\frac{z}{u}\right)^u$



y al introducir

$\lambda=Np$



se puede reemplazar z=-\lambda=-Np y u=N-n con N\gg n lo que resulta

$e^{-\lambda}\sim (1-p)^{N-n}$

(ID 8968)

Como la probabilidad de dar n pasos en una direcci n es

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$



para un n mero grande N y la probabilidad es muy peque a p\ll 1 se puede aproximar

$\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n$



y

$e^{-\lambda}\sim (1-p)^{N-n}$



la distribuci n binomial se reduce a una distribuci n de Poisson:

$ P_{\lambda}(n) =\displaystyle\frac{ \lambda ^ n }{ n! }e^{- \lambda }$

(ID 3369)

Si se estudia la distribuci n binomial para n meros grandes N y probabilidad muy peque a p\ll 1 se puede aproximar mediante una distribuci n de Poisson. La comparaci n se puede realizar con el siguiente simulador:

(ID 7794)

ID:(1555, 0)