Benützer:
Diagramm im Impuls-Positions-Raum $p-q$
Beschreibung
Eine Technik zur Analyse der Bewegung besteht darin, den Impuls in Abhängigkeit von der Position eines sich bewegenden Körpers darzustellen. Diese Darstellung ermöglicht es uns, zu untersuchen, wie sich der Impuls in Bezug auf die erreichte Position entwickelt.
Die Darstellung der Bewegung im Impuls-Positions-Raum $p-q$ ermöglicht es uns, die Entwicklung der Verschiebung zu analysieren und die Extrema in Position und Impuls hervorzuheben.
Im Falle einer periodischen Bewegung oder wenn wir den Hin- und Rückweg betrachten, kann dies wie folgt dargestellt werden:
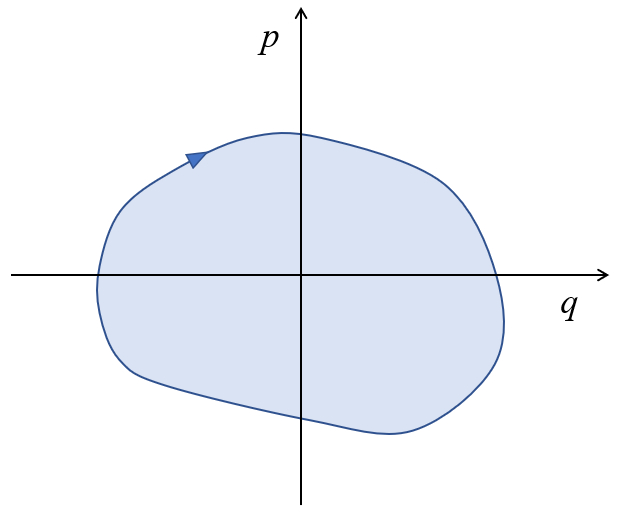
Zusätzlich kann man sehen, dass die Fläche, die von der Kurve eingeschlossen wird
$\displaystyle\int_{q_1}^{q_2} p dq = \displaystyle\int_{v_1}^{v_2} m v dv = \displaystyle\frac{1}{2} m v_2^2 - \displaystyle\frac{1}{2} m v_1^2$
der Energie des Systems entspricht.
Die von der Kurve im Impuls-Positions-Diagramm $p-q$ eingeschlossene Fläche entspricht der Energie des Systems.
ID:(1240, 0)
Kinetische Energie als Funktion des Moments
Gleichung
Die kinetische Energie einer Masse $m$
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
kann in Abhängigkeit vom Impuls ausgedrückt werden als
 $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
Da die kinetische Energie gleich ist
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
und der Impuls
| $ p = m_i v $ |
können wir es ausdrücken als
$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$
oder
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
ID:(4425, 0)
Moment als Funktion von Energie und potentieller Funktion
Gleichung
Wenn wir die Energie nach dem Impuls auflösen, erhalten wir die Ausdrücke für den positiven und negativen Impuls:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
Da die Energie im Allgemeinen die Summe aus kinetischer Energie
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
und potentieller Energie
$E=\displaystyle\frac{p^2}{2m}+U$
Wenn wir nach dem Impuls auflösen, ergibt sich der folgende Ausdruck:
| $ p =\pm\sqrt{2 m ( E - U )}$ |
ID:(4429, 0)
Teilchen unter Erdbeschleunigung in Darstellung $p-q$
Gleichung
Für den Fall eines Teilchens im Gravitationsfeld der Erde ist die Energie in Abhängigkeit vom Impuls $p$ und der Position $q$ gegeben durch
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
Da die kinetische Energie in Abhängigkeit vom Impuls ist
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
und die potenzielle Energie in Abhängigkeit von der Höhe ist
| $ V = m g z $ |
können wir, wenn wir die Höhe als Position ausdrücken
$h = q$
erhalten wir
| $ E =\displaystyle\frac{ p ^2}{2 m_i }+ m_g g q $ |
Die Gleichung kann adimensional dargestellt werden als
$y=\pm\sqrt{1-x}$
mit
$x=\displaystyle\frac{q}{mg/E}$
, und
$y=\displaystyle\frac{p}{\sqrt{2mE}}$
was unten dargestellt ist
ID:(4426, 0)
Harmonischer Oszillator (Feder), der $p-q$ darstellt
Gleichung
Für den Fall einer Masse, die mit einem Feder schwingt, ist die Energie als Funktion des Impulses $p$ und der Position $q$
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
Die kinetische Energie in Abhängigkeit vom Impuls ist gegeben durch
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
und die potenzielle Energie in Abhängigkeit von der Höhe ist
| $ V =\displaystyle\frac{1}{2} k x ^2$ |
Wenn wir die Ausdehnung als Position ausdrücken
$x = q$
ergibt sich
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
Die Gleichung kann in einer dimensionslosen Form ausgedrückt werden als
$1=y^2 + x^2$
wobei
$x=\displaystyle\frac{q}{\sqrt{2E/k}}$
ist und
$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$
wenn wir nach
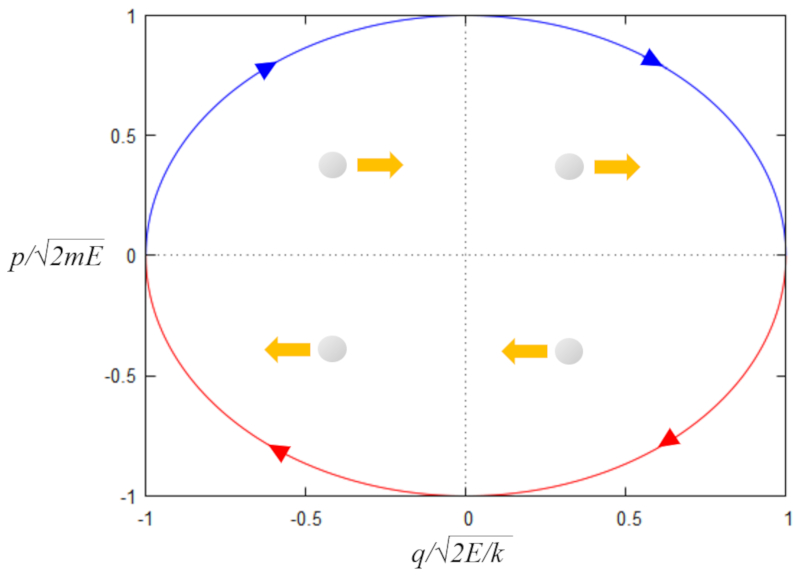
$y=\pm\sqrt{1-x^2}$
Die Darstellung in der xy-Ebene ist unten dargestellt
ID:(1187, 0)
Massen im Gravitationsfeld in Darstellung in $p-q$
Gleichung
Für den Fall einer Masse im Gravitationsfeld ist die Energie in Abhängigkeit von Impuls
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
Da die kinetische Energie
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
und die potentielle Energie
| $ V = - \displaystyle\frac{ G m M }{ r } $ |
sind, können wir die Energie in Abhängigkeit vom Radius, der durch die Variable $q$ dargestellt wird, wie folgt ausdrücken
| $ E_G = \displaystyle\frac{ p ^2}{2 m_i } - \displaystyle\frac{ G m_g M }{ q }$ |
Im Fall, dass die kinetische Energie die potentielle Energie im Anfangsradius übersteigt und die Energie positiv ist (was darauf hinweist, dass das Objekt dem Planeten entkommen kann), kann die Gleichung wie folgt geschrieben werden
$1 = \left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 - \displaystyle\frac{GmM}{Eq}$
was sich zu
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
vereinfacht, wobei
$x=\displaystyle\frac{q}{GmM/E}$
, und
$y=\displaystyle\frac{p}{2mE}$
Im Fall, dass die kinetische Energie die potentielle Energie nicht übersteigt (was darauf hinweist, dass das Objekt nicht der Anziehung des Planeten entkommen kann), ist die Energie negativ und der Ausdruck lautet
$1 = -\left(\displaystyle\frac{p}{\sqrt{2mE}}\right)^2 + \displaystyle\frac{GmM}{Eq}$
wobei $E$ der Betrag der Energie ist. Mit den Definitionen von $x$ und $y" haben wir
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
Die Gleichung kann adimensional dargestellt werden, für den Fall positiver Energie mit den folgenden Kurven (blaue und grüne Kurven):
$y=\pm\sqrt{1+\displaystyle\frac{1}{x}}$
Und für den Fall negativer Energie wird sie wie folgt dargestellt (rote und violette Kurven):
$y=\pm\sqrt{\displaystyle\frac{1}{x}-1}$
Dabei gilt
$x=\displaystyle\frac{q}{GmM/E}$
und
$y=\displaystyle\frac{p}{2mE}$
Dies wird nachfolgend dargestellt:
ID:(1185, 0)
0
Video
Video: Phasenraum