Storyboard

Bei der Feder ist die Kraft proportional zur Dehnung der Feder, so dass die Bewegungsgleichungen linear sind und die Frequenz der Schwingung von der Amplitude unabhängig ist. Dies ist der Schlüssel zur Erzeugung einer Schwingung, die nicht davon abhängt, dass die Reibung mit der Zeit abnimmt. Aus diesem Grund verwendeten alte Uhren (kreisförmige) Federn, um stabile Schwingungen zur Messung der verstrichenen Zeit zu erzeugen.

>Modell

ID:(1425, 0)

Gleichung

>Top, >Modell

Die kinetische Energie einer Masse $m$

kann in Abhängigkeit vom Impuls ausgedrückt werden als

$ K =\displaystyle\frac{ p ^2}{2 m_i }$

Bedingungen

Variablen

$p$

Moment

$kg m/s$

$K$

Raum-Zeit-Position

$J$

$m_i$

Träge Masse

$kg$

Beziehung

Entwicklung

Da die kinetische Energie gleich ist

$ K_t =\displaystyle\frac{1}{2} m_i v ^2$

und der Impuls

$ p = m_i v $

können wir es ausdrücken als

$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$

oder

$ K =\displaystyle\frac{ p ^2}{2 m_i }$

ID:(4425, 0)

Gleichung

>Top, >Modell

En el caso elástico (resorte) la fuerza es



la energía

se puede mostrar que en este caso es

$ V =\displaystyle\frac{1}{2} k x ^2$

Bedingungen

Variablen

$k$

Hookes Konstante

$N/m$

$V$

Potenzielle Energie

$J$

$x$

Verlängerung der Feder

$m$

Beziehung

Entwicklung

En el caso elástico (resorte) la fuerza es



con k la constante del resorte y x la elongación/compresión del resorte. La variación de la energía potencial es

$ \Delta W = \vec{F} \cdot \Delta\vec{s} $

\\n\\nLa diferencia\\n\\n

$\Delta x = x_2 - x_1$

\\n\\ncorresponde al camino recorrido por lo que\\n\\n

$\Delta W=k,x,\Delta x=k(x_2-x_1)\displaystyle\frac{(x_1+x_2)}{2}=\displaystyle\frac{k}{2}(x_2^2-x_1^2)$

y con ello la energía potencial elástica es

$ V =\displaystyle\frac{1}{2} k x ^2$

ID:(3246, 0)

Gleichung

>Top, >Modell

Für den Fall einer Masse, die mit einem Feder schwingt, ist die Energie als Funktion des Impulses $p$ und der Position $q$

$ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$

Bedingungen

Variablen

$E_k$

Energie eines Federsystems

$J$

$k$

Hookes Konstante

$N/m$

$p$

Moment

$kg m/s$

$s$

Posición (Vektor)

$m$

$m_i$

Träge Masse

$kg$

Beziehung

Entwicklung

Die kinetische Energie in Abhängigkeit vom Impuls ist gegeben durch

$ K =\displaystyle\frac{ p ^2}{2 m_i }$

und die potenzielle Energie in Abhängigkeit von der Höhe ist

$ V =\displaystyle\frac{1}{2} k x ^2$

Wenn wir die Ausdehnung als Position ausdrücken

$x = q$

ergibt sich

$ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$

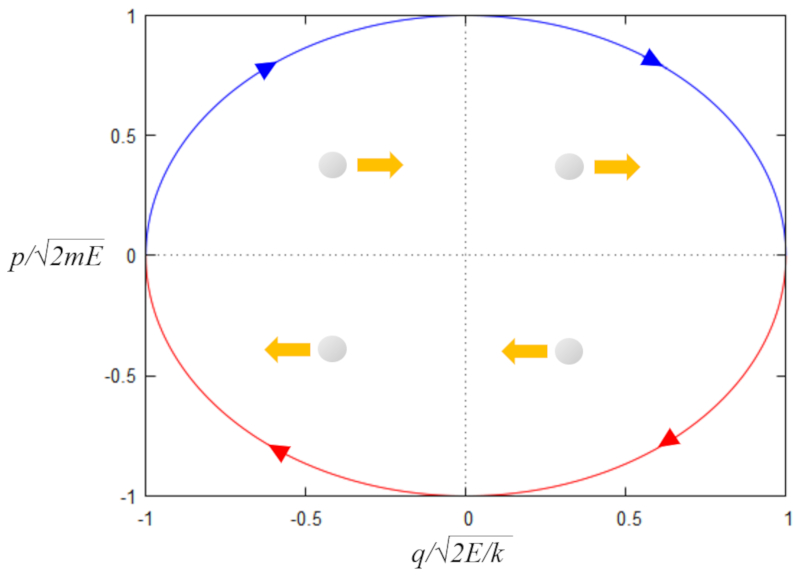
Die Gleichung kann in einer dimensionslosen Form ausgedrückt werden als

$1=y^2 + x^2$

wobei

$x=\displaystyle\frac{q}{\sqrt{2E/k}}$

ist und

$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$

wenn wir nach y auflösen, erhalten wir

$y=\pm\sqrt{1-x^2}$

Die Darstellung in der xy-Ebene ist unten dargestellt

ID:(1187, 0)

Gleichung

>Top, >Modell

Como la oscilación cumple las leyes físicas se puede hacer uso del hecho que el area debajo de la curva velocidad vs tiempo el camino recorrido para determinar el perido. Como la velocidad es\\n\\n

$\displaystyle\int_0^{T/2}v(t)dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\int_0^{T/2}\cos \displaystyle\frac{2\pi t}{T}dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\frac{T}{\pi}$

\\n\\ny el camino entre un mínimo a un máximo de una elongación, lo que ocurre entre el tiempo 0 y T/2 es igual a\\n\\n

$x_{max}-x_{min}=2\sqrt{\displaystyle\frac{2E}{k}}$

se tiene que

$ T =2 \pi \sqrt{\displaystyle\frac{ m_i }{ k }}$

Bedingungen

Variablen

$k$

Hookes Konstante

$N/m$

$\pi$

Pi

3.1415927

$rad$

$m_i$

Träge Masse

$kg$

$T$

Zeit

$s$

Beziehung

ID:(7106, 0)

Gleichung

>Top, >Modell

Eines der dargestellten Systeme ist das eines Federpendels. Dieses ist mit der elastischen Verformung des Materials verbunden, aus dem die Feder besteht. Wenn wir von "elastischer Verformung" sprechen, meinen wir eine Verformung, die nach Entfernen der aufgebrachten Spannung das System ermöglicht, seine ursprüngliche Form vollständig wiederzuerlangen. Dabei gehen wir davon aus, dass keine plastische Verformung auftritt.

Da die Energie des Federpendels gegeben ist durch

$E=\displaystyle\frac{1}{2}m_i v^2+\displaystyle\frac{1}{2}k x^2$

wird die Schwingungsdauer gleich sein zu

$T=2\pi\sqrt{\displaystyle\frac{m_i}{k}}$

und somit ist die Winkelgeschwindigkeit

$ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$

Bedingungen

Variablen

$\omega_0$

Frecuencia angular del resorte

$rad/s$

$k$

Hookes Konstante

$N/m$

$m_i$

Träge Masse

$kg$

Beziehung

Entwicklung

Da die kinetische Energie von der Masse $m$ und der Geschwindigkeit $v$ abhängt, ergibt sich

$ K_t =\displaystyle\frac{1}{2} m_i v ^2$

und die potenzielle Energie der Feder, die von der Federkonstanten $k$ und der Dehnung $x$ abhängt, ist

$ V =\displaystyle\frac{1}{2} k x ^2$

Daher wird die Gesamtenergie ausgedrückt als

$E=\displaystyle\frac{1}{2}m_i v^2+\displaystyle\frac{1}{2}k x^2$

Da die Periode ist

$T=2\pi\sqrt{\displaystyle\frac{m_i}{k}}$

können wir die Winkelgeschwindigkeit berechnen als

$\omega_0=\displaystyle\frac{2\pi}{T}=\sqrt{\displaystyle\frac{k}{m_i}}$

was bedeutet, dass

$ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$

ID:(1242, 0)

0

Video

Video: Oszillatoren auf einer Feder