Utilizador:
Lei de Darcy
Storyboard 
A lei de Hagen-Poiseuille para o fluxo total pode ser reescrita em termos de uma diferença de pressão, a taxa de fluxo e um fator que pode ser caracterizado como resistência hidráulica, o que nos leva à conhecida lei de Darcy.
ID:(877, 0)
Lei de Darcy
Storyboard
A lei de Hagen-Poiseuille para o fluxo total pode ser reescrita em termos de uma diferença de pressão, a taxa de fluxo e um fator que pode ser caracterizado como resistência hidráulica, o que nos leva à conhecida lei de Darcy.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Se considerarmos o perfil de ERROR:5449,0 para um fluido em um canal cil ndrico, onde la velocidade em um raio do cilindro ($v$) varia em rela o a ERROR:10120,0 de acordo com a seguinte express o:
envolvendo o raio do tubo ($R$) e la taxa de fluxo máxima ($v_{max}$). Podemos calcular la taxa de fluxo máxima ($v_{max}$) utilizando la viscosidade ($\eta$), la diferença de pressão ($\Delta p$) e o comprimento do tubo ($\Delta L$) da seguinte forma:
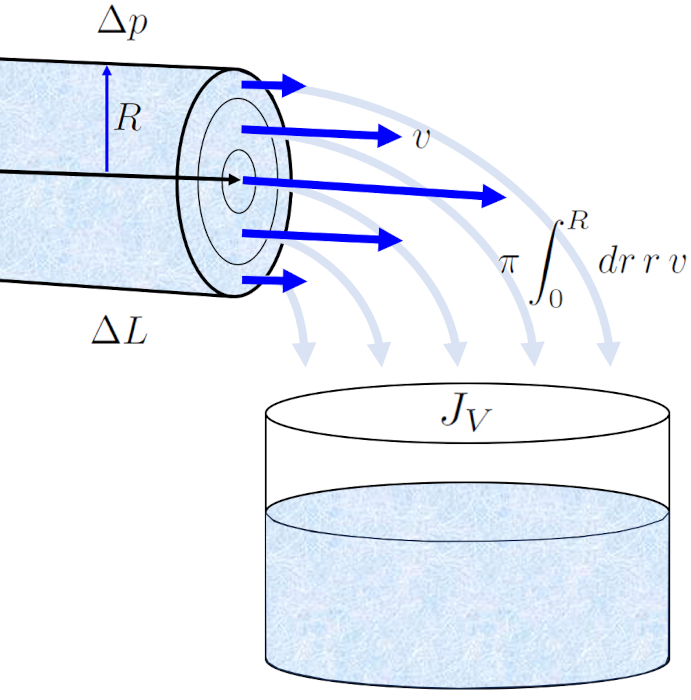
Se integrarmos a velocidade em toda a se o transversal do canal, obteremos o fluxo de volume ($J_V$), definida como a integral de $\pi r v(r)$ em rela o a ERROR:10120,0 de $0$ a ERROR:5417,0. Essa integral pode ser simplificada da seguinte maneira:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
A integra o resulta na lei de Hagen-Poiseuille resultante:
O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equa o:
Al m disso, usando a rela o para la resistência hidráulica ($R_h$):
obt m-se o resultado:
Uma vez que la resistência hidráulica ($R_h$) igual a la condutância hidráulica ($G_h$) conforme a seguinte equa o:
e uma vez que la condutância hidráulica ($G_h$) expresso em termos de la viscosidade ($\eta$), o raio do tubo ($R$) e o comprimento do tubo ($\Delta L$) da seguinte forma:
podemos concluir que:
Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):
podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:
para obter:
Exemplos
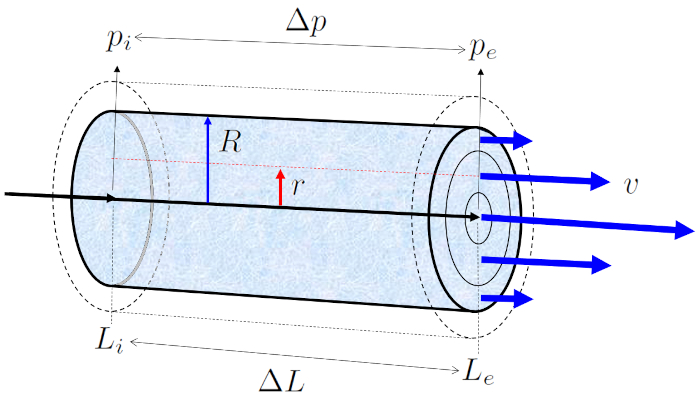
Quando um tubo preenchido com l quido de viscosidade ERROR:5422,0 exposto a la pressão na posição inicial ($p_i$) em o posição no início do tubo ($L_i$) e la pressão na posição final (e) ($p_e$) em o posição na extremidade do tubo ($L_e$), gera-se uma diferença de pressão ($\Delta p_s$) ao longo de o comprimento do tubo ($\Delta L$), resultando no perfil de la velocidade em um raio do cilindro ($v$):
Em fluxos com valores baixos de o número de Reynolds ($Re$), onde a viscosidade mais relevante do que a in rcia do l quido, o fluxo se desenvolve de forma laminar, ou seja, sem a presen a de turbul ncia.
O perfil de la velocidade em um raio do cilindro ($v$) em o raio de posição em um tubo ($r$) nos permite calcular o fluxo de volume ($J_V$) em um tubo atrav s da integra o de toda a superf cie, o que nos leva conhecida lei de Hagen-Poiseuille.
O resultado uma equa o que depende de ERROR:5417,0 elevado quarta pot ncia. No entanto, fundamental observar que este perfil de fluxo s v lido no caso de um fluxo laminar.
Assim, com isso, deduz-se de la viscosidade ($\eta$) que o fluxo de volume ($J_V$) diante de um comprimento do tubo ($\Delta L$) e ERROR:6673,1, a express o:
Os artigos originais que deram origem a esta lei com um nome combinado foram:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sobre as leis que regem o fluxo da gua em recipientes cil ndricos), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Pesquisa experimental sobre o movimento de l quidos em tubos de di metros muito pequenos), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):
podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:
para obter:
Uma vez que la resistência hidráulica ($R_h$) igual a la condutância hidráulica ($G_h$) conforme a seguinte equa o:
e uma vez que la condutância hidráulica ($G_h$) expresso em termos de la viscosidade ($\eta$), o raio do tubo ($R$) e o comprimento do tubo ($\Delta L$) da seguinte forma:
podemos concluir que:
O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equa o:
Al m disso, usando a rela o para la resistência hidráulica ($R_h$):
obt m-se o resultado:
que Henry Darcy formulou [1] para modelar o comportamento geral de meios porosos mais complexos atrav s dos quais um l quido flui.
A genialidade dessa maneira de reescrever a lei de Hagen-Poiseuille est em mostrar a analogia entre o fluxo de corrente el trica e o fluxo de l quido. Nesse sentido, a lei de Hagen-Poiseuille corresponde lei de Ohm. Isso abre a possibilidade de aplicar os conceitos de redes el tricas a sistemas de tubula es atrav s das quais um l quido flui.
Essa lei, tamb m conhecida como Lei de Darcy-Weisbach, foi publicada pela primeira vez na obra de Darcy:
[1] "Les fontaines publiques de la ville de Dijon" (As Fontes P blicas da Cidade de Dijon), Henry Darcy, Victor Dalmont Editeur, Paris (1856).
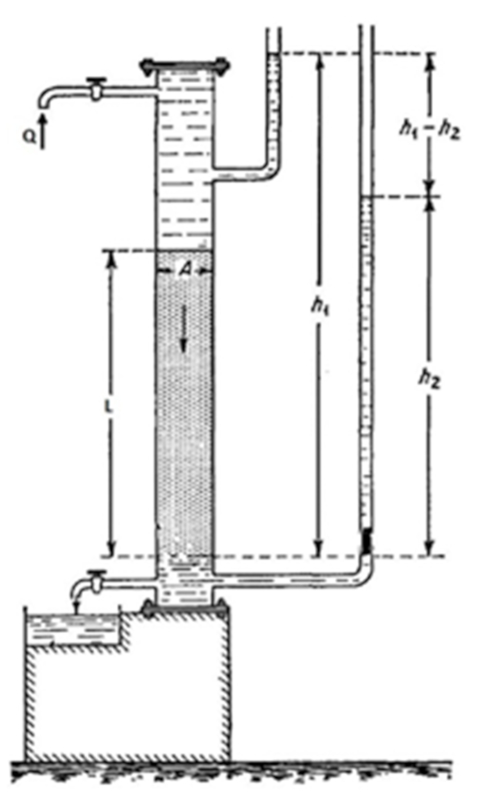
O experimento de Darcy envolve um cilindro preenchido com um material em estudo, que ent o preenchido com o l quido desejado. Na parte inferior, h uma v lvula que regula a sa da do l quido. Tanto a parte superior quanto a inferior possuem colunas de l quido associadas para determinar as press es existentes. Dessa forma, s o medidas as press es, a quantidade de l quido que flui e o tempo decorrido, o que permite determinar a resist ncia hidr ulica.
O fluxo de volume ($J_V$) pode ser calculado com a lei de Hagen-Poiseuille que com os par metros la viscosidade ($\eta$), la diferença de pressão ($\Delta p$), o raio do tubo ($R$) e o comprimento do tubo ($\Delta L$) :
Com o raio do tubo ($R$), la viscosidade ($\eta$) e o comprimento do tubo ($\Delta L$) temos que uma condutância hidráulica ($G_h$) :
Com a introdu o de la condutância hidráulica ($G_h$), podemos reescrever a equa o de Hagen-Poiseuille com la diferença de pressão ($\Delta p$) e o fluxo de volume ($J_V$) usando a seguinte equa o:
No contexto da resist ncia el trica, existe o seu inverso, conhecido como a condut ncia el trica. Da mesma forma, o que seria la condutância hidráulica ($G_h$) pode ser definido em termos de la resistência hidráulica ($R_h$) atrav s da express o:
Como la resistência hidráulica ($R_h$) igual ao inverso de la condutância hidráulica ($G_h$), ele pode ser calculado a partir da express o deste ltimo. Dessa forma, podemos identificar par metros relacionados geometria (o comprimento do tubo ($\Delta L$) e o raio do tubo ($R$)) e ao tipo de l quido (la viscosidade ($\eta$)), que podem ser denominados coletivamente como uma resistência hidráulica ($R_h$):
Darcy reescreve a equa o de Hagen Poiseuille de modo que la diferença de pressão ($\Delta p$) seja igual a la resistência hidráulica ($R_h$) vezes o fluxo de volume ($J_V$):
ID:(877, 0)
