Sustentação
Storyboard 
O fluxo ao redor de uma asa leva à formação de vórtices que, dependendo da forma e do ângulo da asa em relação ao fluxo, pode gerar vórtices em uma seção dela. Se considerarmos elementos de volume em torno da asa e assumirmos que podemos localmente assumir a conservação de energia, diferentes velocidades resultarão em diferentes pressões (Bernoulli) na superfície.
A soma de todas as pressões na superfície na direção vertical, tanto sobre a asa (força para baixo) como sob a asa (força para cima), leva a uma força total que chamamos de sustentação. Se esta força resultar positiva, podemos superar a gravidade e fazer com que o objeto (avião/ave) se eleve.
ID:(463, 0)
Sustentação
Storyboard 
O fluxo ao redor de uma asa leva à formação de vórtices que, dependendo da forma e do ângulo da asa em relação ao fluxo, pode gerar vórtices em uma seção dela. Se considerarmos elementos de volume em torno da asa e assumirmos que podemos localmente assumir a conservação de energia, diferentes velocidades resultarão em diferentes pressões (Bernoulli) na superfície. A soma de todas as pressões na superfície na direção vertical, tanto sobre a asa (força para baixo) como sob a asa (força para cima), leva a uma força total que chamamos de sustentação. Se esta força resultar positiva, podemos superar a gravidade e fazer com que o objeto (avião/ave) se eleve.
Variáveis
Cálculos
Cálculos
Equações
La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em
Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),
e para o coeficiente de elevação ($C_L$), definido como
obtemos
La força de elevação ($F_L$) junto com la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) representado por
o qual, juntamente com la massa corporal ($m$) e la aceleração gravitacional ($g$), deve ser igual a:
ou seja:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
o que resulta em:
O coeficiente de elevação ($C_L$) calculado com la massa corporal ($m$), la aceleração gravitacional ($g$), la superfície que gera sustentação ($S_w$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
Portanto, com la constante de proporcionalidade do coeficiente de sustentação ($c$) e o aceleração máxima ($\alpha$),
obtemos
La força de elevação ($F_L$) depende de la superfície que gera sustentação ($S_w$) e la diferença de pressão em um objeto ($\Delta p$) conforme
na express o para la força de elevação ($F_L$) com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$)
cont m o fator la envergadura das asas ($L$) que est associado a la superfície que gera sustentação ($S_w$). No entanto, ambos podem ser associados se considerarmos a largura da asa como a m dia de la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$). Isso nos leva a obter
La força de elevação ($F_L$) junto com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$) encontrado em
Se considerarmos la superfície que gera sustentação ($S_w$) dado por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$)
podemos reescrever a equa o para la força de elevação ($F_L$) como
$F_L =\displaystyle\frac{1}{2} \rho S_w \displaystyle\frac{4(c_bl_b-c_tl_t)}{l_b+l_t} v^2$
o que nos permite introduzir o coeficiente de sustenta o:
La força de elevação ($F_L$) est relacionado com la circulação aerodinâmica ($\Gamma$), la envergadura das asas ($L$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
Uma vez que la circulação aerodinâmica ($\Gamma$) est relacionado com o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$) da seguinte forma:
Podemos concluir que:
La circulação aerodinâmica ($\Gamma$) definido em fun o dos comprimentos la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$) juntamente com as velocidades la velocidade no topo ($v_t$) e la velocidade na parte inferior ($v_b$), da seguinte forma:
$\Gamma = -l_t v_t + l_b v_b$
Se la velocidade no topo ($v_t$) for proporcional a o fator de velocidade máxima da asa ($c_t$) em rela o a la velocidade em relação ao meio ($v$):
e la velocidade na parte inferior ($v_b$) for proporcional a o fator de velocidade inferior da asa ($c_b$) em rela o a la velocidade em relação ao meio ($v$):
podemos express -lo da seguinte forma:
$\Gamma = -l_t c_t v + l_b c_b v$
Isso nos leva seguinte equa o:
Ao relacionar la circulação aerodinâmica ($\Gamma$) com o fator de velocidade inferior da asa ($c_b$), o fator de velocidade máxima da asa ($c_t$), la comprimento inferior da asa ($l_b$) e la comprimento superior da asa ($l_t$), obtemos:
Ao estimar la superfície que gera sustentação ($S_w$) com la envergadura das asas ($L$) usando:
e calcular o coeficiente de elevação ($C_L$) com:
O resultado :
Exemplos
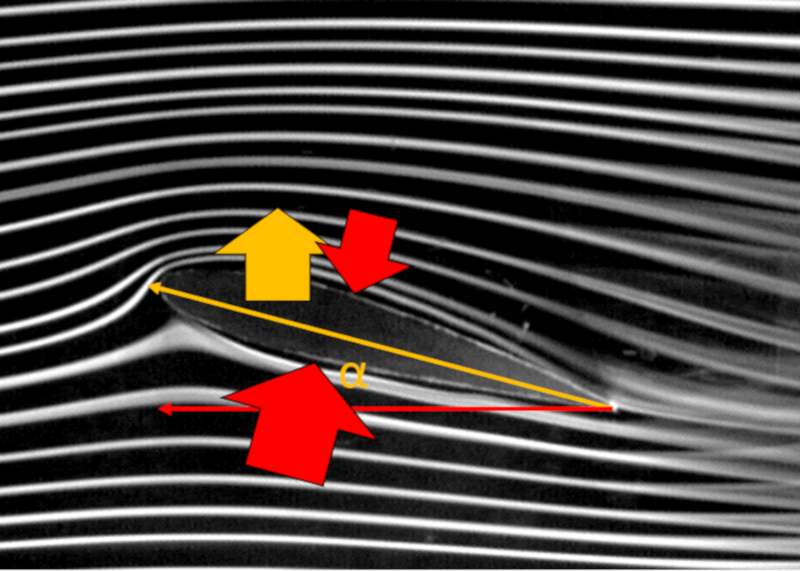
Ao observar o fluxo m dio ao redor de uma asa, pode-se notar que as linhas acima da asa s o mais longas do que as abaixo dela. Em termos simplificados, argumenta-se que devido a esse caminho mais longo, espera-se que la velocidade no topo ($v_t$) seja maior do que la velocidade na parte inferior ($v_b$), embora ambos sejam superiores a la velocidade em relação ao meio ($v$).
Se a lei de Bernoulli for aplic vel, a diferen a de velocidades resultaria em uma diferen a de press es atuando na asa. Em particular, se la velocidade no topo ($v_t$) for maior, seu correspondente la pressão no topo da asa ($p_t$) seria menor do que com la velocidade na parte inferior ($v_b$) e seu correspondente la pressão na parte inferior da asa ($p_b$). Isso implicaria na exist ncia de um la força de elevação ($F_L$) devido ao efeito dessa diferen a de press o.
No entanto, como observado em dire o ao final do perfil da asa (lado direito), a turbul ncia se forma, limitando a aplicabilidade do princ pio de Bernoulli. Especificamente, deve-se considerar que em uma certa parte do per metro da asa, a aplicabilidade pode ser limitada, e n o haver contribui o para a sustenta o.
Para definir a circula o, primeiro devemos estabelecer o caminho que ser seguido ao redor do objeto/asa no sentido contr rio ao dos ponteiros do rel gio, conforme indicado na seguinte imagem:
A circula o definida como o produto do per metro ao redor do objeto pela proje o da velocidade na superf cie. Como essa proje o de velocidade pode variar ao longo do per metro, devemos som -la atrav s de elementos infinitesimais do per metro, onde a proje o da velocidade calculada usando o produto escalar entre ela e o elemento de per metro. Graficamente, isso representado da seguinte forma:
Matematicamente, isso expresso atrav s da integral de linha fechada do produto escalar mencionado anteriormente:
Uma vez que a soma realizada no sentido contr rio ao da rota o do rel gio, na parte superior, a dire o na qual os elementos do per metro apontam oposta dire o da velocidade. Na parte inferior, ambos apontam na mesma dire o, levando a que a parte superior cancele parcialmente a parte inferior.
A associa o de la circulação aerodinâmica ($\Gamma$) com o fluxo ao redor do objeto estabelecida por meio do teorema de Kutta-Joukowski, permitindo o c lculo de la força de elevação ($F_L$) utilizando la envergadura das asas ($L$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
Simplificando a modelagem do fluxo ao redor do objeto, torna-se poss vel estimar a circula o utilizando la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$) com a seguinte equa o:
Consequentemente, la força de elevação ($F_L$) pode ser aproximado com a seguinte equa o:
Nesse contexto, o coeficiente de elevação ($C_L$) encapsula os efeitos aerodin micos do objeto.
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sobre a tarefa da teoria de asas e um novo m todo para sua deriva o), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sobre a conserva o do c rculo de ar ao redor de um perfil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
O coeficiente de sustenta o uma fun o do ngulo de ataque e geralmente segue a tend ncia indicada na figura a seguir:
No caso ilustrado, a inclina o de aproximadamente 1,5 para cada 15 graus, ou seja, 0,1 1/gra ou 5,73 1/rad.
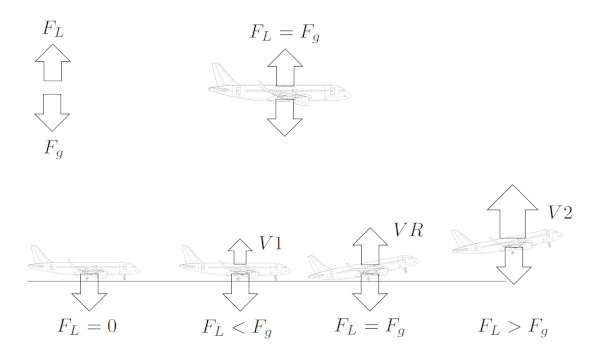
A diferen a de press o entre a parte inferior e superior da asa gera a for a de sustenta o, indicada por uma seta perpendicular superf cie da asa. Essa for a se op e for a gravitacional que atua para baixo:
As aves ou aeronaves conseguem voar quando a for a de sustenta o supera a for a gravitacional.
A diferen a de press o entre a parte inferior e superior da asa gera a for a de sustenta o, indicada por uma seta perpendicular superf cie da asa. Essa for a se op e for a gravitacional que atua para baixo:
As aves ou aeronaves conseguem voar quando a for a de sustenta o supera a for a gravitacional.
Quando um objeto est imerso em um fluxo com uma densidade de energia constante, ele divide o fluxo em um superior com la velocidade no topo ($v_t$) e um inferior com la velocidade na parte inferior ($v_b$). A velocidade est relacionada com a press o gerada, ent o tamb m existe la pressão no topo da asa ($p_t$) na parte superior e la pressão na parte inferior da asa ($p_b$) na parte inferior. Dessa forma, gerado la diferença de pressão em um objeto ($\Delta p$)
que por sua vez produz uma força de elevação ($F_L$) para contrabalan ar a for a gravitacional gerada por la massa corporal ($m$) com la aceleração gravitacional ($g$).
Se for criada uma diferen a de press o $\Delta p$ entre a parte inferior e superior de uma asa com rea $S_w$, a for a resultante ser chamada de for a de sustenta o e calculada da seguinte forma:
Essa for a de sustenta o gerada como resultado da diferen a de press o e respons vel por sustentar o voo de uma aeronave.
Com o fluxo ao redor do objeto conhecido em sua forma vetorial ao longo de toda a superf cie, poss vel calcular la circulação aerodinâmica ($\Gamma$) por meio de integra o ao longo de um caminho fechado, conforme mostrado abaixo:
No caso do fluxo que passa sobre o objeto/asa, necess rio identificar o ponto de partida e o ponto final para definir o comprimento do caminho la comprimento superior da asa ($l_t$):
Se assumirmos que la velocidade no topo ($v_t$) constante, podemos inferir a exist ncia de um fator de velocidade máxima da asa ($c_t$) de tal forma que, junto com la velocidade em relação ao meio ($v$), tenhamos:
No caso do fluxo que passa por baixo do objeto/asa, necess rio identificar o ponto de partida e o ponto final para definir o comprimento do caminho la comprimento inferior da asa ($l_b$):
Se assumirmos que la velocidade na parte inferior ($v_b$) constante, podemos inferir a exist ncia de um fator de velocidade inferior da asa ($c_b$) de tal forma que, junto com la velocidade em relação ao meio ($v$), tenhamos:
Para obter uma estimativa simplificada da circula o, podemos assumir que a velocidade constante na parte superior do per metro la velocidade no topo ($v_t$) e tamb m na parte inferior la velocidade na parte inferior ($v_b$). Se essas velocidades forem proporcionais a la velocidade em relação ao meio ($v$) com o fator de velocidade máxima da asa ($c_t$) e o fator de velocidade inferior da asa ($c_b$), e as comprimentos forem la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$), ent o la circulação aerodinâmica ($\Gamma$) calculado da seguinte maneira:
A partir dos trabalhos de Kutta [1] e Joukowski [2], foi desenvolvido um teorema que mostra a associa o entre la circulação aerodinâmica ($\Gamma$) e la força de elevação ($F_L$) atrav s de la envergadura das asas ($L$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sobre a tarefa da teoria de asas e um novo m todo para sua deriva o), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sobre a conserva o do c rculo de ar ao redor de um perfil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
La força de elevação ($F_L$) est relacionado com la circulação aerodinâmica ($\Gamma$), la envergadura das asas ($L$) com la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
Portanto, com a estimativa de la circulação aerodinâmica ($\Gamma$) em termos de o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$), temos o seguinte:
La superfície que gera sustentação ($S_w$) igual a la envergadura das asas ($L$) dividido por o largura da asa ($w$), e este ltimo pode ser estimado como a m dia de la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$), resultando em:
O coeficiente de elevação ($C_L$) pode ser calculado com base em la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$), o fator de velocidade máxima da asa ($c_t$) e o fator de velocidade inferior da asa ($c_b$) da seguinte forma:
La circulação aerodinâmica ($\Gamma$) finalmente resumido em um c lculo que envolve la superfície que gera sustentação ($S_w$), la envergadura das asas ($L$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) atrav s da equa o:
Para gerar uma press o maior abaixo do que acima da asa e gerar sustenta o, utiliza-se o princ pio de Bernoulli, corrigindo a falta de conserva o da densidade de energia com um coeficiente de elevação ($C_L$). A press o sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) atrav s da seguinte f rmula:
Para que uma nave ou uma ave possam permanecer em voo, la força gravitacional ($F_g$) deve contrariar a for a da gravidade, que definida por la massa corporal ($m$) e la aceleração gravitacional ($g$). Em outras palavras, deve ser:
Esta uma situa o simplificada que n o leva em considera o que a for a de resist ncia tamb m pode gerar uma for a de sustenta o.
A partir de medi es, conclui-se que o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$:
Ap s um certo ngulo, a curva diminui at chegar a zero. Isso ocorre porque acima desse ngulo cr tico, os redemoinhos cobrem completamente a superf cie superior da asa, levando perda de sustenta o. Esse fen meno conhecido como \"stall\" (estol em portugu s).
A condi o para atingir o voo cumprida quando la força de elevação ($F_L$) igual ao peso da aeronave ou ave, calculado a partir de la massa corporal ($m$) e la aceleração gravitacional ($g$). Isso alcan ado com valores suficientes de ERROR:6110,0, la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$), sendo este ltimo coeficiente o fator ajust vel. No caso de aeronaves, os pilotos podem modificar o valor de o coeficiente de elevação ($C_L$) usando flaps, cujo valor deve satisfazer:
Os flaps s o ajustados ao variar o ngulo que a asa faz com a dire o do voo, conhecido como ngulo de ataque.
Como o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$, podemos calcular o ngulo necess rio para alcan ar sustenta o suficiente para uma velocidade $v$ dada:
onde $m$ a massa, $g$ a acelera o gravitacional, $\rho$ a densidade do meio, $S_w$ a rea da asa e $c$ a constante de proporcionalidade entre o coeficiente de sustenta o e o ngulo de ataque.
ID:(463, 0)