Sustentación
Storyboard 
El flujo en torno a un ala lleva la formación de torbellinos que según la forma y angulo del ala con respecto del flujo puede originar torbellinos en una sección de estos. Si se consideran elementos de volumen en torno del ala y se asume que se puede locamente asumir conservación de energía se tiene que las distintas velocidades llevaran a distintas presiones (Bernoulli) sobre la superficie.
La suma de todas las presiones sobre la superficie en la dirección vertical, tanto sobre el ala (fuerza hacia abajo) como debajo del ala (fuerza hacia arriba) llevan a una fuerza total que denominamos sustentación. Si esta resulta positiva podemos lograr superar la gravedad y hacer que el cuerpo (avión/ave) se eleve.
ID:(463, 0)
Sustentación
Storyboard 
El flujo en torno a un ala lleva la formación de torbellinos que según la forma y angulo del ala con respecto del flujo puede originar torbellinos en una sección de estos. Si se consideran elementos de volumen en torno del ala y se asume que se puede locamente asumir conservación de energía se tiene que las distintas velocidades llevaran a distintas presiones (Bernoulli) sobre la superficie. La suma de todas las presiones sobre la superficie en la dirección vertical, tanto sobre el ala (fuerza hacia abajo) como debajo del ala (fuerza hacia arriba) llevan a una fuerza total que denominamos sustentación. Si esta resulta positiva podemos lograr superar la gravedad y hacer que el cuerpo (avión/ave) se eleve.
Variables
Cálculos
Cálculos
Ecuaciones
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
y para el coeficiente de sustentación ($C_L$), definido como
obtenemos
La fuerza de sustentación ($F_L$) junto con la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) se representa como
lo cual, junto con la masa del cuerpo ($m$) y la aceleración gravitacional ($g$), debe ser igual a:
es decir:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
lo que resulta en:
El coeficiente de sustentación ($C_L$) se calcula con la masa del cuerpo ($m$), la aceleración gravitacional ($g$), la superficie que genera sustentación ($S_w$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) de la siguiente manera:
As , con la constante de proporcionalidad del coeficiente de sustentación ($c$) y el angulo de ataque del ala ($\alpha$)
se obtiene
La fuerza de sustentación ($F_L$) depende de la superficie que genera sustentación ($S_w$) y la diferencia de presión sobre un objeto ($\Delta p$) seg n
en la expresi n para la fuerza de sustentación ($F_L$) con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$)
contiene el factor la envergadura de las alas ($L$) que se asocia a la superficie que genera sustentación ($S_w$). Sin embargo, ambos se pueden asociar si se considera el ancho del ala como el promedio de la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$). Esto nos lleva a obtener
La fuerza de sustentación ($F_L$) junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$) se encuentra en
Si consideramos la superficie que genera sustentación ($S_w$) dado por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$)
podemos reescribir la ecuaci n de la fuerza de sustentación ($F_L$) como
$F_L =\displaystyle\frac{1}{2} \rho S_w \displaystyle\frac{4(c_bl_b-c_tl_t)}{l_b+l_t} v^2$
lo que nos permite introducir el coeficiente de sustentaci n:
La fuerza de sustentación ($F_L$) se relaciona con la circulación aerodinamica ($\Gamma$), la envergadura de las alas ($L$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) de la siguiente manera:
Dado que la circulación aerodinamica ($\Gamma$) se relaciona con el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$) de la siguiente manera:
Podemos concluir que:
La circulación aerodinamica ($\Gamma$) se define en funci n de las longitudes la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$) junto con las velocidades la velocidad en la parte superior ($v_t$) y la velocidad en la parte inferior ($v_b$), de la siguiente manera:
$\Gamma = -l_t v_t + l_b v_b$
Si la velocidad en la parte superior ($v_t$) es proporcional a el factor de velocidad superior del ala ($c_t$) con respecto a la velocidad respecto del medio ($v$):
y la velocidad en la parte inferior ($v_b$) es proporcional a el factor de velocidad inferior del ala ($c_b$) con respecto a la velocidad respecto del medio ($v$):
podemos expresarlo como:
$\Gamma = -l_t c_t v + l_b c_b v$
Esto nos lleva a la siguiente ecuaci n:
Al relacionar la circulación aerodinamica ($\Gamma$) con el factor de velocidad inferior del ala ($c_b$), el factor de velocidad superior del ala ($c_t$), la largo inferior del ala ($l_b$) y la largo superior del ala ($l_t$), obtenemos:
Mediante la estimaci n de la superficie que genera sustentación ($S_w$) con la envergadura de las alas ($L$) utilizando:
y calculando el coeficiente de sustentación ($C_L$) con:
Obtenemos como resultado:
Ejemplos
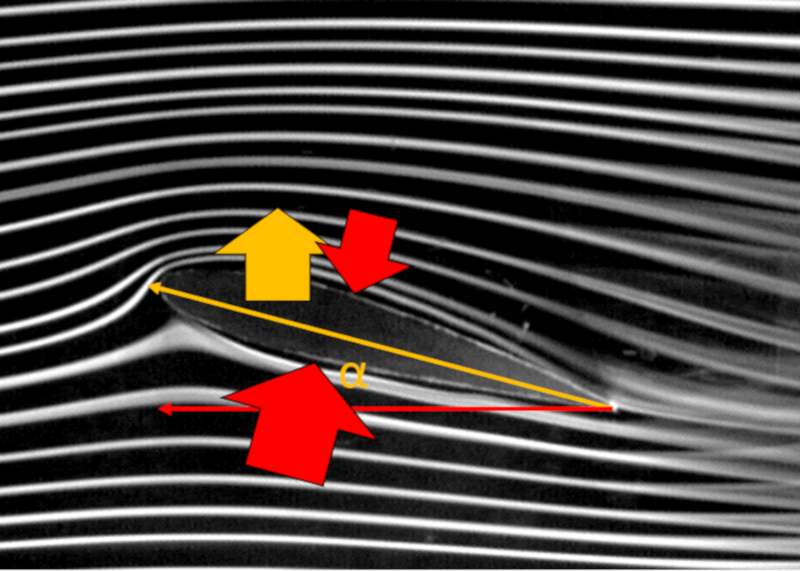
Al observar el flujo promedio alrededor de un ala, se puede notar que las l neas sobre el ala son m s largas que las del lado inferior. En t rminos simplificados, se argumenta que debido a esta trayectoria m s larga, se espera que la velocidad en la parte superior ($v_t$) sea mayor que la velocidad en la parte inferior ($v_b$), aunque ambos sean superiores a la velocidad respecto del medio ($v$).
Si la ley de Bernoulli es aplicable, la diferencia de velocidades resultar a en una diferencia de presiones que act an sobre el ala. En particular, si la velocidad en la parte superior ($v_t$) es mayor, su correspondiente la presión en la parte superior del ala ($p_t$) ser a menor que con la velocidad en la parte inferior ($v_b$) y su correspondiente la presión en la parte Inferior del ala ($p_b$). Esto implicar a la existencia de una la fuerza de sustentación ($F_L$) debido al efecto de esta diferencia de presi n.
Sin embargo, como se ve hacia el final del perfil del ala (lado derecho), se forman turbulencias, lo que limita la aplicabilidad del principio de Bernoulli. Espec ficamente, se debe considerar que en una cierta parte del per metro del ala, puede que no sea aplicable y no contribuir a la sustentaci n.
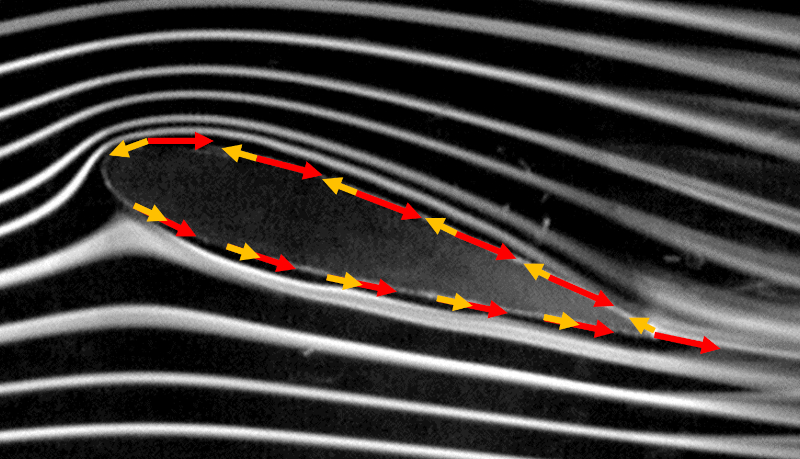
Para definir la circulaci n, primero debemos establecer la trayectoria que se seguir alrededor del objeto/ala en un sentido contrario al de las agujas del reloj, como se indica en la siguiente imagen:
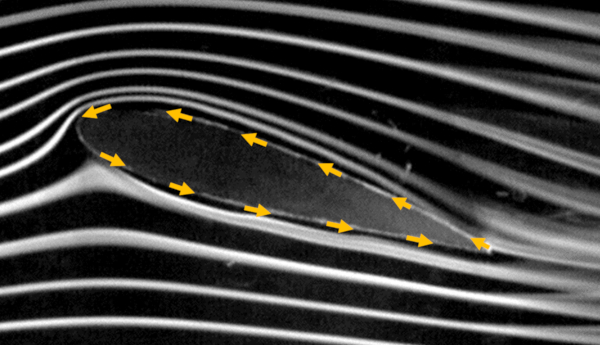
La circulaci n se define como el producto del per metro alrededor del objeto por la proyecci n de la velocidad sobre la superficie. Dado que esta proyecci n de la velocidad puede variar a lo largo del per metro, debemos sumarla a trav s de elementos infinitesimales del per metro, donde la proyecci n de la velocidad se calcula mediante el producto escalar entre esta y el elemento del per metro. Gr ficamente, esto se representa de la siguiente manera:
Matem ticamente, esto se expresa mediante la integral de l nea cerrada del producto escalar mencionado anteriormente:
Dado que la suma se realiza en sentido contrario a la rotaci n del reloj, en la parte superior, la direcci n en la que apuntan los elementos del per metro es opuesta a la direcci n de la velocidad. En la parte inferior, ambos apuntan en la misma direcci n, por lo que la suma lleva a que la parte superior en parte anule a la inferior.
La asociaci n de la circulación aerodinamica ($\Gamma$) con el flujo alrededor del objeto se logra mediante el teorema de Kutta-Joukowski, lo que permite calcular la fuerza de sustentación ($F_L$) con la envergadura de las alas ($L$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) utilizando la ecuaci n:
Al simplificar el modelado del flujo alrededor del objeto, se vuelve posible estimar la circulaci n con la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$) utilizando la ecuaci n:
De esta manera, la fuerza de sustentación ($F_L$) puede ser estimado con la ecuaci n:
Donde el coeficiente de sustentación ($C_L$) resume el efecto aerodin mico del objeto.
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sobre la tarea de la teor a de alas y un nuevo m todo para su derivaci n.), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sobre la conservaci n del c rculo de aire alrededor de un perfil.), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
El coeficiente de sustentación ($C_L$) es una funci n del ERROR:6121,0 y generalmente sigue la tendencia indicada en la siguiente figura:
En el caso representado, la pendiente es del orden de 1.5 por cada 15 grados, es decir, 0.1 1/grado o 5.73 1/radian.
La diferencia de presi n entre la parte inferior y superior del ala genera la fuerza de sustentación ($F_L$), representada por una flecha perpendicular a la superficie del ala. A esta fuerza se le opone la fuerza gravitacional ($F_g$) que act a hacia abajo:
Para maximizar la fuerza de sustentación ($F_L$) existen cuatro factores para considerar:
• la velocidad respecto del medio ($v$) que alcanza el avi n o ave seg n la propulsi n que tiene, la resistencia aeodinamica que sufre y el largo de la mista que dispone
• la constante de proporcionalidad del coeficiente de sustentación ($c$) que define el dise o del ala y que logra sustentaci n via la rotaci n del avi n
• el angulo de ataque del ala ($\alpha$) que se controlan mediante los flaps que estan en la parte posterior de las alas y que se extienden o contraen
• la superficie que genera sustentación ($S_w$) que se define con el dise o
La ecuaci n para el el angulo de ataque del ala ($\alpha$) que depende de la masa del cuerpo ($m$), la aceleración gravitacional ($g$), la constante de proporcionalidad del coeficiente de sustentación ($c$), la superficie que genera sustentación ($S_w$), la densidad ($\rho$) y la velocidad respecto del medio ($v$)
esta en el centro del proceso de un despegue despegue. En particula indica los limites para
• el tipo de avi n (la superficie que genera sustentación ($S_w$))
• la masa del cuerpo ($m$) con que pretende despegar,
• el angulo de ataque del ala ($\alpha$) definido por la posici n de los flaps
• la velocidad respecto del medio ($v$) que se debe haber alcanzado
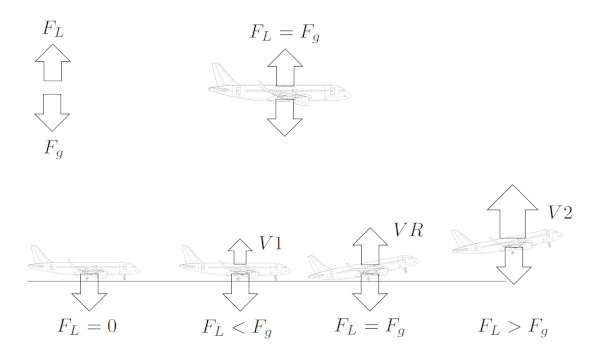
El proceso de despegue tiene cuatro puntos claves repreentados en la siguiente grafica:
El proceso de despegue se inicia en el extremo de la pista en que el avi n no tiene velocidad y por ello se experimenta la fuerza de sustentación ($F_L$).
Dentro del proceso se alcanza la velocidad $V1$ (Takeoff Decision Speed) en que el avi n aun no esta en condiciones de despegar (la fuerza de sustentación ($F_L$) es aun menor que la fuerza gravitacional ($F_g$)) pero es el momento en que si deside abortar el despegue tiene un largo de pista para lograr detenerse. Pasado este punto el avi n, incluso con un problema t cnico, tiene que necesariamente despegar pudiendo volver a aterrizar de emergencia.
En el proxiumo paso se alcanza la velocida de rotaci n $VR$ (Rotation Speed) que es la velocidad en que el avi n puede iniciar la rotaci n que agrandara el angulo de ataque del ala ($\alpha$) de ataque con lo aue se incrementa el coeficiente de sustentación ($C_L$) generando suficiente la fuerza de sustentación ($F_L$) para lograr despegar o sea que supere la fuerza gravitacional ($F_g$).
Finalmente se alcanza la velocidad $V2$ (Takeoff Safety Speed) en que la velocidad es sufiente para continuar el despegue incluso si uno de los motores fallara. En este punto el coeficiente de sustentación ($C_L$) supera la fuerza gravitacional ($F_g$) y el avi n se eleva.
A medida que el avi n se eleva la la velocidad respecto del medio ($v$) se continua incrementando llegando a la velocidad de crucero. El aumento de la velocidad respecto del medio ($v$) es compensado con una reducci n de el angulo de ataque del ala ($\alpha$) que se logra retrayendo los flags en las alas.
Cuando un objeto se encuentra inmerso en un flujo con una densidad de energ a constante, este divide el flujo en uno superior con la velocidad en la parte superior ($v_t$) y uno inferior con la velocidad en la parte inferior ($v_b$). La velocidad se relaciona con la presi n que se genera, por lo que tambi n se tiene en la parte superior la presión en la parte superior del ala ($p_t$) e inferior con la presión en la parte Inferior del ala ($p_b$). De esta forma, se genera la diferencia de presión sobre un objeto ($\Delta p$)
que a su vez produce una fuerza de sustentación ($F_L$) para contrarrestar la fuerza gravitacional generada por la masa del cuerpo ($m$) con la aceleración gravitacional ($g$).
Si se logra crear una diferencia de la diferencia de presión sobre un objeto ($\Delta p$) entre la parte inferior y superior de un ala con la superficie que genera sustentación ($S_w$), la fuerza resultante se denomina la fuerza de sustentación ($F_L$) y se calcula de la siguiente manera:
Esta fuerza de sustentaci n es generada como resultado de la diferencia de presi n y es la responsable de sostener el vuelo de una aeronave.
Con el flujo alrededor del objeto conocido en su forma vectorial a lo largo de toda la superficie, es posible calcular la circulación aerodinamica ($\Gamma$) mediante la integraci n a lo largo de un camino cerrado, como se muestra a continuaci n:
Esta formulaci n asume que el cuerpo es infinitamente extenso en la direcci n perpendicular al campo de flujo.
En el caso del flujo que pasa por encima del objeto/ala, es necesario identificar el punto de inicio y el punto final para definir la longitud del camino la largo superior del ala ($l_t$):
Si suponemos que la velocidad en la parte superior ($v_t$) es constante, podemos inferir la existencia de un factor de velocidad superior del ala ($c_t$) tal que, junto con la velocidad respecto del medio ($v$), se tenga:
En el caso del flujo que pasa por debajo del objeto/ala debe identificarse el punto de inicio de la linea y el final con lo que se define el camino de unlargo la largo inferior del ala ($l_b$):
Si suponemos que la velocidad en la parte inferior ($v_b$) es constante, podemos inferir la existencia de un factor de velocidad inferior del ala ($c_b$) tal que, junto con la velocidad respecto del medio ($v$), se tenga:
Para obtener una estimaci n simplificada de la circulaci n, podemos asumir que la velocidad es constante en la parte superior del per metro la velocidad en la parte superior ($v_t$) y tambi n en la parte inferior la velocidad en la parte inferior ($v_b$). Si estas velocidades son proporcionales a la velocidad respecto del medio ($v$) con el factor de velocidad superior del ala ($c_t$) y el factor de velocidad inferior del ala ($c_b$), y las longitudes son la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$), entonces la circulación aerodinamica ($\Gamma$) se calcula de la siguiente manera:
De los trabajos de Kutta [1] y Joukowski [2] se deriv un teorema que establece una relaci n entre la circulación aerodinamica ($\Gamma$) y la fuerza de sustentación ($F_L$) a trav s de la envergadura de las alas ($L$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sobre la tarea de la teor a de alas y un nuevo m todo para su derivaci n.), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sobre la conservaci n del c rculo de aire alrededor de un perfil.), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
La fuerza de sustentación ($F_L$) se relaciona con la circulación aerodinamica ($\Gamma$), la envergadura de las alas ($L$) con la densidad ($\rho$) y la velocidad respecto del medio ($v$) de la siguiente manera:
Por lo tanto, con la estimaci n de la circulación aerodinamica ($\Gamma$) en funci n de el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$), obtenemos lo siguiente:
La superficie que genera sustentación ($S_w$) es igual a la envergadura de las alas ($L$) dividido por el ancho del ala ($w$), y este ltimo se puede estimar como el promedio de la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$), por lo que obtenemos:
El coeficiente de sustentación ($C_L$) se puede calcular en funci n de la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$), el factor de velocidad superior del ala ($c_t$) y el factor de velocidad inferior del ala ($c_b$) de la siguiente manera:
La circulación aerodinamica ($\Gamma$) se resume finalmente en un c lculo que involucra la superficie que genera sustentación ($S_w$), la envergadura de las alas ($L$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) a trav s de la ecuaci n:
Para crear una presi n mayor debajo que encima del ala y generar sustentaci n, se emplea la Ley de Bernoulli, corrigiendo la falta de conservaci n de la densidad de energ a mediante un coeficiente de sustentación ($C_L$). La presi n sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
Para que una nave o un ave puedan mantenerse en vuelo, la fuerza gravitacional ($F_g$) tiene que contrarrestar la fuerza de gravedad, que est definida por la masa del cuerpo ($m$) y la aceleración gravitacional ($g$). En otras palabras tiene que ser:
Esta es una situaci n simplificada en que no se considera que la fuerza de resistencia tambien puede generar una fuerza de sustentaci n.
A partir de mediciones, se concluye que el coeficiente de sustentación ($C_L$) es proporcional al ERROR:6121,0 siendo la constante de proporcionalidad del coeficiente de sustentación ($c$):
Despu s de cierto ngulo, la curva disminuye hasta llegar a cero. Esto se debe a que sobre dicho ngulo cr tico, los v rtices cubren completamente la superficie superior del ala, lo que resulta en la p rdida de sustentaci n. Este fen meno se conoce como "stall" (entrada en p rdida).
La condici n para lograr el vuelo se cumple cuando la fuerza de sustentación ($F_L$) es igual al peso de la aeronave o ave, calculado a partir de la masa del cuerpo ($m$) y la aceleración gravitacional ($g$). Esto se consigue con suficientes valores adecuados de ERROR:6110,0, la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$), donde este ltimo coeficiente es el factor que se puede ajustar. En el caso de las aeronaves, el piloto puede modificar el valor de el coeficiente de sustentación ($C_L$) utilizando los llamados flaps, cuyo valor debe cumplir con:
Los flaps se ajustan al variar el ngulo que el ala forma con la direcci n de vuelo, conocido como ngulo de ataque.
Como el coeficiente de sustentación ($C_L$) es proprocional al el angulo de ataque del ala ($\alpha$), donde el factor de proprocionalidad es la constante de proporcionalidad del coeficiente de sustentación ($c$) se puede calcular el angulo necesario para volar con la masa del cuerpo ($m$), la aceleración gravitacional ($g$), la superficie que genera sustentación ($S_w$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) mediante:
Es importante considerar que la lienalidad esta limitada a un angulo menor que unos 35 a 40 sobre el cual colapsa en forma catastrofica la sustentaci n. Por ello el angulo de ataque nunca se elige mayor a 30 o en la gerga de la aviaci n flap 30.
ID:(463, 0)