Auftrieb
Storyboard 
Die Umströmung eines Flügels führt zur Bildung von Strudeln, die je nach Form und Winkel des Flügels in Bezug auf die Strömung in einem Abschnitt davon Strudel verursachen können. Wenn Volumenelemente um den Flügel herum betrachtet werden und angenommen wird, dass Energieeinsparung toll angenommen werden kann, haben die unterschiedlichen Geschwindigkeiten unterschiedliche Drücke (Bernoulli) auf der Oberfläche.
Die Summe aller Drücke auf die Oberfläche in vertikaler Richtung, sowohl auf den Flügel (Abwärtskraft) als auch unter den Flügel (Aufwärtskraft), führt zu einer Gesamtkraft, die wir Auftrieb nennen. Wenn dies positiv ist, können wir die Schwerkraft überwinden und den Körper (Flugzeug / Vogel) aufstehen lassen.
ID:(463, 0)
Auftrieb
Storyboard 
Die Umströmung eines Flügels führt zur Bildung von Strudeln, die je nach Form und Winkel des Flügels in Bezug auf die Strömung in einem Abschnitt davon Strudel verursachen können. Wenn Volumenelemente um den Flügel herum betrachtet werden und angenommen wird, dass Energieeinsparung toll angenommen werden kann, haben die unterschiedlichen Geschwindigkeiten unterschiedliche Drücke (Bernoulli) auf der Oberfläche. Die Summe aller Drücke auf die Oberfläche in vertikaler Richtung, sowohl auf den Flügel (Abwärtskraft) als auch unter den Flügel (Aufwärtskraft), führt zu einer Gesamtkraft, die wir Auftrieb nennen. Wenn dies positiv ist, können wir die Schwerkraft überwinden und den Körper (Flugzeug / Vogel) aufstehen lassen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
und f r der Koeffizient Fahrstuhl ($C_L$), definiert als
erhalten wir
Die Auftriebskraft ($F_L$) zusammen mit die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wird durch
repr sentiert, was zusammen mit die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) gleich sein muss:
das hei t:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
daraus ergibt sich:
Der Koeffizient Fahrstuhl ($C_L$) wird wie folgt mit die Körpermasse ($m$), die Gravitationsbeschleunigung ($g$), die Oberfläche, die Auftrieb erzeugt ($S_w$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) berechnet:
Daher, mit die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$) und der Anstellwinkel eines Flügels ($\alpha$),
erhalten wir
Die Auftriebskraft ($F_L$) h ngt von die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Druckdifferenz auf einem Objekt ($\Delta p$) ab gem
in der Ausdrucksweise f r die Auftriebskraft ($F_L$) mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$)
enth lt den Faktor die Spannweite der Flügel ($L$), der mit die Oberfläche, die Auftrieb erzeugt ($S_w$) in Verbindung steht. Beide k nnen jedoch in Verbindung gebracht werden, wenn wir die Fl gelbreite als Durchschnitt von die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) betrachten. Dies f hrt uns zu erhalten
Die Auftriebskraft ($F_L$) zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$) findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) unter Ber cksichtigung von die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) betrachten
k nnen wir die Gleichung f r die Auftriebskraft ($F_L$) umschreiben als
$F_L =\displaystyle\frac{1}{2} \rho S_w \displaystyle\frac{4(c_bl_b-c_tl_t)}{l_b+l_t} v^2$
was es uns erm glicht, den Auftriebsbeiwert einzuf hren:
Die Auftriebskraft ($F_L$) steht in Beziehung zu die Aerodynamische Zirkulation ($\Gamma$), die Spannweite der Flügel ($L$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wie folgt:
Da die Aerodynamische Zirkulation ($\Gamma$) in Beziehung zu der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) wie folgt steht:
K nnen wir folgern:
Die Aerodynamische Zirkulation ($\Gamma$) wird in Abh ngigkeit von den L ngen die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) sowie den Geschwindigkeiten die Geschwindigkeit an der Oberseite ($v_t$) und die Geschwindigkeit an der Unterseite ($v_b$) wie folgt definiert:
$\Gamma = -l_t v_t + l_b v_b$
Wenn die Geschwindigkeit an der Oberseite ($v_t$) proportional zu der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$) in Bezug auf die Geschwindigkeit in Bezug auf das Medium ($v$) ist:
und die Geschwindigkeit an der Unterseite ($v_b$) proportional zu der Flügelbodengeschwindigkeitsfaktor ($c_b$) in Bezug auf die Geschwindigkeit in Bezug auf das Medium ($v$) ist:
k nnen wir es wie folgt ausdr cken:
$\Gamma = -l_t c_t v + l_b c_b v$
Dies f hrt uns zu folgender Gleichung:
Wenn wir die Aerodynamische Zirkulation ($\Gamma$) in Beziehung zu der Flügelbodengeschwindigkeitsfaktor ($c_b$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), die Länge des unteren Flügels ($l_b$) und die Obere Flügellänge ($l_t$) setzen, ergibt sich:
Durch die Sch tzung von die Oberfläche, die Auftrieb erzeugt ($S_w$) mit die Spannweite der Flügel ($L$) mittels:
und die Berechnung von der Koeffizient Fahrstuhl ($C_L$) mit:
ergibt sich:
Beispiele
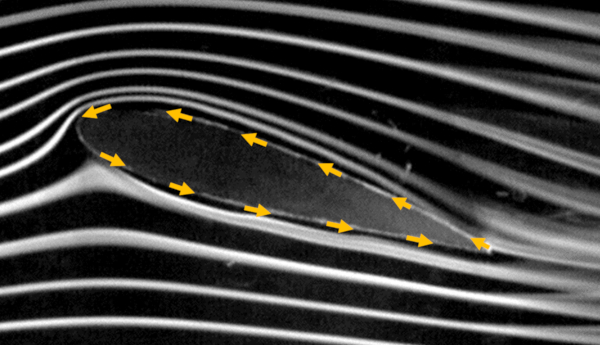
Beim Betrachten des durchschnittlichen Str mungsverhaltens um einen Fl gel f llt auf, dass die Linien ber dem Fl gel l nger sind als die unterhalb. In vereinfachten Begriffen wird argumentiert, dass aufgrund dieses l ngeren Wegs erwartet wird, dass die Geschwindigkeit an der Oberseite ($v_t$) gr er ist als die Geschwindigkeit an der Unterseite ($v_b$), obwohl beide h her sind als die Geschwindigkeit in Bezug auf das Medium ($v$).
Wenn das Bernoulli-Gesetz anwendbar ist, w rde die Geschwindigkeitsdifferenz zu einem Druckunterschied f hren, der auf den Fl gel wirkt. Insbesondere, wenn die Geschwindigkeit an der Oberseite ($v_t$) gr er ist, w re das zugeh rige die Druck auf der Oberseite des Flügels ($p_t$) niedriger als bei die Geschwindigkeit an der Unterseite ($v_b$) und das zugeh rige die Druck auf die Unterseite des Flügels ($p_b$). Dies w rde auf das Vorhandensein eines die Auftriebskraft ($F_L$) aufgrund dieses Druckunterschieds hinweisen.
Jedoch bildet sich gegen Ende des Profils des Fl gels (rechte Seite) Turbulenz, was die Anwendbarkeit des Bernoulli-Prinzips einschr nkt. Es sollte insbesondere ber cksichtigt werden, dass in einem bestimmten Teil des Umfangs des Fl gels die Anwendbarkeit nicht gegeben sein kann und somit keine Beitrag zur Auftrieb leistet.
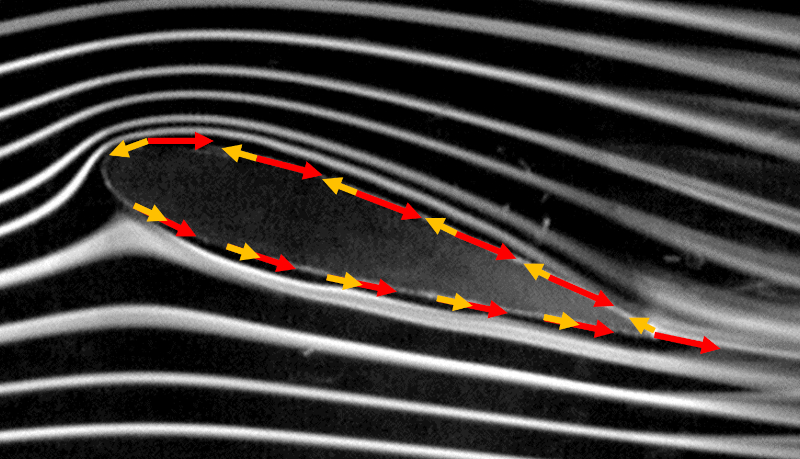
Um die Zirkulation zu definieren, m ssen wir zun chst den Pfad festlegen, der um das Objekt/den Fl gel in entgegen dem Uhrzeigersinn verfolgt wird, wie in der folgenden Abbildung dargestellt:
Die Zirkulation wird als das Produkt des Umfangs um das Objekt und der Projektion der Geschwindigkeit auf die Oberfl che definiert. Da diese Geschwindigkeitsprojektion entlang des Umfangs variieren kann, m ssen wir sie ber infinitesimale Elemente des Umfangs summieren, wobei die Geschwindigkeitsprojektion mithilfe des Skalarprodukts zwischen ihr und dem Umfeldelement berechnet wird. Grafisch wird dies wie folgt dargestellt:
Mathematisch wird dies durch das geschlossene Linienintegral des oben genannten Skalarprodukts ausgedr ckt:
Da die Summe gegen den Uhrzeigersinn erfolgt, zeigt in der oberen H lfte die Richtung, in die die Umfeldelemente zeigen, entgegengesetzt zur Richtung der Geschwindigkeit. In der unteren H lfte zeigen beide in die gleiche Richtung, wodurch die obere H lfte teilweise die untere H lfte aufhebt.
Die Beziehung zwischen die Aerodynamische Zirkulation ($\Gamma$) und dem um das Objekt flie enden Strom wird durch den Kutta-Joukowski-Satz hergestellt, was die Berechnung von die Auftriebskraft ($F_L$) unter Verwendung von die Spannweite der Flügel ($L$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wie folgt erm glicht:
Durch Vereinfachung der Modellierung des Str mungsverhaltens um das Objekt herum wird es m glich, die Zirkulation mithilfe von die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$) mit der folgenden Gleichung zu sch tzen:
Folglich kann die Auftriebskraft ($F_L$) mit der folgenden Gleichung approximiert werden:
Hierbei ber cksichtigt der Koeffizient Fahrstuhl ($C_L$) die aerodynamischen Effekte des Objekts.
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben.", Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." , Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
Der Auftriebsbeiwert ist eine Funktion des Anstellwinkels und folgt in der Regel dem in der folgenden Abbildung dargestellten Trend:
Im gezeigten Fall betr gt die Steigung ungef hr 1,5 pro 15 Grad, was 0,1 1/Grad oder 5,73 1/Radiant entspricht.
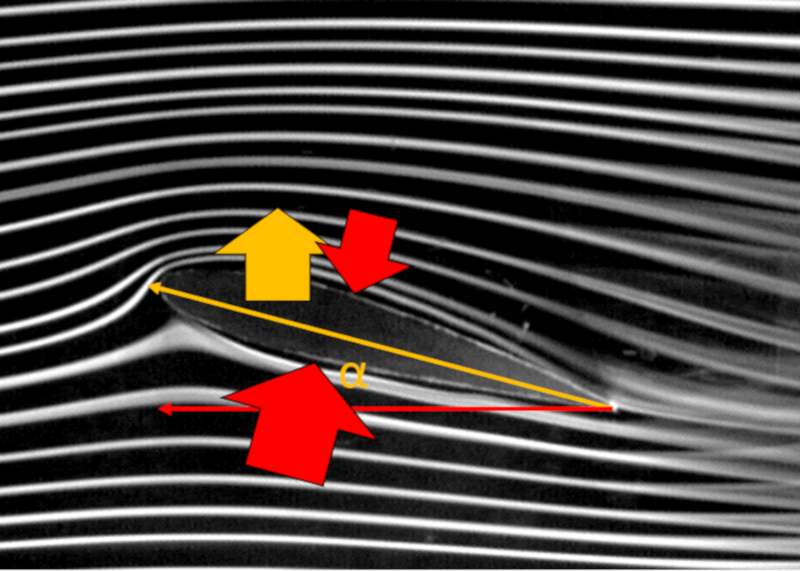
Der Druckunterschied zwischen der Unter- und Oberseite des Fl gels erzeugt die Auftriebskraft, die durch einen Pfeil senkrecht zur Fl geloberfl che dargestellt wird. Dieser Kraft wirkt die Schwerkraft entgegen, die nach unten gerichtet ist:
V gel oder Flugzeuge k nnen fliegen, wenn die Auftriebskraft die Schwerkraft bersteigt.
Der Druckunterschied zwischen der Unter- und Oberseite des Fl gels erzeugt die Auftriebskraft, die durch einen Pfeil senkrecht zur Fl geloberfl che dargestellt wird. Dieser Kraft wirkt die Schwerkraft entgegen, die nach unten gerichtet ist:
V gel oder Flugzeuge k nnen fliegen, wenn die Auftriebskraft die Schwerkraft bersteigt.
Wenn ein Objekt in einem Strom mit konstanter Energiedichte eingetaucht ist, teilt es den Strom in einen oberen mit die Geschwindigkeit an der Oberseite ($v_t$) und einen unteren mit die Geschwindigkeit an der Unterseite ($v_b$). Die Geschwindigkeit ist mit dem erzeugten Druck verbunden, daher gibt es auch oben die Druck auf der Oberseite des Flügels ($p_t$) und unten die Druck auf die Unterseite des Flügels ($p_b$). Auf diese Weise entsteht die Druckdifferenz auf einem Objekt ($\Delta p$)
das wiederum eine Auftriebskraft ($F_L$) erzeugt, um die durch die Körpermasse ($m$) mit die Gravitationsbeschleunigung ($g$) erzeugte Gravitationskraft auszugleichen.
Wenn ein Druckunterschied $\Delta p$ zwischen der Unter- und Oberseite eines Fl gels mit einer Fl che $S_w$ erzeugt wird, wird die resultierende Kraft als Auftriebskraft bezeichnet und wie folgt berechnet:
Diese Auftriebskraft entsteht als Folge des Druckunterschieds und ist verantwortlich f r den Flug eines Flugzeugs.
Mit dem bekannten Vektorfeld des Flusses um das Objekt entlang der gesamten Oberfl che ist es m glich, die Aerodynamische Zirkulation ($\Gamma$) durch Integration entlang eines geschlossenen Pfades zu berechnen, wie unten dargestellt:
Im Fall des Flusses, der ber das Objekt/den Fl gel str mt, ist es notwendig, den Startpunkt und den Endpunkt zu identifizieren, um die L nge des Weges die Obere Flügellänge ($l_t$) zu definieren:
Wenn wir annehmen, dass die Geschwindigkeit an der Oberseite ($v_t$) konstant ist, k nnen wir auf das Vorhandensein von ein Flügel-Höchstgeschwindigkeitsfaktor ($c_t$) schlie en, so dass zusammen mit die Geschwindigkeit in Bezug auf das Medium ($v$) gilt:
Im Fall des Flusses, der unter dem Objekt/Fl gel hindurchstr mt, ist es notwendig, den Startpunkt und den Endpunkt zu identifizieren, um die L nge des Weges die Länge des unteren Flügels ($l_b$) zu definieren:
Wenn wir annehmen, dass die Geschwindigkeit an der Unterseite ($v_b$) konstant ist, k nnen wir auf das Vorhandensein von ein Flügelbodengeschwindigkeitsfaktor ($c_b$) schlie en, so dass zusammen mit die Geschwindigkeit in Bezug auf das Medium ($v$) gilt:
Um eine vereinfachte Sch tzung der Zirkulation zu erhalten, k nnen wir annehmen, dass die Geschwindigkeit auf dem oberen Teil des Umfangs die Geschwindigkeit an der Oberseite ($v_t$) und auch auf dem unteren Teil die Geschwindigkeit an der Unterseite ($v_b$) konstant ist. Wenn diese Geschwindigkeiten proportional zu die Geschwindigkeit in Bezug auf das Medium ($v$) mit der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$) und der Flügelbodengeschwindigkeitsfaktor ($c_b$) sind und die L ngen die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) sind, wird die Aerodynamische Zirkulation ($\Gamma$) wie folgt berechnet:
Basierend auf den Arbeiten von Kutta [1] und Joukowski [2] wurde ein Theorem entwickelt, das die Verbindung zwischen die Aerodynamische Zirkulation ($\Gamma$) und die Auftriebskraft ($F_L$) durch die Spannweite der Flügel ($L$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wie folgt zeigt:
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben.", Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." , Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
Die Auftriebskraft ($F_L$) steht in Beziehung zu die Aerodynamische Zirkulation ($\Gamma$), die Spannweite der Flügel ($L$) zu die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wie folgt:
Daher erhalten wir mit der Sch tzung von die Aerodynamische Zirkulation ($\Gamma$) in Bezug auf der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) folgendes:
Die Oberfläche, die Auftrieb erzeugt ($S_w$) ist gleich die Spannweite der Flügel ($L$) geteilt durch der Flügelbreite ($w$), wobei letzteres als Durchschnitt von die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$) gesch tzt werden kann, was zu folgendem Ergebnis f hrt:
Der Koeffizient Fahrstuhl ($C_L$) kann basierend auf die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$) und der Flügelbodengeschwindigkeitsfaktor ($c_b$) wie folgt berechnet werden:
Die Aerodynamische Zirkulation ($\Gamma$) wird schlie lich in einer Berechnung zusammengefasst, die die Oberfläche, die Auftrieb erzeugt ($S_w$), die Spannweite der Flügel ($L$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) durch die Gleichung umfasst:
Um einen h heren Druck unterhalb als oberhalb des Fl gels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck ber dem Fl gel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel gesch tzt werden:
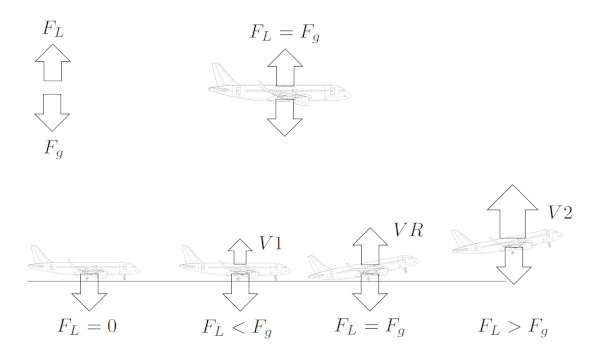
Damit ein Raumschiff oder ein Vogel in der Luft bleiben kann, muss die Erdanziehungskraft ($F_g$) die Schwerkraft ausgleichen, die durch die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) definiert ist. Mit anderen Worten, es muss sein:
Dies ist eine vereinfachte Situation, die nicht ber cksichtigt, dass der Widerstand auch eine Auftriebskraft erzeugen kann.
Aus Messungen geht hervor, dass der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist:
Nach einem bestimmten Winkel nimmt die Kurve ab und erreicht schlie lich den Wert Null. Dies liegt daran, dass ber diesem kritischen Winkel die Wirbel vollst ndig die obere Fl che des Fl gels bedecken und somit der Auftrieb verloren geht. Dieses Ph nomen wird als \"Str mungsabriss\" bezeichnet.
Die Bedingung f r das Erreichen des Fluges wird erf llt, wenn die Auftriebskraft ($F_L$) dem Gewicht des Flugzeugs oder Vogels entspricht, das aus die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) berechnet wird. Dies wird durch ausreichende Werte von ERROR:6110,0, die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$) erreicht, wobei letzterer Koeffizient der anpassbare Faktor ist. Im Fall von Flugzeugen k nnen Piloten den Wert von der Koeffizient Fahrstuhl ($C_L$) mithilfe von Klappen ndern, deren Wert folgende Bedingung erf llen muss:
Die Klappen werden durch ndern des Winkels eingestellt, den der Fl gel zur Flugrichtung bildet, bekannt als Anstellwinkel.
Da der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist, kann der erforderliche Winkel zur Erzeugung ausreichender Auftriebskraft bei einer gegebenen Geschwindigkeit $v$ berechnet werden:
wobei $m$ die Masse, $g$ die Erdbeschleunigung, $\rho$ die Dichte des Mediums, $S_w$ die Fl gelfl che und $c$ die Proportionalit tskonstante zwischen dem Auftriebskoeffizienten und dem Anstellwinkel sind.
ID:(463, 0)