User: 
Lift
Storyboard 
The flow around a wing leads to the formation of whirlpools that, depending on the shape and angle of the wing with respect to the flow, can cause whirlpools in a section of these. If volume elements around the wing are considered and it is assumed that energy conservation can be madly assumed, different speeds will have to lead to different pressures (Bernoulli) on the surface.
The sum of all pressures on the surface in the vertical direction, both on the wing (downward force) and under the wing (upward force) leads to a total force that we call lift. If this is positive we can overcome gravity and make the body (plane / bird) rise.
ID:(463, 0)
Mechanisms
Iframe
Mechanisms
ID:(15181, 0)
Wing generating lift
Description
Upon observing the average flow around a wing, one can notice that the lines above the wing are longer than those below it. In simplified terms, it is argued that due to this longer path, the speed at the top ($v_t$) is expected to be greater than the speed at the bottom ($v_b$), although both are higher than the speed with respect to the medium ($v$).
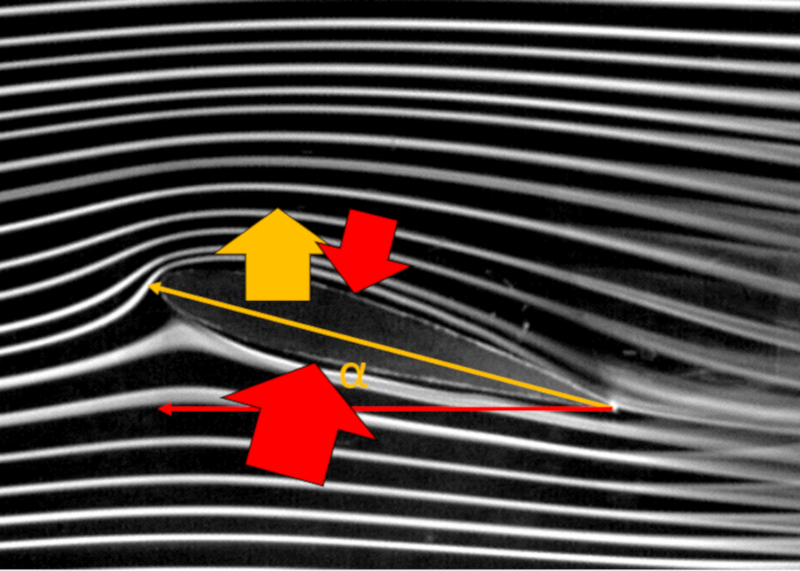
If Bernoulli's law is applicable, the difference in velocities would result in a difference in pressures acting on the wing. In particular, if the speed at the top ($v_t$) is greater, its corresponding the pressure on top of wing ($p_t$) would be lower than with the speed at the bottom ($v_b$) and its corresponding the pressure on the bottom of the wing ($p_b$). This would imply the existence of a the lift force ($F_L$) due to the effect of this pressure difference.
However, as seen towards the end of the wing profile (right side), turbulence forms, limiting the applicability of Bernoulli's principle. Specifically, it should be considered that in a certain portion of the wing's perimeter, it may not be applicable, and there will be no contribution to lift.
ID:(11075, 0)
Circulation around an object
Concept
To define circulation, we must first establish the path that will be followed around the object/wing in a counterclockwise direction, as indicated in the following image:
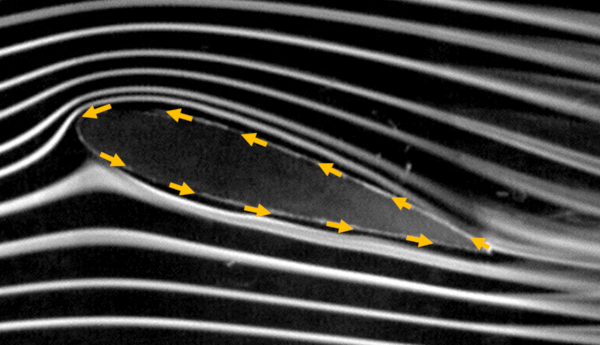
Circulation is defined as the product of the perimeter around the object and the projection of velocity onto the surface. Since this velocity projection can vary along the perimeter, we must sum it through infinitesimal elements of the perimeter, where the velocity projection is calculated using the dot product between it and the perimeter element. Graphically, this is represented as follows:
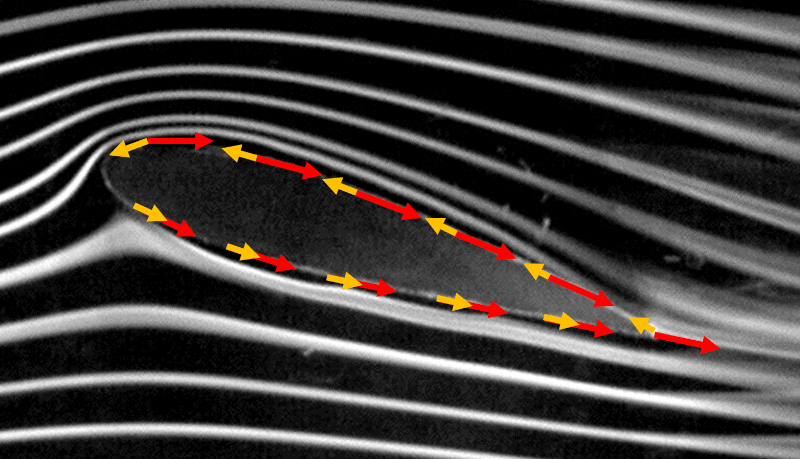
Mathematically, this is expressed through the closed line integral of the aforementioned dot product:
| $ \Gamma =\displaystyle\oint_C \vec{v} \cdot d\vec{l} $ |
Since the sum is performed counterclockwise, in the upper part, the direction in which the perimeter elements point is opposite to the direction of velocity. In the lower part, both point in the same direction, leading to the upper part partially canceling out the lower part.
ID:(1167, 0)
KuttaJoukowski theorem
Concept
The relationship between the aerodynamic circulation ($\Gamma$) and the flow around the object is established through the Kutta-Joukowski theorem, enabling the calculation of the lift force ($F_L$) using the wing span ($L$), the density ($\rho$), and the speed with respect to the medium ($v$) as follows:
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
By simplifying the modeling of the flow around the object, it becomes feasible to estimate circulation using the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$) with the equation:
| $ \Gamma = \displaystyle\frac{ S_w }{2 L } C_L v ^2$ |
Consequently, the lift force ($F_L$) can be approximated with the equation:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
Here, the coefficient of lift ($C_L$) encapsulates the aerodynamic effects of the object.
[1] "Über die Aufgabe der Flügeltheorie und ein neues Verfahren zur Herleitung derselben." (On the task of wing theory and a new method for its derivation.), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1902)
[2] "Über die Erhaltung des Luftkreises um ein Profil." (On the conservation of the air circle around a profile.), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1904)
ID:(1168, 0)
Lift coefficient
Description
The lift coefficient is a function of the angle of attack and typically follows the trend indicated in the following figure:
In the illustrated case, the slope is approximately 1.5 per 15 degrees, which corresponds to 0.1 1/degree or 5.73 1/radian.
ID:(7148, 0)
Lift force in the flow
Concept
The difference in pressure between the lower and upper surfaces of the wing generates the lift force, indicated by an arrow perpendicular to the wing's surface. This force opposes the gravitational force acting downward:
Birds or aircraft are able to fly when the lift force exceeds the gravitational force.
ID:(7036, 0)
The takeoff of a plane
Concept
The difference in pressure between the lower and upper surfaces of the wing generates the lift force, indicated by an arrow perpendicular to the wing's surface. This force opposes the gravitational force acting downward:
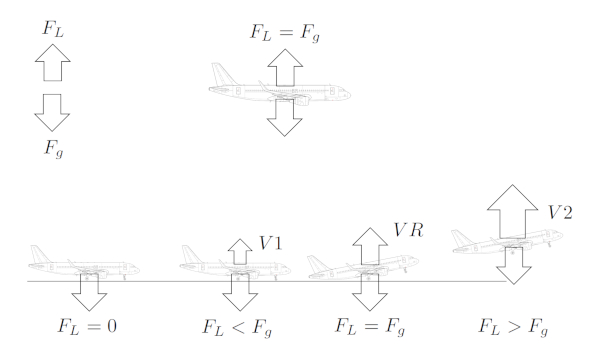
Birds or aircraft are able to fly when the lift force exceeds the gravitational force.
ID:(15157, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$
alpha =2* m * g /( c * rho * S_w * v ^2)
$ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$
C_L = 4*( c_t * l_t - c_b * l_b )/( l_t + l_b )
$ C_L = c \alpha $
C_L = c * alpha
$ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$
C_L =2* m * g /( rho * S_w * v ^2)
$ \Delta p = p_b - p_t $
Dp = p_b - p_t
$ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$
F_ L / L = - rho * v * Gamma
$ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$
F_ L = rho * L *( c_b * l_b - c_t l_t )* v ^2
$ F_g = m g $
F_g = m * g
$ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ F_L = S_w \Delta p $
F_L = S_w * Dp
$ \Gamma = ( c_b l_b - c_t l_t ) v $
Gamma = ( c_b * l_b - c_t * l_t )* v
$ \Gamma =\displaystyle\oint_C \vec{v} \cdot d\vec{l} $
Gamma = @CINT( &v , l )
$ \Gamma = \displaystyle\frac{ S_w }{2 L } C_L v ^2$
Gamma = S_w * C_L * v ^2/(2 * L )
$ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$
S_w = L *( l_t + l_b )/2
$ v_b = c_b v $
v_b = c_b * v
$ v_t = c_t v $
v_t = c_t * v
ID:(15184, 0)
Lift
Equation
When an object is immersed in a flow with a constant energy density, it divides the flow into an upper one with the speed at the top ($v_t$) and a lower one with the speed at the bottom ($v_b$). Velocity is related to the pressure generated, so there is also the pressure on top of wing ($p_t$) at the upper part and the pressure on the bottom of the wing ($p_b$) at the lower part. In this way, the pressure difference on an object ($\Delta p$)
| $ \Delta p = p_b - p_t $ |
is generated, which in turn produces ($$) to counteract the gravitational force generated by the body mass ($m$) with the gravitational Acceleration ($g$).
ID:(1173, 0)
Lift force due to pressure difference
Equation
If a pressure difference $\Delta p$ is achieved between the lower and upper surfaces of a wing with an area $S_w$, the resulting force is called the lift force and is calculated as follows:
| $ F_L = S_w \Delta p $ |
This lift force is generated as a result of the pressure difference and is responsible for supporting the flight of an aircraft.
ID:(4416, 0)
Circulation around an object
Equation
With the flow around the object known in its vectorial form along the entire surface, it is possible to calculate the aerodynamic circulation ($\Gamma$) through integration along a closed path, as shown below:
| $ \Gamma =\displaystyle\oint_C \vec{v} \cdot d\vec{l} $ |
This formulation assumes an infinitely extended body in the direction perpendicular to the flow field.
ID:(15194, 0)
Top wing speed
Equation
In the case of the flow passing over the object/wing, it is necessary to identify the starting point and the endpoint to define the length of the path the upper wing length ($l_t$):
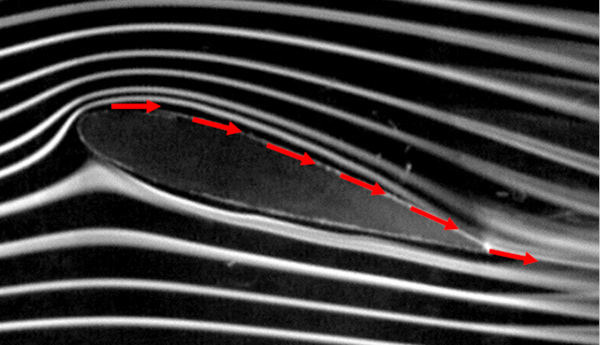
If we assume that the speed at the top ($v_t$) is constant, we can infer the existence of a wing top speed factor ($c_t$) such that, along with the speed with respect to the medium ($v$), we have:
| $ v_t = c_t v $ |
ID:(15152, 0)
Lower wing speed
Equation
In the case of the flow passing beneath the object/wing, it is necessary to identify the starting point and the endpoint to define the length of the path the bottom wing length ($l_b$):
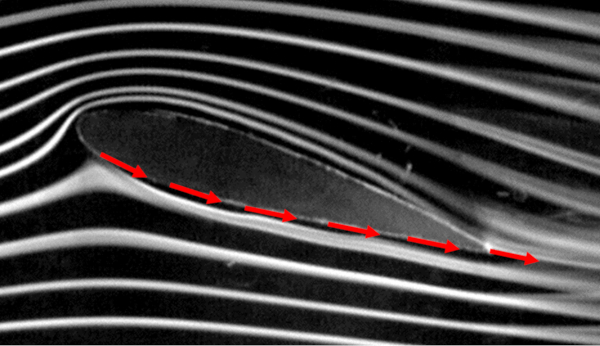
If we assume that the speed at the bottom ($v_b$) is constant, we can infer the existence of a wing bottom speed factor ($c_b$) such that, along with the speed with respect to the medium ($v$), we have:
| $ v_b = c_b v $ |
ID:(15153, 0)
Estimation of circulation around an object
Equation
To obtain a simplified estimation of circulation, we can assume that velocity is constant on the upper part of the perimeter the speed at the top ($v_t$) and also on the lower part the speed at the bottom ($v_b$). If these velocities are proportional to the speed with respect to the medium ($v$) with the wing top speed factor ($c_t$) and the wing bottom speed factor ($c_b$), and the lengths are the upper wing length ($l_t$) and the bottom wing length ($l_b$), then the aerodynamic circulation ($\Gamma$) is calculated as follows:
| $ \Gamma = ( c_b l_b - c_t l_t ) v $ |
The aerodynamic circulation ($\Gamma$) is defined in terms of the lengths the upper wing length ($l_t$) and the bottom wing length ($l_b$) along with the velocities the speed at the top ($v_t$) and the speed at the bottom ($v_b$), as follows:
$\Gamma = -l_t v_t + l_b v_b$
If the speed at the top ($v_t$) is proportional to the wing top speed factor ($c_t$) with respect to the speed with respect to the medium ($v$):
| $ v_t = c_t v $ |
and the speed at the bottom ($v_b$) is proportional to the wing bottom speed factor ($c_b$) with respect to the speed with respect to the medium ($v$):
| $ v_b = c_b v $ |
we can express it as:
$\Gamma = -l_t c_t v + l_b c_b v$
This leads us to the following equation:
| $ \Gamma = ( c_b l_b - c_t l_t ) v $ |
ID:(15193, 0)
KuttaJoukowski theorem
Equation
From the works of Kutta [1] and Joukowski [2], a theorem was developed that shows the association between the aerodynamic circulation ($\Gamma$) and the lift force ($F_L$) through the wing span ($L$), the density ($\rho$), and the speed with respect to the medium ($v$) as follows:
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
[1] "Über die Aufgabe der Flügeltheorie und ein neues Verfahren zur Herleitung derselben." (On the task of wing theory and a new method for its derivation.), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1902)
[2] "Über die Erhaltung des Luftkreises um ein Profil." (On the conservation of the air circle around a profile.), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (1904)
ID:(1166, 0)
Lift force with circulation
Equation
The lift force ($F_L$) is related to the aerodynamic circulation ($\Gamma$), the wing span ($L$) to the density ($\rho$), and the speed with respect to the medium ($v$) as follows:
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
Therefore, with the estimation of the aerodynamic circulation ($\Gamma$) in terms of the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), and the bottom wing length ($l_b$), we have:
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
The lift force ($F_L$) is related to the aerodynamic circulation ($\Gamma$), the wing span ($L$), the density ($\rho$), and the speed with respect to the medium ($v$) as follows:
| $ \displaystyle\frac{ F_L }{ L } = - \rho v \Gamma$ |
Since the aerodynamic circulation ($\Gamma$) is related to the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), and the bottom wing length ($l_b$) as follows:
| $$ |
We can conclude that:
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
ID:(15156, 0)
Wing surface
Equation
The surface that generates lift ($S_w$) is equal to the wing span ($L$) divided by the wing width ($w$), and the latter can be estimated as the average of the upper wing length ($l_t$) and the bottom wing length ($l_b$), resulting in:
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
The lift force ($F_L$) depends on the surface that generates lift ($S_w$) and the pressure difference on an object ($\Delta p$) as per
| $ F_L = S_w \Delta p $ |
in the expression for the lift force ($F_L$) with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$)
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
contains the factor the wing span ($L$) that is associated with the surface that generates lift ($S_w$). However, both can be associated if we consider the wing's width as the average of the upper wing length ($l_t$) and the bottom wing length ($l_b$). This leads us to obtain
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
ID:(15154, 0)
Lift coefficient model
Equation
The coefficient of lift ($C_L$) can be calculated based on the upper wing length ($l_t$), the bottom wing length ($l_b$), the wing top speed factor ($c_t$), and the wing bottom speed factor ($c_b$) as follows:
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
The lift force ($F_L$) along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$) is found in
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
If we consider the surface that generates lift ($S_w$) given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$)
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
we can rewrite the equation for the lift force ($F_L$) as
$F_L =\displaystyle\frac{1}{2} \rho S_w \displaystyle\frac{4(c_bl_b-c_tl_t)}{l_b+l_t} v^2$
which allows us to introduce the lift coefficient:
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
ID:(15155, 0)
Calculation of circulation around an object
Equation
The aerodynamic circulation ($\Gamma$) is ultimately summarized in a calculation involving the surface that generates lift ($S_w$), the wing span ($L$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) through the equation:
| $ \Gamma = \displaystyle\frac{ S_w }{2 L } C_L v ^2$ |
When relating the aerodynamic circulation ($\Gamma$) to the wing bottom speed factor ($c_b$), the wing top speed factor ($c_t$), the bottom wing length ($l_b$), and the upper wing length ($l_t$), we have:
| $ \Gamma = ( c_b l_b - c_t l_t ) v $ |
By estimating the surface that generates lift ($S_w$) with the wing span ($L$) using:
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
and calculating the coefficient of lift ($C_L$) with:
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
The result is:
| $ \Gamma = \displaystyle\frac{ S_w }{2 L } C_L v ^2$ |
ID:(15195, 0)
Lift force
Equation
To generate higher pressure below than above the wing and generate lift, Bernoulli's principle is employed, correcting for the lack of energy density conservation using ($$). The pressure over the wing, the lift force ($F_L$), can be estimated using the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) through the following formula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
The lift force ($F_L$), along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$), is found in
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
If we consider the surface that generates lift ($S_w$), given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
and for the coefficient of lift ($C_L$), defined as
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
we obtain
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Flight condition
Equation
In order for a spacecraft or a bird to remain in flight, the gravitational force ($F_g$) must counteract the force of gravity, which is defined by the body mass ($m$) and the gravitational Acceleration ($g$). In other words, it must be:
| $ F_g = m g $ |
This is a simplified situation that does not take into account that the force of resistance can also generate a lift force.
ID:(14515, 0)
Lift constant
Equation
From measurements, it is concluded that the lift coefficient $C_L$ is proportional to the angle of attack $\alpha$:
| $ C_L = c \alpha $ |
After a certain angle, the curve decreases until it reaches zero. This is because beyond that critical angle, the vortices fully cover the upper surface of the wing, leading to a loss of lift. This phenomenon is known as \"stall\".
ID:(4441, 0)
Equilibrium lifting coefficient
Equation
The condition for achieving flight is met when the lift force ($F_L$) equals the weight of the aircraft or bird, which is calculated from the body mass ($m$) and the gravitational Acceleration ($g$). This is achieved with sufficient values of speed with respect to the medium ($v$), the surface that generates lift ($S_w$), and the coefficient of lift ($C_L$), where the latter coefficient is the adjustable factor. In the case of aircraft, pilots can modify the value of the coefficient of lift ($C_L$) using flaps, whose value must satisfy:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
The lift force ($F_L$) along with the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) is represented as
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
which, along with the body mass ($m$) and the gravitational Acceleration ($g$), must be equal to:
| $ F_g = m g $ |
that is:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
resulting in:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Flaps are adjusted by changing the angle that the wing makes with the direction of flight, known as the angle of attack.
ID:(4442, 0)
Attack angle
Equation
Since the lift coefficient $C_L$ is proportional to the angle of attack $\alpha$, we can calculate the necessary angle to achieve sufficient lift for a given velocity $v$:
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
The coefficient of lift ($C_L$) is calculated with the body mass ($m$), the gravitational Acceleration ($g$), the surface that generates lift ($S_w$), the density ($\rho$), and the speed with respect to the medium ($v$) as follows:
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Therefore, with the proportionality constant coefficient sustainability ($c$) and the angle of attack of a wing ($\alpha$),
| $ C_L = c \alpha $ |
we have
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
where $m$ is the mass, $g$ is the gravitational acceleration, $\rho$ is the density of the medium, $S_w$ is the wing area, and $c$ is the proportionality constant between the lift coefficient and the angle of attack.
ID:(4443, 0)