Resistência
Storyboard 
O fluxo em torno de uma asa leva à formação de vórtices que, dependendo da forma e do ângulo da asa em relação ao fluxo, pode originar vórtices em uma seção dela. Se considerarmos elementos de volume em torno da asa e assumirmos que a conservação de energia pode ser localmente aplicada, diferentes velocidades resultarão em diferentes pressões (Bernoulli) na superfície.
A soma de todas as pressões na superfície na direção do voo, tanto à frente da asa (força para trás) quanto atrás da asa (força para frente), resulta em uma força total que chamamos de resistência. Para impulsionar um corpo (avião/ave), é necessário que a propulsão supere essa força de resistência.
ID:(464, 0)
Resistência
Storyboard 
O fluxo em torno de uma asa leva à formação de vórtices que, dependendo da forma e do ângulo da asa em relação ao fluxo, pode originar vórtices em uma seção dela. Se considerarmos elementos de volume em torno da asa e assumirmos que a conservação de energia pode ser localmente aplicada, diferentes velocidades resultarão em diferentes pressões (Bernoulli) na superfície. A soma de todas as pressões na superfície na direção do voo, tanto à frente da asa (força para trás) quanto atrás da asa (força para frente), resulta em uma força total que chamamos de resistência. Para impulsionar um corpo (avião/ave), é necessário que a propulsão supere essa força de resistência.
Variáveis
Cálculos
Cálculos
Equações
La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em
Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),
e para o coeficiente de elevação ($C_L$), definido como
obtemos
De maneira semelhante forma como a equa o para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)
nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) ser equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no c lculo de la força de resistência ($F_W$):
O coeficiente de arrasto medido e, em fluxos turbulentos sobre corpos aerodin micos, geralmente se obt m valores em torno de 0.4.
Utilizando as rela es de la força de resistência total ($F_R$) com la força de elevação ($F_L$), la força de resistência ($F_W$) e o aceleração máxima ($\alpha$):
podemos calcular a for a de resist ncia utilizando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$):
e a for a de sustenta o com la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$):
utilizando a rela o para o coeficiente de elevação ($C_L$) com la constante de proporcionalidade do coeficiente de sustentação ($c$):
usando a rela o para o seno do pequeno ngulo de ataque $\alpha$:
e o cosseno:
com a condi o de equilibrar o peso do p ssaro ou aeronave para la massa corporal ($m$) e la aceleração gravitacional ($g$):
obtemos:
A componente horizontal da sustenta o corresponde for a $F_L$ multiplicada pelo seno do ngulo de ataque $\alpha$:
$F_L \sin\alpha $
e a componente horizontal da resist ncia corresponde for a $F_W$ multiplicada pelo cosseno do ngulo de ataque $\alpha$:
$F_W \cos\alpha $
Portanto, a for a total de resist ncia calculada da seguinte forma:
O seno pode ser calculado usando um polin mio da forma:
$\sin \alpha = \alpha - \displaystyle\frac{1}{3!}\alpha^3 + \displaystyle\frac{1}{5!}\alpha^5 \ldos$
Para valores pequenos de o aceleração máxima ($\alpha$) ($\alpha \ll 1$), os termos com pot ncias superiores s o negligenci veis, e obtemos:
O cosseno pode ser calculado usando um polin mio da forma:
$\cos \alpha = 1 - \displaystyle\frac{1}{2!}\alpha^2 + \displaystyle\frac{1}{4!}\alpha^4 \ldots$
Para valores pequenos de o aceleração máxima ($\alpha$) ($\alpha \ll 1$), os termos com pot ncias mais altas s o negligenci veis, e obtemos:
Exemplos
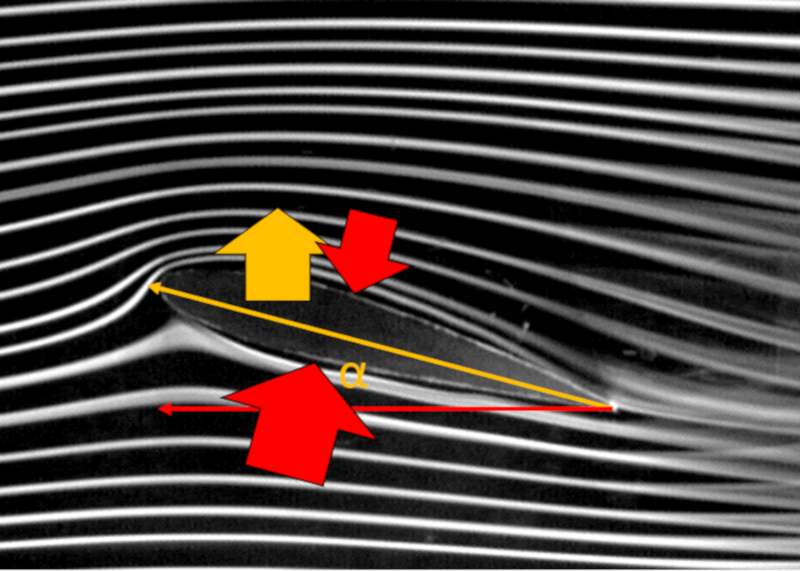
Ao observar o fluxo m dio ao redor de uma asa, pode-se notar que as linhas acima da asa s o mais longas do que as abaixo dela. Em termos simplificados, argumenta-se que devido a esse caminho mais longo, espera-se que la velocidade no topo ($v_t$) seja maior do que la velocidade na parte inferior ($v_b$), embora ambos sejam superiores a la velocidade em relação ao meio ($v$).
Se a lei de Bernoulli for aplic vel, a diferen a de velocidades resultaria em uma diferen a de press es atuando na asa. Em particular, se la velocidade no topo ($v_t$) for maior, seu correspondente la pressão no topo da asa ($p_t$) seria menor do que com la velocidade na parte inferior ($v_b$) e seu correspondente la pressão na parte inferior da asa ($p_b$). Isso implicaria na exist ncia de um la força de elevação ($F_L$) devido ao efeito dessa diferen a de press o.
No entanto, como observado em dire o ao final do perfil da asa (lado direito), a turbul ncia se forma, limitando a aplicabilidade do princ pio de Bernoulli. Especificamente, deve-se considerar que em uma certa parte do per metro da asa, a aplicabilidade pode ser limitada, e n o haver contribui o para a sustenta o.
O objeto n o apenas gera sustenta o, mas tamb m cria resist ncia ao fluxo de ar ao seu redor. Embora a aplica o direta do princ pio de Bernoulli possa n o ser vi vel, ainda podemos compreender o tipo de efeito a esperar, mesmo que seja necess rio model -lo de maneira diferente. Nesse contexto, na ponta da asa, a velocidade zero, resultando em press o m xima. Da mesma forma, na extremidade traseira do objeto, a velocidade m xima, resultando em press o m nima. Isso gera uma press o que se op e ao movimento do objeto para a frente, correspondendo resist ncia.
No entanto, importante observar que esse argumento apenas parcialmente correto. Em particular, a turbul ncia gerada na extremidade traseira da asa, o que complica o argumento de alta velocidade e desafia a aplica o do princ pio de Bernoulli.
Seguindo a abordagem de modelagem usada para o levantamento, podemos assumir que o teorema de Kutta-Joukowski, no qual la força de elevação ($F_L$) com la densidade ($\rho$), la velocidade em relação ao meio ($v$) e la circulação aerodinâmica ($\Gamma$), o seguinte:
Podemos assumir que ele vetorial, o que significa que possui uma componente vertical que explica o levantamento e uma componente horizontal que modela a resist ncia.
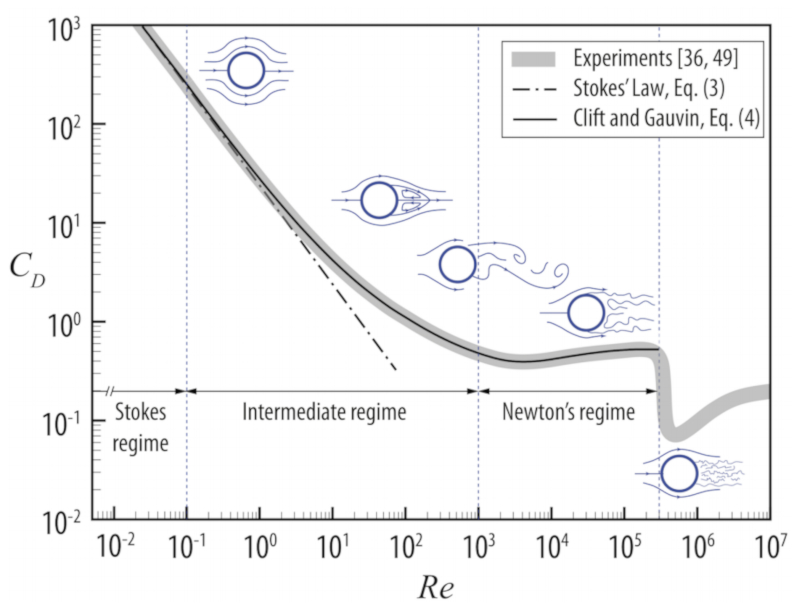
O coeficiente de resist ncia $C_d$ frequentemente uma fun o do n mero de Reynolds $Re$. No caso de uma esfera, o coeficiente de resist ncia assume a forma:
Na faixa de baixos n meros de Reynolds, o coeficiente de resist ncia inversamente proporcional velocidade $1/v$, o que significa que nessa faixa a for a de arrasto proporcional velocidade (Lei de Stokes).
Na faixa de altos n meros de Reynolds, o coeficiente de resist ncia se torna constante, resultando em uma for a de arrasto proporcional ao quadrado da velocidade. No entanto, importante destacar que h uma queda brusca no coeficiente, indicando uma situa o em que a zona turbulenta diminui.
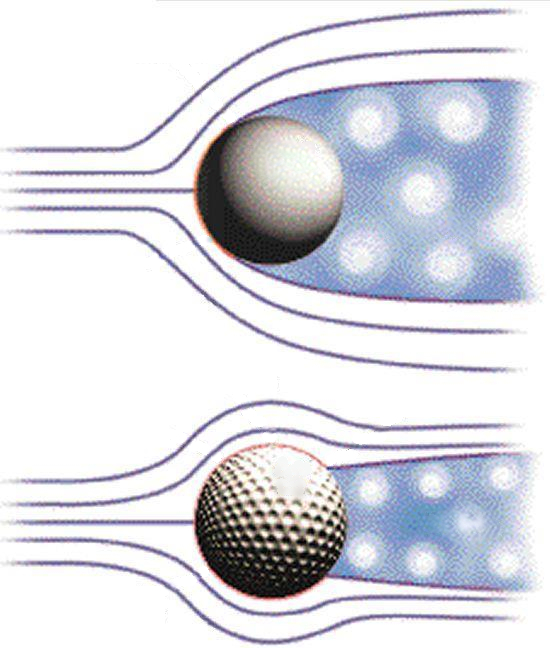
Para reduzir a resist ncia de uma bola, necess rio aumentar o n mero de Reynolds para aproveitar a diminui o do coeficiente de resist ncia. Isso pode ser alcan ado introduzindo ranhuras, como as encontradas em uma bola de golfe. Essas ranhuras atuam como pequenos separadores, mantendo a camada de ar aderida bola e prolongando o tempo em que o fluxo permanece linear, reduzindo assim a rea que gera a resist ncia.
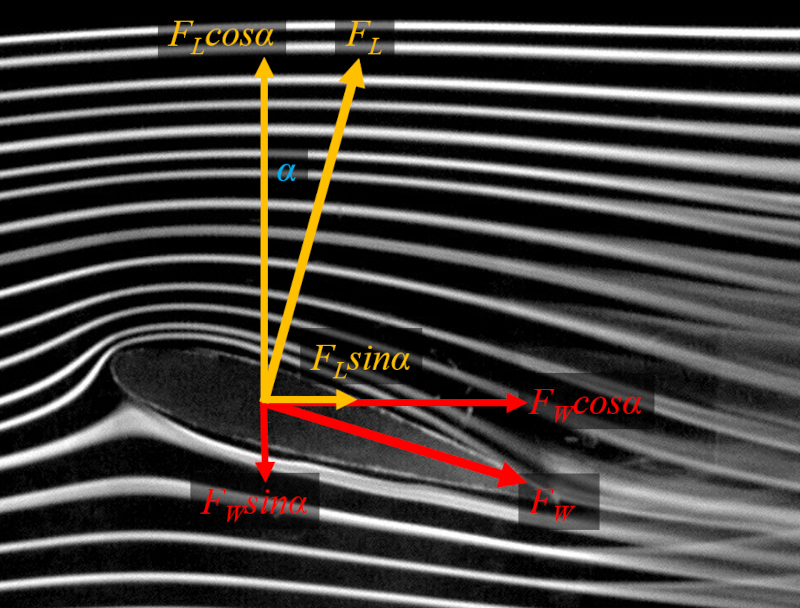
Ao inclinar a asa, n o apenas gera sustenta o, mas tamb m produz uma componente de resist ncia, j que a dire o da sustenta o ortogonal superf cie da asa. Se representarmos graficamente la força de elevação ($F_L$), la força de resistência ($F_W$) e o aceleração máxima ($\alpha$), obtemos:
A partir dos trabalhos de Kutta [1] e Joukowski [2], foi desenvolvido um teorema que mostra a associa o entre la circulação aerodinâmica ($\Gamma$) e la força de elevação ($F_L$) atrav s de la envergadura das asas ($L$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$) da seguinte forma:
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sobre a tarefa da teoria de asas e um novo m todo para sua deriva o), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sobre a conserva o do c rculo de ar ao redor de um perfil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
Para gerar uma press o maior abaixo do que acima da asa e gerar sustenta o, utiliza-se o princ pio de Bernoulli, corrigindo a falta de conserva o da densidade de energia com um coeficiente de elevação ($C_L$). A press o sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) atrav s da seguinte f rmula:
La força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) de acordo com o seguinte f rmula:
A for a total de resist ncia composta pelas componentes horizontais da for a de resist ncia do perfil da asa $F_W$ e da for a de sustenta o $F_L$, que podem ser calculadas a partir do ngulo de ataque $\alpha$:
A partir de medi es, conclui-se que o coeficiente de sustenta o $C_L$ proporcional ao ngulo de ataque $\alpha$:
Ap s um certo ngulo, a curva diminui at chegar a zero. Isso ocorre porque acima desse ngulo cr tico, os redemoinhos cobrem completamente a superf cie superior da asa, levando perda de sustenta o. Esse fen meno conhecido como \"stall\" (estol em portugu s).
Para ngulos pequenos, a fun o seno pode ser aproximada por uma reta que passa pela origem. Se o aceleração máxima ($\alpha$) for expresso em radianos, a inclina o desta reta igual a um, e obtemos:
Para valores pequenos de o aceleração máxima ($\alpha$), a fun o cosseno pode ser aproximada por uma par bola invertida que passa pela origem. Se o ngulo for expresso em radianos e for aproximadamente zero, obtemos:
Para calcular la força de resistência total ($F_R$), assumimos ngulos pequenos e consideramos uma situa o na qual o ngulo tal que mant m la massa corporal ($m$). Usando esta aproxima o e as vari veis o coeficiente de elevação ($C_L$), o coeficiente de resistência ($C_W$), la superfície que gera sustentação ($S_w$), o perfil total do objeto ($S_p$), la aceleração gravitacional ($g$), la constante de proporcionalidade do coeficiente de sustentação ($c$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$), obtemos a seguinte express o:
ID:(464, 0)