Widerstand
Storyboard 
Die Umströmung eines Flügels führt zur Bildung von Strudeln, die je nach Form und Winkel des Flügels in Bezug auf die Strömung in einem Abschnitt davon Strudel verursachen können. Wenn Volumenelemente um den Flügel herum betrachtet werden und angenommen wird, dass Energieeinsparung toll angenommen werden kann, haben die unterschiedlichen Geschwindigkeiten unterschiedliche Drücke (Bernoulli) auf der Oberfläche.
Die Summe aller Drücke auf der Oberfläche in Flugrichtung, sowohl vor dem Flügel (Rückwärtskraft) als auch hinter dem Flügel (Vorwärtskraft), führt zu einer Gesamtkraft, die wir Widerstand nennen. Um einen Körper (Flugzeug / Vogel) antreiben zu können, muss der Vortrieb diese Widerstandskraft übertreffen.
ID:(464, 0)
Widerstand
Storyboard 
Die Umströmung eines Flügels führt zur Bildung von Strudeln, die je nach Form und Winkel des Flügels in Bezug auf die Strömung in einem Abschnitt davon Strudel verursachen können. Wenn Volumenelemente um den Flügel herum betrachtet werden und angenommen wird, dass Energieeinsparung toll angenommen werden kann, haben die unterschiedlichen Geschwindigkeiten unterschiedliche Drücke (Bernoulli) auf der Oberfläche. Die Summe aller Drücke auf der Oberfläche in Flugrichtung, sowohl vor dem Flügel (Rückwärtskraft) als auch hinter dem Flügel (Vorwärtskraft), führt zu einer Gesamtkraft, die wir Widerstand nennen. Um einen Körper (Flugzeug / Vogel) antreiben zu können, muss der Vortrieb diese Widerstandskraft übertreffen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
und f r der Koeffizient Fahrstuhl ($C_L$), definiert als
erhalten wir
hnlich wie die Gleichung f r die Auftriebskraft ($F_L$) unter Verwendung von die Dichte ($\rho$), der Koeffizient Fahrstuhl ($C_L$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Geschwindigkeit in Bezug auf das Medium ($v$) abgeleitet wurde
entspricht in dieser Analogie das, was die Oberfläche, die Auftrieb erzeugt ($S_w$) entspricht, der Gesamtobjektprofil ($S_p$) und der Koeffizient Fahrstuhl ($C_L$) entspricht der Widerstandskoeffizient ($C_W$), woraus die Widerstandskraft ($F_W$) berechnet wird:
Der Widerstandsbeiwert wird gemessen und bei turbulenten Str mungen ber aerodynamischen K rpern werden blicherweise Werte um 0,4 ermittelt.
Unter Verwendung der Beziehungen von die Gesamtwiderstandskraft ($F_R$) mit die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$) und der Anstellwinkel eines Flügels ($\alpha$) k nnen wir unter Verwendung der Widerstandskraft mit die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) und die Geschwindigkeit in Bezug auf das Medium ($v$):
und der Auftriebskraft mit die Oberfläche, die Auftrieb erzeugt ($S_w$) und der Koeffizient Fahrstuhl ($C_L$):
unter Verwendung der Beziehung f r der Koeffizient Fahrstuhl ($C_L$) mit die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$):
unter Verwendung der Beziehung f r den Sinus des kleinen Anstellwinkels $\alpha$:
und des Kosinus:
bei der Bedingung, das Gewicht des Vogels oder Flugzeugs f r die Körpermasse ($m$) und die Gravitationsbeschleunigung ($g$) auszubalancieren:
erhalten wir:
Die horizontale Komponente des Auftriebs entspricht der Kraft $F_L$ multipliziert mit dem Sinus des Anstellwinkels $\alpha$:
$F_L \sin\alpha $
und die horizontale Komponente des Widerstands entspricht der Kraft $F_W$ multipliziert mit dem Kosinus des Anstellwinkels $\alpha$:
$F_W \cos\alpha $
Daher wird die Gesamtwiderstandskraft wie folgt berechnet:
Das Sinus kann mithilfe eines Polynoms der Form berechnet werden:
$\sin \alpha = \alpha - \displaystyle\frac{1}{3!}\alpha^3 + \displaystyle\frac{1}{5!}\alpha^5 \ldots$
F r kleine Werte von der Anstellwinkel eines Flügels ($\alpha$) ($\alpha \ll 1$) sind die Terme mit h heren Potenzen vernachl ssigbar, und wir erhalten:
Der Kosinus kann mithilfe eines Polynoms der Form berechnet werden:
$\cos \alpha = 1 - \displaystyle\frac{1}{2!}\alpha^2 + \displaystyle\frac{1}{4!}\alpha^4 \ldots$
F r kleine Werte von der Anstellwinkel eines Flügels ($\alpha$) ($\alpha \ll 1$) sind die Terme mit h heren Potenzen vernachl ssigbar, und wir erhalten:
Beispiele
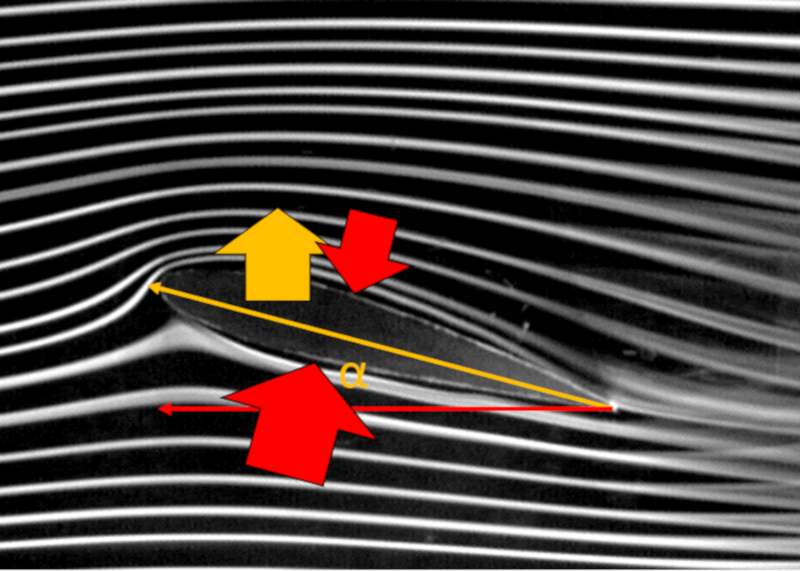
Beim Betrachten des durchschnittlichen Str mungsverhaltens um einen Fl gel f llt auf, dass die Linien ber dem Fl gel l nger sind als die unterhalb. In vereinfachten Begriffen wird argumentiert, dass aufgrund dieses l ngeren Wegs erwartet wird, dass die Geschwindigkeit an der Oberseite ($v_t$) gr er ist als die Geschwindigkeit an der Unterseite ($v_b$), obwohl beide h her sind als die Geschwindigkeit in Bezug auf das Medium ($v$).
Wenn das Bernoulli-Gesetz anwendbar ist, w rde die Geschwindigkeitsdifferenz zu einem Druckunterschied f hren, der auf den Fl gel wirkt. Insbesondere, wenn die Geschwindigkeit an der Oberseite ($v_t$) gr er ist, w re das zugeh rige die Druck auf der Oberseite des Flügels ($p_t$) niedriger als bei die Geschwindigkeit an der Unterseite ($v_b$) und das zugeh rige die Druck auf die Unterseite des Flügels ($p_b$). Dies w rde auf das Vorhandensein eines die Auftriebskraft ($F_L$) aufgrund dieses Druckunterschieds hinweisen.
Jedoch bildet sich gegen Ende des Profils des Fl gels (rechte Seite) Turbulenz, was die Anwendbarkeit des Bernoulli-Prinzips einschr nkt. Es sollte insbesondere ber cksichtigt werden, dass in einem bestimmten Teil des Umfangs des Fl gels die Anwendbarkeit nicht gegeben sein kann und somit keine Beitrag zur Auftrieb leistet.
Der Gegenstand erzeugt nicht nur Auftrieb, sondern erzeugt auch Widerstand gegen den Luftstrom in seiner Umgebung. Obwohl das direkte Anwenden des Bernoulli-Prinzips m glicherweise nicht m glich ist, k nnen wir dennoch verstehen, welche Art von Effekt zu erwarten ist, selbst wenn er auf andere Weise modelliert werden muss. In diesem Zusammenhang ist die Geschwindigkeit am Fl gelende null, was zu maximalem Druck f hrt. Ebenso ist am hinteren Ende des Objekts die Geschwindigkeit maximal und f hrt zu minimalem Druck. Dies erzeugt einen Druck, der der Vorw rtsbewegung des Objekts entgegenwirkt und somit dem Widerstand entspricht.
Es ist jedoch wichtig zu beachten, dass dieses Argument nur teilweise korrekt ist. Insbesondere wird am hinteren Ende des Fl gels Turbulenz erzeugt, was das Argument der hohen Geschwindigkeit kompliziert und die Anwendung des Bernoulli-Prinzips in Frage stellt.
Unter Ber cksichtigung des Modellierungsansatzes f r den Auftrieb k nnen wir annehmen, dass das Kutta-Joukowski-Theorem, in dem die Auftriebskraft ($F_L$) mit die Dichte ($\rho$), die Geschwindigkeit in Bezug auf das Medium ($v$) und die Aerodynamische Zirkulation ($\Gamma$) wie folgt ist:
Wir k nnen annehmen, dass es vektoriell ist, was bedeutet, dass es eine vertikale Komponente f r den Auftrieb und eine horizontale Komponente f r den Widerstand hat.
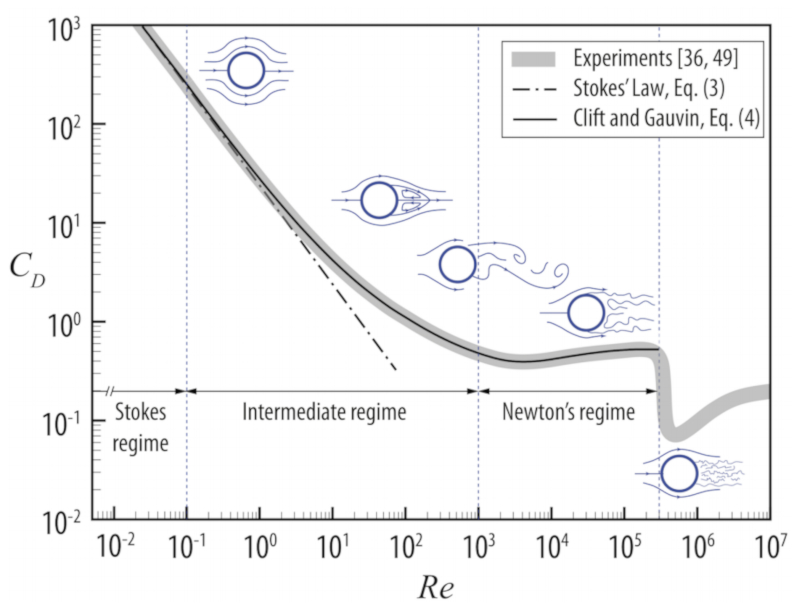
Der Widerstandsbeiwert $C_w$ ist oft eine Funktion der Reynoldszahl $Re$. Im Fall einer Kugel hat der Widerstandsbeiwert die Form:
Im Bereich niedriger Reynoldszahlen ist der Widerstandsbeiwert proportional zum Kehrwert der Geschwindigkeit $1/v$, sodass in diesem Bereich die Widerstandskraft proportional zur Geschwindigkeit ist (Stokessches Gesetz).
Im Bereich hoher Reynoldszahlen wird der Widerstandsbeiwert konstant, was bedeutet, dass die Widerstandskraft proportional zum Quadrat der Geschwindigkeit ist. Es ist jedoch wichtig zu beachten, dass es einen pl tzlichen Abfall des Koeffizienten gibt, der auf eine Situation hinweist, in der die turbulente Zone abnimmt.
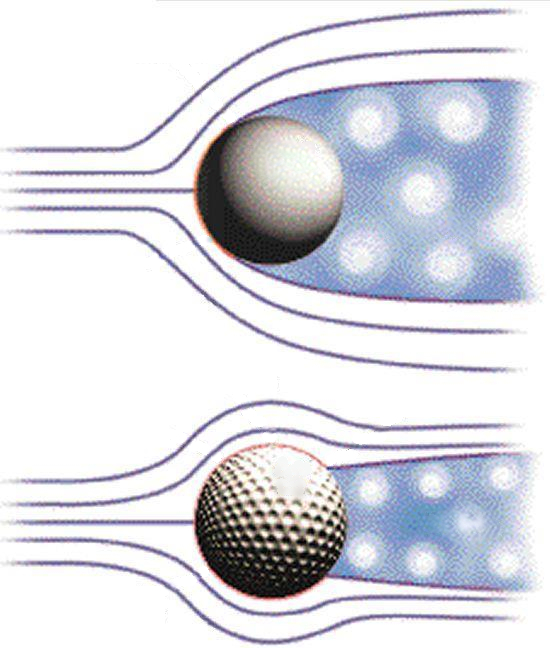
Wenn das Ziel darin besteht, den Widerstand eines Balls zu verringern, ist es notwendig, die Reynolds-Zahl zu erh hen, um von der Verringerung des Widerstandsbeiwerts zu profitieren. Dies kann durch Einf hrung von Rillen, wie sie bei einem Golfball vorhanden sind, erreicht werden. Diese Rillen wirken wie kleine Trennelemente, die die Luftschicht am Ball halten und den Fluss l nger linear halten, wodurch der Bereich, der den Widerstand erzeugt, verringert wird.
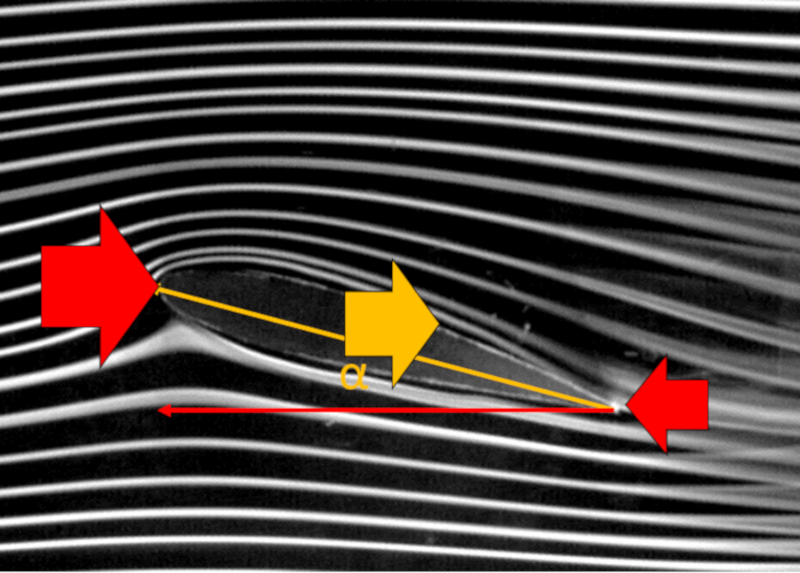
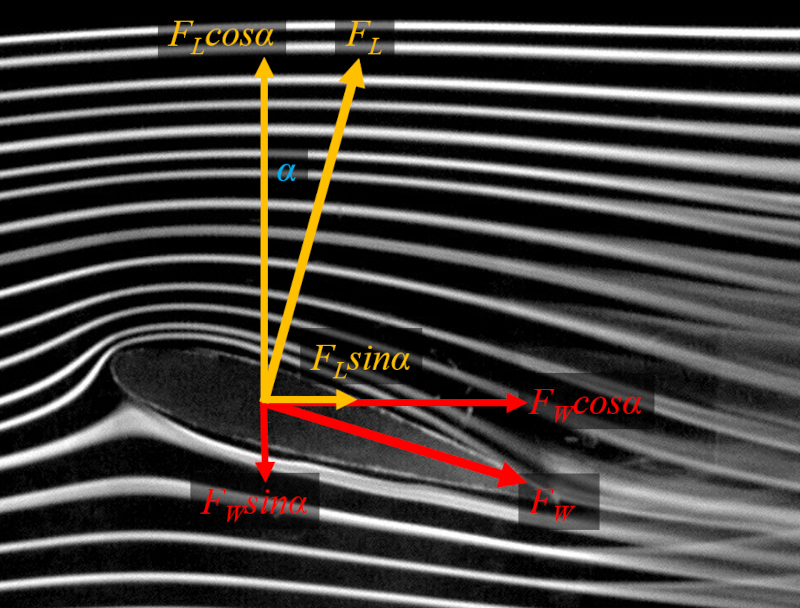
Wenn der Fl gel geneigt wird, erzeugt er nicht nur Auftrieb, sondern auch einen Teil des Widerstands, da die Richtung des Auftriebs orthogonal zur Fl gelfl che verl uft. Wenn wir die Auftriebskraft ($F_L$), die Widerstandskraft ($F_W$) und der Anstellwinkel eines Flügels ($\alpha$) grafisch darstellen, erhalten wir:
Basierend auf den Arbeiten von Kutta [1] und Joukowski [2] wurde ein Theorem entwickelt, das die Verbindung zwischen die Aerodynamische Zirkulation ($\Gamma$) und die Auftriebskraft ($F_L$) durch die Spannweite der Flügel ($L$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) wie folgt zeigt:
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben.", Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." , Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
Um einen h heren Druck unterhalb als oberhalb des Fl gels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck ber dem Fl gel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel gesch tzt werden:
Die Widerstandskraft ($F_W$) se puede utilizar con die Dichte ($\rho$), der Widerstandskoeffizient ($C_W$), der Gesamtobjektprofil ($S_p$) y die Geschwindigkeit in Bezug auf das Medium ($v$) de acuerdo con la siguiente f rmula:
Die Gesamtwiderstandskraft setzt sich aus den horizontalen Komponenten der Widerstandskraft des Profils des Fl gels $F_W$ und der Auftriebskraft $F_L$ zusammen, die aus dem Anstellwinkel $\alpha$ berechnet werden k nnen:
Aus Messungen geht hervor, dass der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist:
Nach einem bestimmten Winkel nimmt die Kurve ab und erreicht schlie lich den Wert Null. Dies liegt daran, dass ber diesem kritischen Winkel die Wirbel vollst ndig die obere Fl che des Fl gels bedecken und somit der Auftrieb verloren geht. Dieses Ph nomen wird als \"Str mungsabriss\" bezeichnet.
F r kleine Winkel kann die Sinusfunktion durch eine Gerade approximiert werden, die durch den Ursprung verl uft. Wenn der Anstellwinkel eines Flügels ($\alpha$) in Radianten ausgedr ckt wird, ist die Steigung dieser Geraden gleich eins, und wir erhalten:
F r kleine Werte von der Anstellwinkel eines Flügels ($\alpha$) kann die Kosinusfunktion durch eine umgekehrte Parabel approximiert werden, die durch den Ursprung verl uft. Wenn der Winkel in Bogenma ausgedr ckt wird und ungef hr null ist, erhalten wir:
Um die Gesamtwiderstandskraft ($F_R$) zu berechnen, gehen wir von kleinen Winkeln aus und betrachten eine Situation, in der der Winkel so beschaffen ist, dass er die Körpermasse ($m$) beibeh lt. Unter Verwendung dieser Annahme und der Variablen der Koeffizient Fahrstuhl ($C_L$), der Widerstandskoeffizient ($C_W$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Gesamtobjektprofil ($S_p$), die Gravitationsbeschleunigung ($g$), die Proportionalitätskonstante Koeffizient Nachhaltigkeit ($c$), die Dichte ($\rho$) und die Geschwindigkeit in Bezug auf das Medium ($v$) erhalten wir den folgenden Ausdruck:
ID:(464, 0)