Storyboard

Divergence analyzes the flow of the electric field for infinitesimal volumes. This value is proportional to the charge density, so the divergence is a tool to detect the presence of charges since the problem of Gauss's law for larger volumes is that if the sum of the charges cancels out within the volume, then also fields tend to offset.

>Model

ID:(1566, 0)

Image

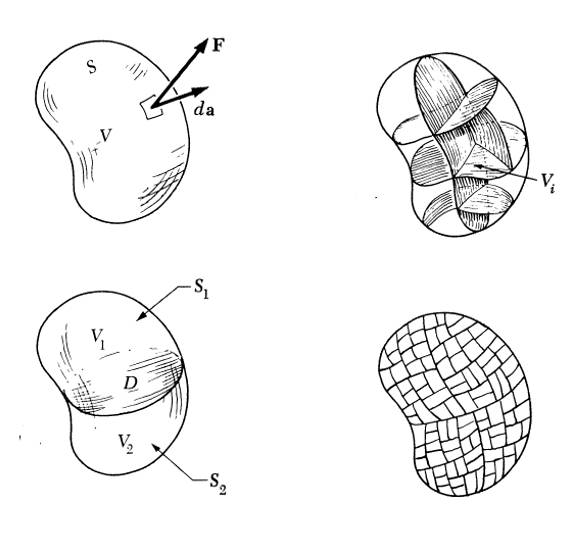
Cuando se analizo el flujo eléctrico se vio que se podia calcular sumando las contribuciones de muchas secciones dS_i mediante

se vio que se podia calcular subdividiendo el volumen en muchas pequeñas superficies dS_i.

En otras palabras un volumen con su respectiva superficie se puede subdividir en múltiples volúmenes con sus correspondientes superficies:

ID:(11560, 0)

Image

Si se toma el flujo del campo eléctrico por el volumen en la dirección \hat{x}:

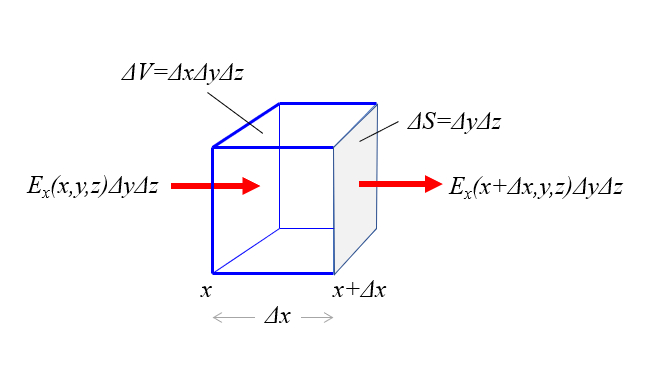
es igual a lo que flujo que saleE_x(x+\Delta x,y,z)\Delta y\Delta zy se resta el flujo que ingresaE_x(x,y,z)\Delta y\Delta zse puede estimar el flujo neto por volumen \Delta x\Delta y\Delta z es\displaystyle\frac{1}{\Delta x\Delta y\Delta z}(E_x(x+\Delta x,y,z)\Delta y\Delta z - E_x(x,y,z)\Delta y\Delta z)=\displaystyle\frac{E_x(x+\Delta x,y,z)-E_x(x,y,z)}{\Delta x}\rightarrow \displaystyle\frac{\partial E_x}{\partial x}

ID:(11616, 0)

Model

Divergence analyzes the flow of the electric field for infinitesimal volumes. This value is proportional to the charge density, so the divergence is a tool to detect the presence of charges since the problem of Gauss's law for larger volumes is that if the sum of the charges cancels out within the volume, then also fields tend to offset.

Variables

$Q$

Q

Charge

C

$\partial/\partial y$

D_y

Derivada parcial en $y$

1/m

$\partial/\partial z$

D_z

Derivada parcial en $z$

1/m

$\epsilon$

epsilon

Dielectric constant

-

$\vec{\nabla}$

div

Divergence

1/m

$E$

E

Electric eield

V/m

$\vec{E}$

&E

Electric field

V/m

$E_x$

E_x

Electric field component in $x$

V/m

$E_y$

E_y

Electric field component in $y$

V/m

$E_z$

E_z

Electric field component in $z$

V/m

$\Phi_i$

Phi_i

Magnetic flux through cell $i$

kg/C s

$\partial/\partial x$

D_x

Partial derivative in $x$

1/m

$S$

S

Surface

m^2

$S_i$

S_i

Surface i

m^2

$V$

V

Volume

m^3

$\rho_e$

rho_e

Volume charge density

C/m^3

$V_i$

V_i

Volume of the $i$th infinitesimal cell

m^3

Calculations

• Alternative method
• Traditional method
• Strategy
• 2D
• 3D

Equation

Number

First, select the equation:   to ,  then, select the variable:   to 

---

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

 Variable   Given   Calculate   Target :   Equation   To be used

Equations

Examples