Druyd:Knowledge

Divergencia del campo

Storyboard

La divergencia analiza el flujo del campo eléctrico para volúmenes infinitesimales. Este valor es proporcional a la densidad de carga con lo que la divergencia es una herramienta para detectar la presencia de cargas ya que el problema de la ley de Gauss para volúmenes mayores es que si la suma de las cargas se anula dentro del volumen entonces también los campo tienden a compensarse.

>Modelo

ID:(1566, 0)

Subdividiendo superficies y volúmenes

Imagen

Cuando se analizo el flujo eléctrico

$ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $

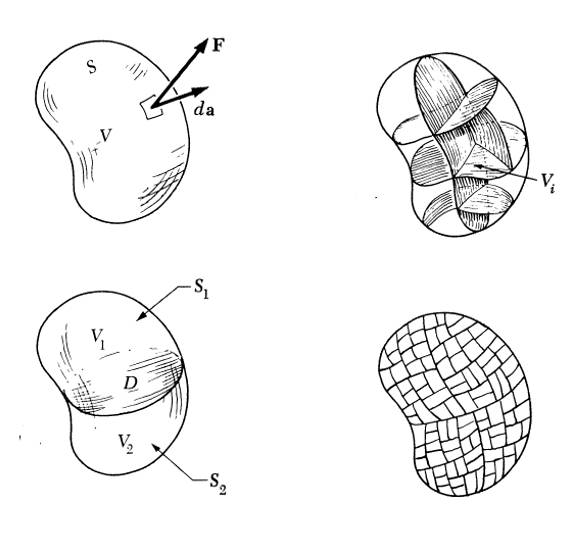
se vio que se podia calcular subdividiendo el volumen en muchas pequeñas superficies dS_i.

En otras palabras un volumen con su respectiva superficie se puede subdividir en múltiples volúmenes con sus correspondientes superficies:

ID:(11560, 0)

Flujo por volumen

Imagen

Si se toma el flujo del campo eléctrico por el volumen en la dirección \hat{x}:

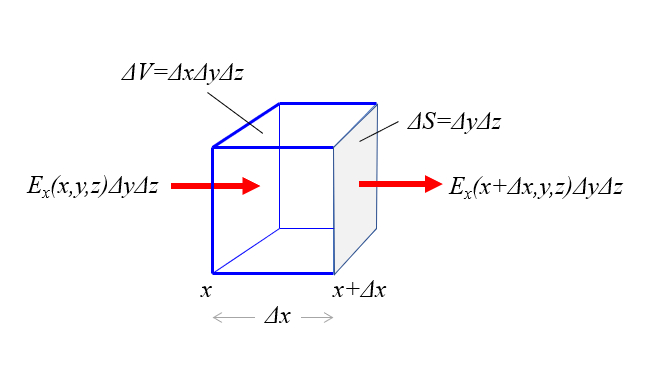
es igual a lo que flujo que saleE_x(x+\Delta x,y,z)\Delta y\Delta zy se resta el flujo que ingresaE_x(x,y,z)\Delta y\Delta zse puede estimar el flujo neto por volumen \Delta x\Delta y\Delta z es\displaystyle\frac{1}{\Delta x\Delta y\Delta z}(E_x(x+\Delta x,y,z)\Delta y\Delta z - E_x(x,y,z)\Delta y\Delta z)=\displaystyle\frac{E_x(x+\Delta x,y,z)-E_x(x,y,z)}{\Delta x}\rightarrow \displaystyle\frac{\partial E_x}{\partial x}

ID:(11616, 0)

Divergencia del campo

Descripción

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$E$

Campo eléctrico

V/m

$\vec{E}$

Campo eléctrico

V/m

$Q$

Carga

$E_x$

E_x

Componente campo eléctrico en $x$

V/m

$E_y$

E_y

Componente campo eléctrico en $y$

V/m

$E_z$

E_z

Componente campo eléctrico en $z$

V/m

$\epsilon$

epsilon

Constante dieléctrica

$\rho_e$

rho_e

Densidad de carga por volumen

C/m^3

$\partial/\partial x$

D_x

Derivada parcial en $x$

1/m

$\partial/\partial y$

D_y

Derivada parcial en $y$

1/m

$\partial/\partial z$

D_z

Derivada parcial en $z$

1/m

$\vec{\nabla}$

div

Divergencia

1/m

$\Phi_i$

Phi_i

Flujo magnético por la celda $i$

kg/C s

$S$

Superficie

m^2

$S_i$

S_i

Superficie i

m^2

$V$

Volumen

m^3

$V_i$

V_i

Volumen de la $i$ esima celda infinitesimal

m^3

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$\Phi_i = \displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$

Phi_i = @INT( &E . d&S_i , S_i )

(ID 11561)

$\nabla\cdot\vec{E} = \lim_{V_i\rightarrow 0} \displaystyle\frac{1}{V_i}\displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$

nabla . &E = @LIM( (1/ V_i )*@INT( &E . d&S_i , S_i ), V_i , 0)

(ID 11562)

$\displaystyle\int_S \vec{E}\cdot d\vec{S} = \displaystyle\int_V (\nabla\cdot\vec{E}) dV$

(ID 11563)

$ Q = \displaystyle\int_V \rho dV$

Q =@INT( V * rho , V )

(ID 11564)

$\nabla\cdot\vec{E} = \displaystyle\frac{\rho}{\epsilon_0\epsilon}$

nabla . &E = rho /( epsilon_0 * epsilon )

(ID 11565)

$ \nabla\cdot\vec{E} = \displaystyle\frac{\partial E_x}{\partial x}+ \displaystyle\frac{\partial E_y}{\partial y}+ \displaystyle\frac{\partial E_z}{\partial z}$

nabla . &E = dE_x / dx + dE_y / dy + dE_z / dz

(ID 11566)

Ejemplos

Subdividiendo superficies y vol menes

Cuando se analizo el flujo el ctrico

$ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $

se vio que se podia calcular subdividiendo el volumen en muchas peque as superficies dS_i.

En otras palabras un volumen con su respectiva superficie se puede subdividir en m ltiples vol menes con sus correspondientes superficies:

(ID 11560)

Flujo por volumen

Si se toma el flujo del campo el ctrico por el volumen en la direcci n \hat{x}:

(ID 11616)

ID:(1566, 0)