Benützer:


Felddivergenz
Storyboard

Die Divergenz analysiert den Fluss des elektrischen Feldes auf infinitesimale Volumina. Dieser Wert ist proportional zur Ladungsdichte, daher ist die Divergenz ein Werkzeug zum Erkennen des Vorhandenseins von Ladungen, da das Problem des Gaußschen Gesetzes für größere Volumina darin besteht, dass, wenn sich die Summe der Ladungen innerhalb des Volumens aufhebt, auch Felder neigen dazu, sich zu versetzen.

>Modell

ID:(1566, 0)


Unterteilung von Flächen und Volumen
Definition

Cuando se analizo el flujo eléctrico se vio que se podia calcular sumando las contribuciones de muchas secciones dS_i mediante

$ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $



se vio que se podia calcular subdividiendo el volumen en muchas pequeñas superficies dS_i.

En otras palabras un volumen con su respectiva superficie se puede subdividir en múltiples volúmenes con sus correspondientes superficies:

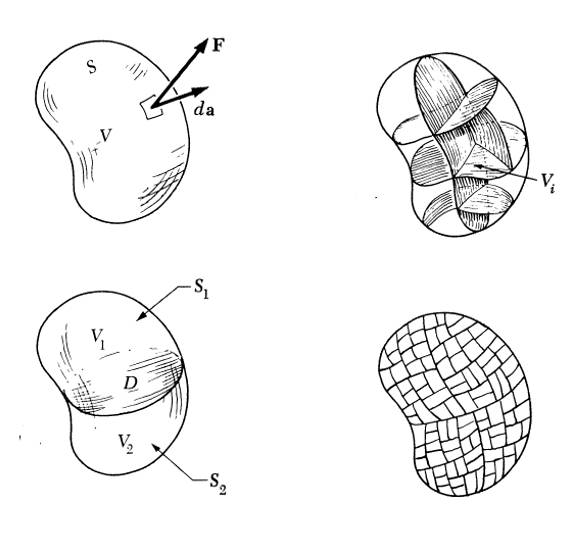
ID:(11560, 0)


Flow by volume
Bild

Si se toma el flujo del campo eléctrico por el volumen en la dirección \hat{x}:

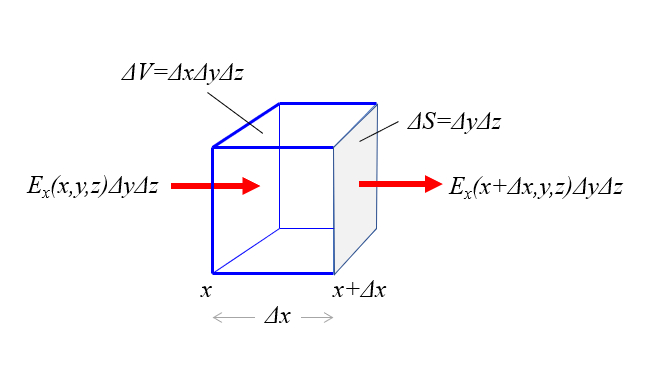
es igual a lo que flujo que sale

E_x(x+\Delta x,y,z)\Delta y\Delta z

y se resta el flujo que ingresa

E_x(x,y,z)\Delta y\Delta z

se puede estimar el flujo neto por volumen \Delta x\Delta y\Delta z es

\displaystyle\frac{1}{\Delta x\Delta y\Delta z}(E_x(x+\Delta x,y,z)\Delta y\Delta z - E_x(x,y,z)\Delta y\Delta z)=\displaystyle\frac{E_x(x+\Delta x,y,z)-E_x(x,y,z)}{\Delta x}\rightarrow \displaystyle\frac{\partial E_x}{\partial x}

ID:(11616, 0)


Felddivergenz
Beschreibung

Die Divergenz analysiert den Fluss des elektrischen Feldes auf infinitesimale Volumina. Dieser Wert ist proportional zur Ladungsdichte, daher ist die Divergenz ein Werkzeug zum Erkennen des Vorhandenseins von Ladungen, da das Problem des Gaußschen Gesetzes für größere Volumina darin besteht, dass, wenn sich die Summe der Ladungen innerhalb des Volumens aufhebt, auch Felder neigen dazu, sich zu versetzen.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\partial/\partial y$
D_y
Derivada parcial en $y$
1/m
$\partial/\partial z$
D_z
Derivada parcial en $z$
1/m
$\epsilon$
epsilon
Dielektrizitätskonstante
-
$\vec{\nabla}$
div
Divergenz
1/m
$E_x$
E_x
Elektrische Feldkomponente in $x$
V/m
$E_y$
E_y
Elektrische Feldkomponente in $y$
V/m
$E_z$
E_z
Elektrische Feldkomponente in $z$
V/m
$\vec{E}$
&E
Elektrisches Feld
V/m
$E$
E
Elektrisches Feld
V/m
$Q$
Q
Ladung
C
$\Phi_i$
Phi_i
Magnetischer Fluss durch die Zelle $i$
kg/C s
$S$
S
Oberfläche
m^2
$S_i$
S_i
Oberfläche i
m^2
$\partial/\partial x$
D_x
Partielle Ableitung in $x$
1/m
$V$
V
Volumen
m^3
$V_i$
V_i
Volumen der $i$ten Infinitesimalzelle
m^3
$\rho_e$
rho_e
Volumenladungsdichte
C/m^3

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Beispiele

Cuando se analizo el flujo el ctrico se vio que se podia calcular sumando las contribuciones de muchas secciones dS_i mediante

$ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $



se vio que se podia calcular subdividiendo el volumen en muchas peque as superficies dS_i.

En otras palabras un volumen con su respectiva superficie se puede subdividir en m ltiples vol menes con sus correspondientes superficies:

(ID 11560)

Al subdividir el volumen en peque os vol menes infinitesimales V_i con una superficie en su entorno S_i se puede calcular la contribuci n al flujo

$\Phi_i = \displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$

(ID 11561)

Si se toma el flujo del campo el ctrico por el volumen en la direcci n \hat{x}:

es igual a lo que flujo que sale

E_x(x+\Delta x,y,z)\Delta y\Delta z

y se resta el flujo que ingresa

E_x(x,y,z)\Delta y\Delta z

se puede estimar el flujo neto por volumen \Delta x\Delta y\Delta z es

\displaystyle\frac{1}{\Delta x\Delta y\Delta z}(E_x(x+\Delta x,y,z)\Delta y\Delta z - E_x(x,y,z)\Delta y\Delta z)=\displaystyle\frac{E_x(x+\Delta x,y,z)-E_x(x,y,z)}{\Delta x}\rightarrow \displaystyle\frac{\partial E_x}{\partial x}

(ID 11616)

El flujo en la direcci n \hat{x} es

\displaystyle\frac{\partial E_x}{\partial x}

por lo que el flujo total se puede generalizar a tres dimensiones que corresponde de hecho al producto punto del vector derivada

\vec{
abla} = \hat{x}\displaystyle\frac{\partial }{\partial x}+\hat{y}\displaystyle\frac{\partial }{\partial y}+\hat{z}\displaystyle\frac{\partial }{\partial z}

con lo que la divergencia se define como:

$ \nabla\cdot\vec{E} = \displaystyle\frac{\partial E_x}{\partial x}+ \displaystyle\frac{\partial E_y}{\partial y}+ \displaystyle\frac{\partial E_z}{\partial z}$

(ID 11566)

Como el volumen V_i es infinitesimalmente chico tambi n lo ser su superficie S_i. Sin embargo se puede definir el flujo por volumen que al ser ambas magnitudes infinitesimal puede no ser nulo. Esta proporci n la denominamos la divergencia y se define como

$\nabla\cdot\vec{E} = \lim_{V_i\rightarrow 0} \displaystyle\frac{1}{V_i}\displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$

(ID 11562)

Si consideramos el flujo segmentado

\displaystyle\int_S \vec{E}\cdot d\vec{S}=\displaystyle\sum_i \displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i

se puede empleamos la definici n de la divergencia

$\nabla\cdot\vec{E} = \lim_{V_i\rightarrow 0} \displaystyle\frac{1}{V_i}\displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$



para pasar de la suma de suma de volumenes

\displaystyle\int_S \vec{E}\cdot d\vec{S}=\displaystyle\sum_i V_i \vec{
abla}\cdot\vec{E}\rightarrow \displaystyle\int_V (\vec{
abla}\cdot\vec{E})dV

a la integral del volumen

$\displaystyle\int_S \vec{E}\cdot d\vec{S} = \displaystyle\int_V (\nabla\cdot\vec{E}) dV$

(ID 11563)

En la ley de Gauss se tenia una carga Q rodeada en una superficie S (la superficie gaussiana). Con ello tiene sentido de hablar de una densidad de carga \rho como la carga por unidad de volumen asociado a la superficie. Con ello la carga Q es la integral de la densidad de carga en el volumen

$ Q = \displaystyle\int_V \rho dV$

(ID 11564)

Si comparamos la ley de Gauss

$\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$



con el teorema de la divergencia

$\displaystyle\int_S \vec{E}\cdot d\vec{S} = \displaystyle\int_V (\nabla\cdot\vec{E}) dV$



y la definici n de la densidad de carga

$ Q = \displaystyle\int_V \rho dV$



se obtiene la ley diferencial de Gauss

$\nabla\cdot\vec{E} = \displaystyle\frac{\rho}{\epsilon_0\epsilon}$



La ley de Gauss en su forma diferencial 'detecta' las cargas en los vol menes infinitesimales obviando el problema que en el teorema de Gauss integral en que para vol menes mayores si la suma de las cargas contenidas se anula el campo tambi n se compensa.

(ID 11565)

ID:(1566, 0)