User:


Electric field rotor
Storyboard

The electric field rotor seeks to detect if there is circulation in it. Circulation would mean that closed field lines existed, that without existing charges in space they close on themselves. A particle in that field would make a closed path without escaping or falling on or to any load. For the static case it is shown that there is no such circulation and that all field lines start and end in loads.

>Model

ID:(1569, 0)


Circulation
Definition

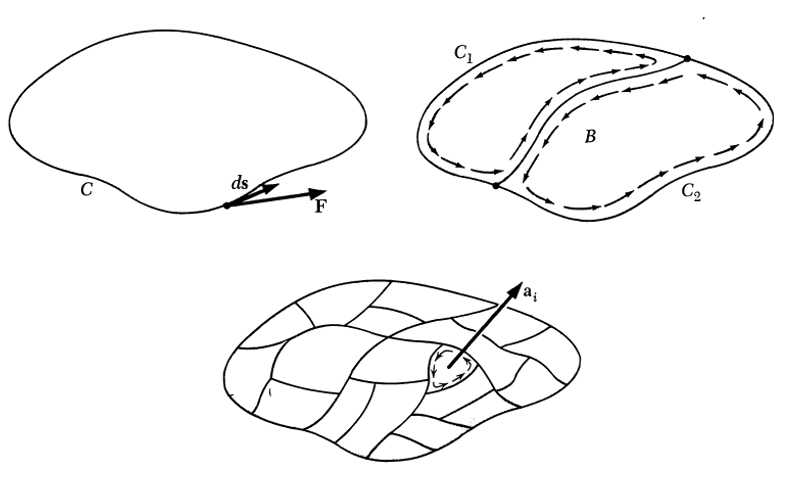
Cuando se estableció el potencial eléctrico se trabajo con la idea de caminos entre dos puntos que en el caso de ser serrados eran nulos:

$ \Delta\varphi = -\displaystyle\int_C \vec{E}\cdot d\vec{s} $



Dichos caminos se pueden segmentar en caminos mas pequeños:

ID:(11569, 0)


Electric field rotor
Description

The electric field rotor seeks to detect if there is circulation in it. Circulation would mean that closed field lines existed, that without existing charges in space they close on themselves. A particle in that field would make a closed path without escaping or falling on or to any load. For the static case it is shown that there is no such circulation and that all field lines start and end in loads.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$\vec{\nabla}$
div
Divergence
1/m
$E$
E
Electric eield
V/m
$\vec{E}$
&E
Electric field
V/m
$\Gamma$
Gamma
Electric field circulation
V
$d\vec{s}$
d&s
Length element (vector)
m
$d\vec{s}_i$
d&s_i
Long element around cell $i$
m
$rot$
rot
Rotor
1/m
$dS$
dS
Surface element
m^2
$S_i$
S_i
Surface i
m^2
$\hat{n}_i$
&n_i
Versor normal to surface i
-

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Examples

Cuando se estableci el potencial el ctrico se trabajo con la idea de caminos entre dos puntos que en el caso de ser serrados eran nulos:

$ \Delta\varphi = -\displaystyle\int_C \vec{E}\cdot d\vec{s} $



Dichos caminos se pueden segmentar en caminos mas peque os:

(ID 11569)

En base al integral a lo largo de un camino se puede definir la circulaci n como

$ \Gamma = \displaystyle\int_C \vec{E}\cdot d\vec{s}$

(ID 11570)

Una circulaci n general

$ \Gamma = \displaystyle\int_C \vec{E}\cdot d\vec{s}$



puede ser descompuesta en circulaciones menores

$\displaystyle\int_C \vec{E}\cdot d\vec{s} = \displaystyle\sum_i \displaystyle\int_{C_i} \vec{E}\cdot d\vec{s}_i$

(ID 11571)

An logo a la definici n de la divergencia

$\nabla\cdot\vec{E} = \lim_{V_i\rightarrow 0} \displaystyle\frac{1}{V_i}\displaystyle\int_{S_i} \vec{E}\cdot d\vec{S}_i$



se puede definir como el rotor la circulaci n por rea en la direcci n de la normal a la superficie

$ (\nabla\times\vec{E})\cdot\hat{n} = \lim_{S_i\rightarrow 0}\displaystyle\frac{1}{ S_i }\displaystyle\int_{C_i}\vec{E}\cdot d\vec{s}$

(ID 11572)

Con la definici n del rotor

$ (\nabla\times\vec{E})\cdot\hat{n} = \lim_{S_i\rightarrow 0}\displaystyle\frac{1}{ S_i }\displaystyle\int_{C_i}\vec{E}\cdot d\vec{s}$



se tiene que la suma sobre las superficies es

\displaystyle\int_C\vec{E}\cdot d\vec{s}=\displaystyle\sum_i S_i(
abla\times\vec{E})\cdot d\vec{S}=\displaystyle\int_S (
abla\times\vec{E})\cdot d\vec{S}

que corresponde al teorema de Stokes

$ \displaystyle\int_C \vec{E} \cdot d\vec{s} =\displaystyle\int_S (\nabla\times\vec{E} )\cdot d\vec{S} $

(ID 11573)

As the circulation on a closed road is null

$ \displaystyle\oint_C \vec{E}\cdot d\vec{s}=0$



Stokes' theorem

$ \displaystyle\int_C \vec{E} \cdot d\vec{s} =\displaystyle\int_S (\nabla\times\vec{E} )\cdot d\vec{S} $



implies that

$ \nabla\times\vec{E} = 0 $



This means that in the case of electrostatics the electric field has no circulation, that is, its lines do not form closed circles without touching charges.

(ID 11574)

ID:(1569, 0)