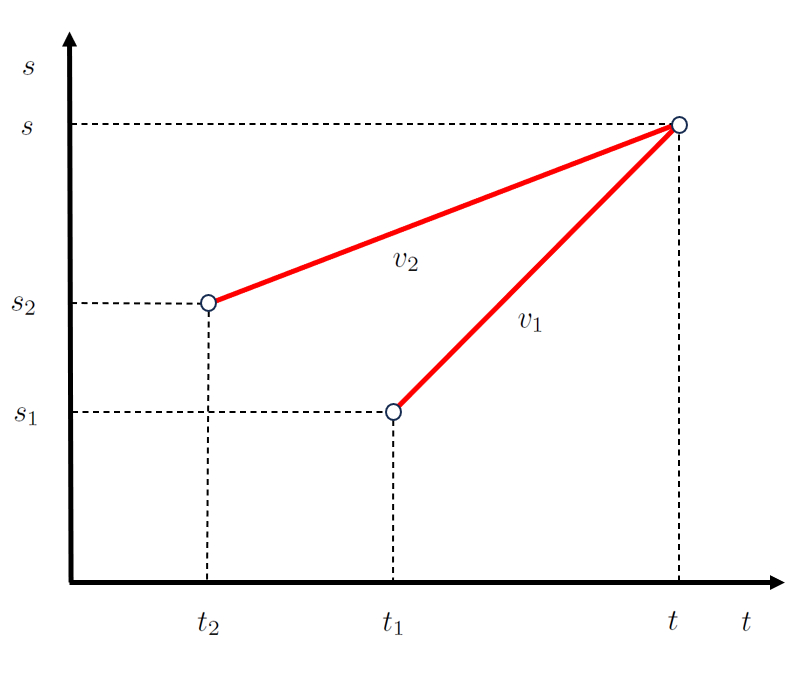
Durant le processus d'intersection, deux corps se d placent de mani re co ncider en a position de l'intersection ($s$) et le temps d'intersection ($t$).

Pour cela, chaque corps doit partir de ses positions et temps initiaux, avec des d placements respectifs de a vitesse du premier étage ($v_1$) et a vitesse du premier étage ($v_1$), de sorte que la co ncidence se produise.

mechanisms

Dans le cas de l'interception, deux corps se d placent de mani re se rencontrer en un temps d'intersection ($t$) dans leur ERROR:10258,0.

cet effet, chaque corps :

• Commence le heure initiale du premier objet ($t_1$) avec a position initiale du premier objet ($s_1$) comme sa position initiale et a vitesse du premier étage ($v_1$) comme son d placement.
• Commence le temps initial du deuxième objet ($t_2$) avec a position initiale du deuxième objet ($s_2$) comme sa position initiale et a vitesse du deuxième étage ($v_2$) comme son d placement.

Ces conditions doivent tre remplies pour que l'interception se produise.

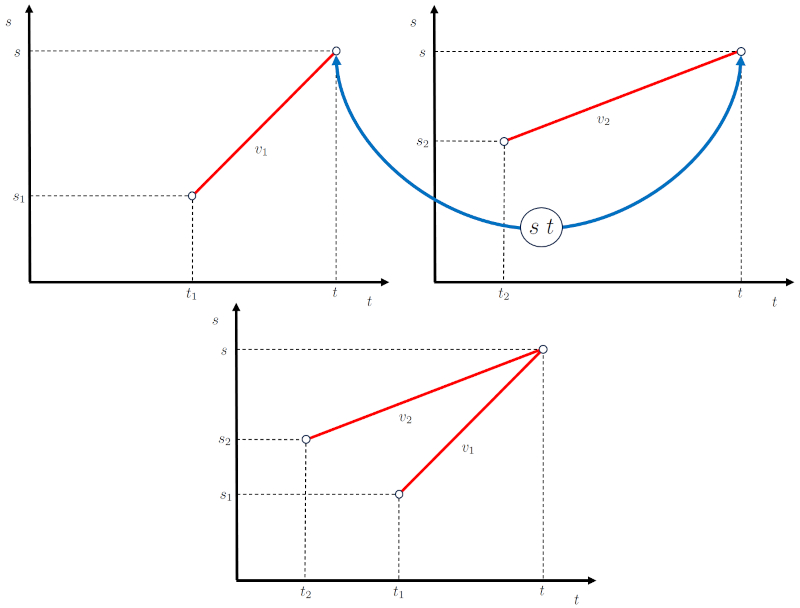
Ainsi, les diagrammes de position dans le temps peuvent tre coupl s comme indiqu dans la repr sentation suivante :

image

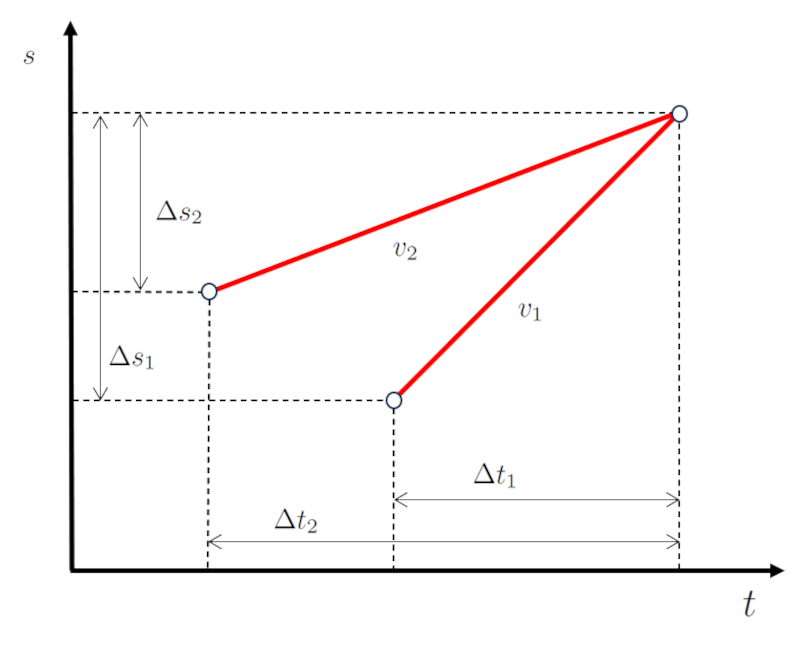
Dans le cas d'une intersection ou d'une collision entre deux objets, il est courant que a vitesse du premier étage ($v_1$) et a vitesse du deuxième étage ($v_2$) doivent tre tels qu'une concordance se produise.

Cela signifie que a distance parcourue par le premier objet ($\Delta s_1$) et a temps de trajet du premier objet ($\Delta t_1$) doivent aboutir une vitesse de une vitesse du premier étage ($v_1$),

equation=3152,1

de sorte qu'avec a distance parcourue par le deuxième objet ($\Delta s_2$) et a temps de trajet du deuxième objet ($\Delta t_2$), nous obtenons une vitesse du deuxième étage ($v_2$),

equation=3152,2

pour qu'ils finissent par co ncider en temps et en espace (position) :

image

Dans le cas d'un mouvement o deux objets s'interceptent, tels que a position de l'intersection ($s$) et le temps d'intersection ($t$), cela est commun chacun d'eux. Ainsi, si pour le premier objet le heure initiale du premier objet ($t_1$) et a position initiale du premier objet ($s_1$) avec a vitesse du premier étage ($v_1$) sont respect s :

equation=3154,1

et pour le deuxi me objet le temps initial du deuxième objet ($t_2$) et a position initiale du deuxième objet ($s_2$) avec a vitesse du deuxième étage ($v_2$) sont respect s :

equation=3154,2

ce qui est repr sent comme suit :

image

La cl est que les deux objets se rencontrent en a position de l'intersection ($s$) un moment le temps d'intersection ($t$). Pour ce faire, l'objet 1 commence son voyage en a position initiale du premier objet ($s_1$) Un heure initiale du premier objet ($t_1$) avec une vitesse du premier étage ($v_1$), tandis que l'objet 2 commence son voyage en a position initiale du deuxième objet ($s_2$) Un temps initial du deuxième objet ($t_2$) avec une vitesse du deuxième étage ($v_2$). Au cours de ce processus, l'objet 1 parcourt une distance parcourue par le premier objet ($\Delta s_1$) Une temps de trajet du premier objet ($\Delta t_1$), tandis que l'objet 2 parcourt une distance parcourue par le deuxième objet ($\Delta s_2$) Une temps de trajet du deuxième objet ($\Delta t_2$) :

model

Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) partir de a vitesse ($s_0$) et a position ($s$) gr ce l' quation suivante :

kyon

Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) partir de a vitesse ($s_0$) et a position ($s$) gr ce l' quation suivante :

kyon

Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :

kyon

Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :

kyon

A vitesse moyenne ($\bar{v}$) peut tre calcul partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisantxa0:

kyon

A vitesse moyenne ($\bar{v}$) peut tre calcul partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisantxa0:

kyon

Si la vitesse est constante, la vitesse sera gale a vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut tre calcul e en utilisant la diff rence entre a position ($s$) et a vitesse ($s_0$), divis e par la diff rence entre le temps ($t$) et le temps initial ($t_0$) :

kyon

L' quation correspondante d finit une ligne droite dans l'espace-temps.

Si la vitesse est constante, la vitesse sera gale a vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut tre calcul e en utilisant la diff rence entre a position ($s$) et a vitesse ($s_0$), divis e par la diff rence entre le temps ($t$) et le temps initial ($t_0$) :

kyon

L' quation correspondante d finit une ligne droite dans l'espace-temps.