Lorsquun objet se d place vitesse constante, il parcourt des distances gales pendant des intervalles de temps gaux. Dans ce cas, la position varie lin airement avec le temps coul .

Pour comprendre ce mod le, lancez la simulation avec le bouton Start et arr tez-la avec Stop. Ensuite, observez les valeurs indiqu es sur la r gle inf rieure : a distance parcourue en un temps ($\Delta s$), et sur le chronom tre : le temps écoulé ($\Delta t$). En divisant la premi re par la seconde, vous obtenez la vitesse saisie : a vitesse constante ($v_0$).

simulation

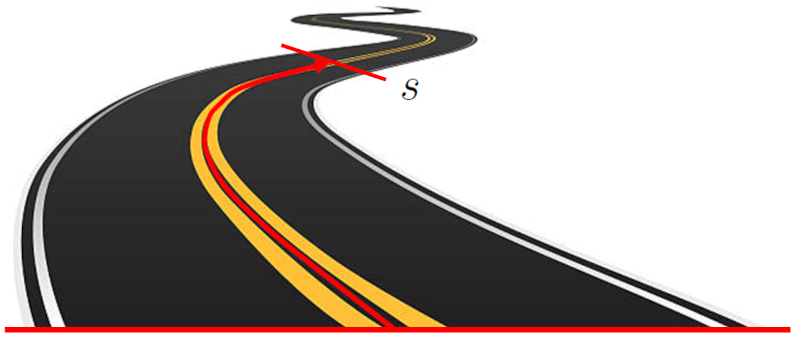
A position ($s$) d'un objet dans un syst me unidimensionnel fait r f rence l'emplacement de l'objet par rapport un point de r f rence. Cette position est exprim e comme la distance entre l\'objet et le point d\'origine. Cette distance peut tre une ligne droite sur un axe cart sien, ou elle peut suivre un chemin courbe.

image

Position le long d'une route suivant son axe

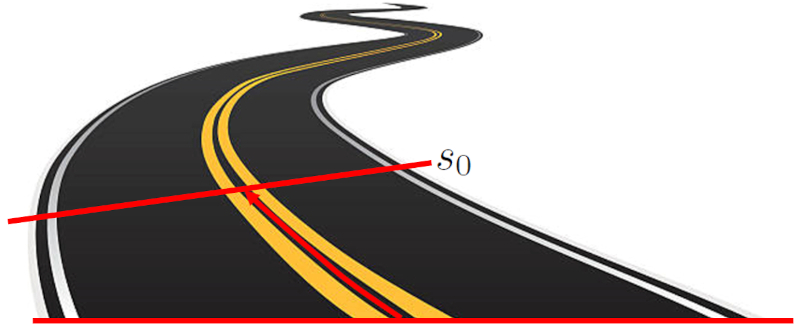
A vitesse ($s_0$) est l'emplacement de d part d'un objet avant que tout mouvement ne commence. Cette position est d finie comme la distance entre l'objet et le point d\'origine. Cette distance peut tre une ligne droite sur un axe cart sien ou elle peut suivre une trajectoire courbe.

image

Position initiale le long d'une route suivant son axe

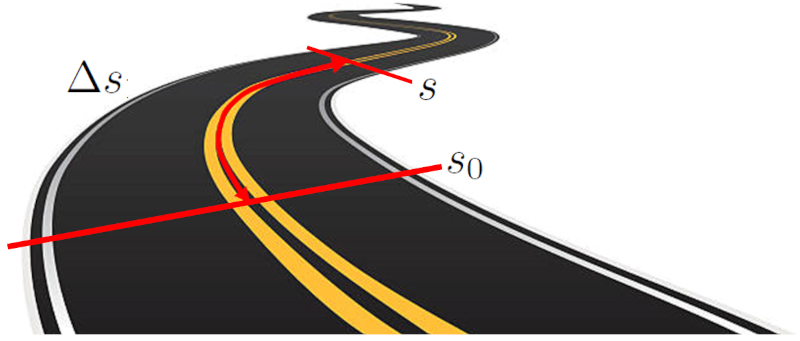
A distance parcourue en un temps ($\Delta s$) pour un objet est d termin en mesurant la distance entre deux points sp cifiques le long d'un trajet. Ce trajet peut tre une ligne droite dans un rep re cart sien ou une trajectoire courbe. La distance est calcul e comme la longueur du chemin reliant les points de d part et d'arriv e.

image

Distance parcourue dun point initial un point final

Comme la valeur de a distance parcourue en un temps ($\Delta s$) est calcul e comme la diff rence entre a position ($s$) et a vitesse ($s_0$) :

equation=4352

il est possible de d placer lorigine de la position en ajoutant une valeur constante $d$ aux deux grandeurs :

$s \rightarrow s + d$

$s_0 \rightarrow s_0 + d$

sans affecter le r sultat de la distance parcourue :

$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$

Ce concept est appel invariance spatiale, ce qui signifie que la valeur de la distance parcourue ne d pend pas du point sp cifique o commence la mesure.

Cela implique que les lois formul es en utilisant ce principe seront invariantes spatiales, cest- -dire quelles resteront valides quel que soit lendroit o la mesure est effectu e.

L' volution de tout syst me est d crite par diff rents param tres, chacun voluant selon une chelle appel e le temps ($t$).

image

Heure indiqu e par une horloge, soit la valeur laquelle elle marque, soit l'heure

Traditionnellement, le temps tait consid r comme absolu dans la physique classique, tant le m me dans tous les syst mes de r f rence. Cependant, la th orie de la relativit a g n ralis ce concept et doit maintenant tre consid r comme unique pour chaque syst me de r f rence, pouvant diff rer dans son avancement.

Les syst mes sont invariants dans le temps, ce qui signifie que leur comportement n'est pas affect par le moment o le processus commence. Cela nous permet de choisir le temps initial ($t_0$), en fonction de ce qui est le plus pratique. Cela pourrait tre bas sur l'instrument utilis pour mesurer le temps ou pour faciliter les calculs.

image

L'heure laquelle commence la mesure, qu'elle soit fixe ou par syst me (chronom tre)

Au final, le moment de d part peut tre choisi librement.

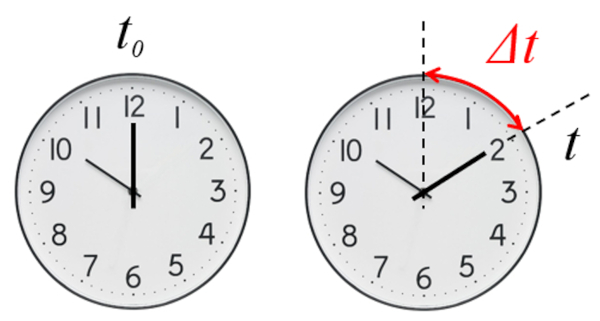
La base de la description de toute volution est la d finition du temps auquel elle est d crite. En particulier, on travaille avec le temps écoulé ($\Delta t$) depuis un temps de r f rence.

image

Le chronom tre nous indique directement le temps coul puisque son temps initial est z ro

Dans le cas d'un chronom tre, le temps coul est mesur depuis le d but de sa mesure, c'est- -dire un temps initial nul ($t_0=0$).

image

Dans le cas de l'horloge, il est n cessaire de d finir le type initial afin de d terminer le temps coul .

Dans le cas d'une montre, le temps coul est mesur depuis un temps initial d fini, qui peut tre nul ou non.

Comme le temps écoulé ($\Delta t$) est calcul comme la diff rence entre le temps ($t$) et le temps initial ($t_0$) :

equation=4353

il est possible de d placer lorigine du temps en ajoutant une valeur constante

aux deux magnitudes :

$t \rightarrow t + \tau$

$t_0 \rightarrow t_0 + \tau$

sans affecter le r sultat du temps coul :

$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$

Ce concept est appel invariance temporelle, ce qui signifie que la valeur du temps coul ne d pend pas du moment pr cis o commence la mesure.

Cela implique que les lois formul es en utilisant ce principe seront invariantes dans le temps, cest- -dire quelles resteront valides quelles soient appliqu es dans le pr sent, le pass ou le futur.

Pour pouvoir estimer le d placement d'un objet, nous devons conna tre la distance parcourue par unit de temps qu'il parcourt. C'est pourquoi on introduit la proportion entre la distance parcourue et le temps coul , appel e la vitesse moyenne.

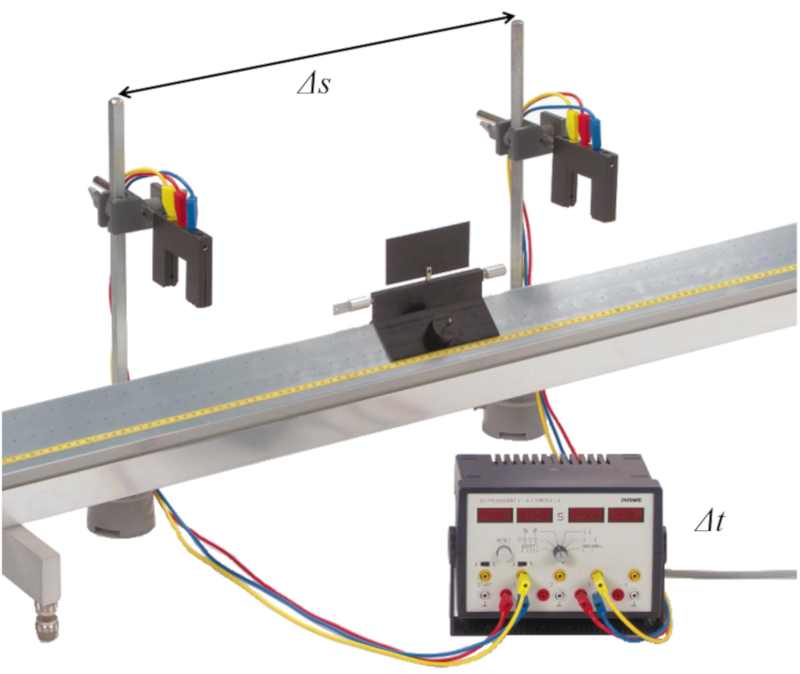
Pour effectuer la mesure, on peut travailler avec un syst me comme celui pr sent dans l'image :

image

Pour d terminer la vitesse moyenne, il faut placer deux capteurs qui enregistrent le passage d'un objet une distance $\Delta s$. Ensuite, on enregistre la diff rence de temps laquelle l\'objet passe devant chaque capteur $\Delta t$. Les deux valeurs permettent de d terminer la vitesse moyenne en divisant la distance parcourue par le temps coul .

L' quation qui d crit a vitesse moyenne ($\bar{v}$) avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) est la suivantexa0:

equation=3152

Il convient de rappeler que la vitesse moyenne est une estimation de la vitesse r elle. Le principal probl me r side dans le fait que :

Si la vitesse varie au cours du temps coul , la valeur de la vitesse moyenne peut tre tr s diff rente d\'une vitesse moyenne r elle.

De plus, il y a un probl me dans la fa on dont on mesure la distance parcourue, car on travaille avec deux positions. Cela peut conduire ce que

Comme la distance parcourue est calcul e partir de la diff rence entre deux positions, il peut arriver que, si le mouvement s\'inverse pendant le temps coul , la position initiale et finale soient tr s similaires. Cela peut conduire une vitesse moyenne approximativement nulle, bien que l\'on ait parcouru une distance \\\\\"longue\\\\\".

C\'est pourquoi la cl est de

D terminer la vitesse un moment suffisamment court pour que sa variation soit minimale.

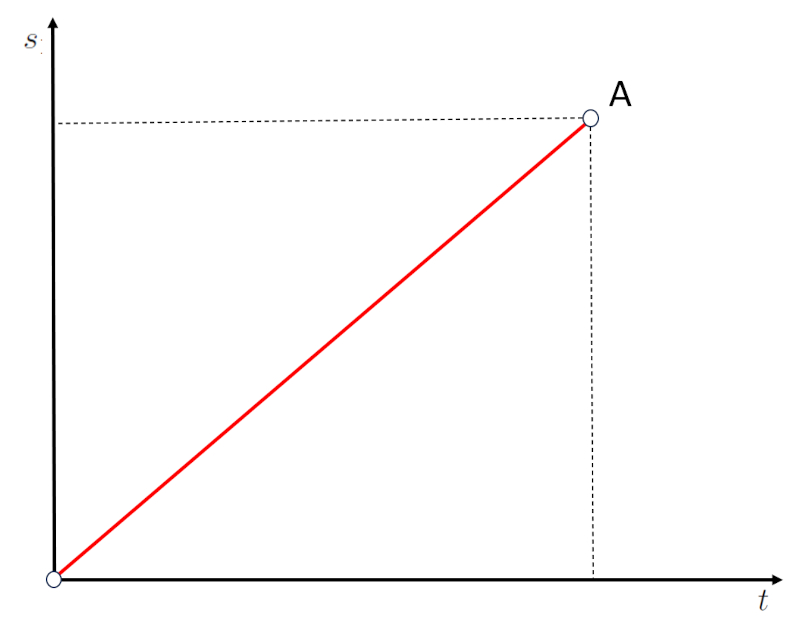
Si le d placement est repr sent graphiquement sous forme d\'une ligne entre l\'origine O et le point A :

image

il est possible de voir qu\'un trajet a t parcouru sur une p riode de temps. Par cons quent, la pente du graphe repr sentant le trajet en fonction du temps coul correspond la vitesse.

Si la pente est plus raide, cela signifie qu\'un trajet est parcouru en moins de temps, ce qui correspond une vitesse plus lev e.

Si la pente est plus plate, cela signifie qu\'un trajet est parcouru en plus de temps, ce qui correspond une vitesse plus faible.

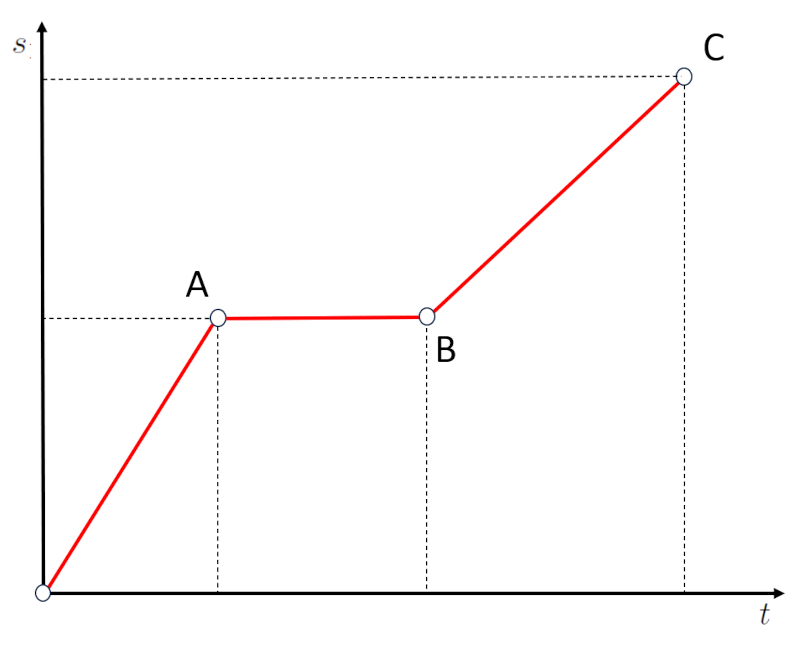
Un deuxi me type de cas concerne les segments horizontaux sur le graphique du parcours par rapport au temps :

image

Si nous observons le segment AB, nous remarquerons que m me si du temps s\'est coul , le parcours n\'a pas chang . Cela signifie que l\'objet est l\'arr t. Ainsi, les segments horizontaux, qui correspondent une pente nulle, correspondent des tapes o la vitesse est nulle.

Pour le cas d'une vitesse constante et d'un temps initial, la position peut tre calcul e en utilisant les valeurs a position ($s$), a vitesse ($s_0$), a vitesse constante ($v_0$), le temps ($t$) et le temps initial ($t_0$) avec l' quation suivante :

equation=3154

qui correspond une ligne droite avec :

• une pente gale a vitesse constante ($v_0$)
• une intersection sur l'axe des ordonn es a vitesse ($s_0$) pour le temps initial ($t_0$)

comme illustr ci-dessous :

image

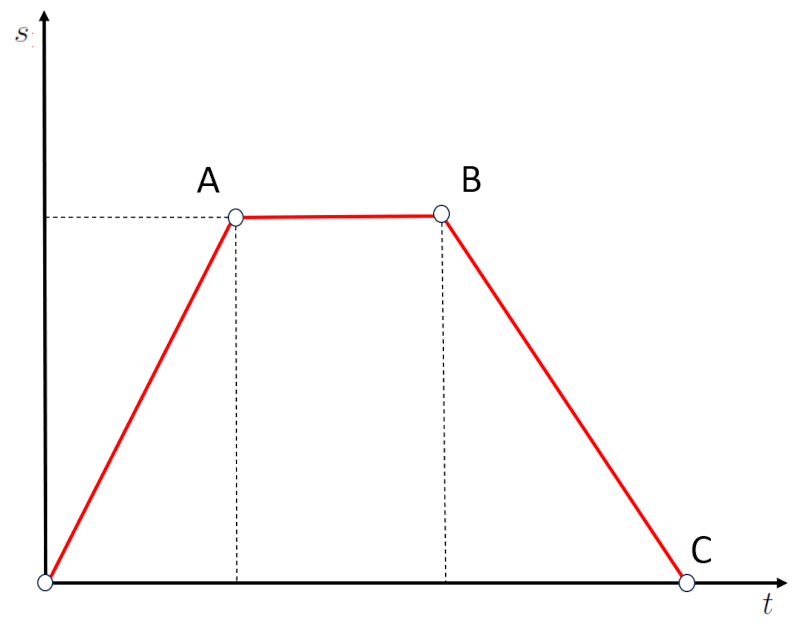
Le cas d\'une pente n gative sur un graphique est le suivant :

image

Cela correspond une situation o l\'objet est revenu de la position B la position C, qui est une distance nulle. En d\'autres termes, les pentes n gatives correspondent un d placement dans la direction oppos e, rapprochant l\'objet de l\'origine plut t que l\' loignant.

Si un corps est "au repos", cela signifie qu\'il est au repos par rapport notre syst me de r f rence ou syst me de coordonn es. Cependant, ce "repos" est totalement relatif, c\'est- -dire que pour un corps qui se d place par rapport notre syst me, le corps "au repos" est galement en mouvement.

En ce sens, il n\'y a pas de "corps au repos" comme quelque chose d\'absolu, il existe comme quelque chose de relatif par rapport un syst me de r f rence particulier. C\'est pourquoi toute mesure de vitesse est g n ralement une mesure par rapport un syst me de r f rence particulier.

Par exemple, si un corps semble se d placer tr s lentement, cela signifie simplement que sa vitesse est tr s similaire la vitesse du syst me de r f rence dans lequel le mouvement lent est observ .

Le mod le de base relie a position ($s$), mesur partir d'un origine a vitesse ($s_0$), r sultant en une distance parcourue en un temps ($\Delta s$), et le temps ($t$), mesur partir d'une origine le temps initial ($t_0$), r sultant en le temps écoulé ($\Delta t$). partir de ces diff rences, a vitesse moyenne ($\bar{v}$) est d fini, qui, s'il est suppos constant, est gal a vitesse constante ($v_0$).

La relation de base du mod le est la droite qui associe les variables centrales du mod le :

image=2243

Avec cela, la structure en r seau du mod le est :

model

Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) partir de a vitesse ($s_0$) et a position ($s$) gr ce l' quation suivante :

kyon

Pour d crire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La dur e est d termin e en soustrayant le temps initial du temps final :

kyon

A vitesse moyenne ($\bar{v}$) peut tre calcul partir de a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$) en utilisantxa0:

kyon

Si la vitesse est constante, la vitesse sera gale a vitesse initiale ($v_0$). Dans ce cas, la distance parcourue en fonction du temps peut tre calcul e en utilisant la diff rence entre a position ($s$) et a vitesse ($s_0$), divis e par la diff rence entre le temps ($t$) et le temps initial ($t_0$) :

kyon

L' quation correspondante d finit une ligne droite dans l'espace-temps.