Storyboard

La vitesse moyenne est définie en considérant la distance parcourue sur un intervalle de temps écoulé, sans prendre en compte les éventuelles fluctuations de vitesse.

Pour déterminer la vitesse à un instant spécifique, il est nécessaire de considérer un intervalle de temps infinitésimalement petit de manière à ce que la vitesse reste presque constante à l'intérieur de cet intervalle.

Cela conduit au calcul de la vitesse instantanée en calculant la vitesse moyenne dans la limite lorsque l'intervalle de temps tend vers zéro. Mathématiquement, cela correspond à la dérivée de la position par rapport au temps et représente la pente de la courbe position-temps.

>Modèle

ID:(1432, 0)

Définition

D'une part, il est important de différencier entre le cas le plus simple, unidimensionnel, et celui plus complexe impliquant plus d'une dimension. Dans les deux cas, la dérivée de a position ($s$) par rapport à Le temps ($t$), qui correspond à la pente de la courbe de a position ($s$), est égale à A vitesse ($v$). De même, la dérivée de a position (vector) ($\vec{s}$) par rapport à Le temps ($t$) correspond à A vitesse (vector) ($\vec{v}$).

D'autre part, la zone sous la courbe de a vitesse ($v$) à Le temps ($t$), correspondant à l'intégration, nous permet de calculer a position ($s$).

ID:(15393, 0)

Image

A vitesse ($v$) est défini comme le déplacement par unité de temps. Cependant, ce concept se réduit à Une vitesse moyenne ($\bar{v}$) qui existe pendant l'intervalle de temps considéré.

La limitation de la vitesse moyenne est reflétée dans le fait qu'on suppose qu'un objet passe instantanément du repos à une certaine vitesse. C\'est comme si un bus venait à peine de quitter sa station et se mettait directement en vitesse de croisière, ce qui est totalement absurde. La vitesse évolue, augmente, diminue (feu rouge, montée de passagers) et augmente lentement jusqu\'à atteindre une valeur plus ou moins constante lorsqu\'il voyage sur la route. Ainsi, un bus qui voyage normalement sur une route à environ 100 km/h mettra plus de 8 heures pour parcourir 800 km car il faut tenir compte des fluctuations de vitesse. À la fin, il aura mis 10 heures pour parcourir 800 km à une vitesse moyenne de 80 km/h.

Si l\'on veut connaître la vitesse à chaque instant, il faut prendre un temps si petit que pendant celui-ci, la vitesse peut être considérée comme approximativement constante. Ainsi, la vitesse moyenne estimée de cette manière est équivalente à la vitesse existante à l\'instant considéré.

C\'est pourquoi nous parlons de la vitesse instantanée.

ID:(16, 0)

Noter

Si nous prenons un temps ($t$) avec une position ($s$) ($s(t)$) et observons un point à un moment futur $t+\Delta t$ avec une position $s(t+\Delta t)$, nous pouvons estimer la vitesse comme la distance parcourue dans le temps $\Delta t$:

$s(t+\Delta t)-s(t)$

a vitesse ($v$) peut être calculé en divisant la distance parcourue par le temps écoulé:

$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$

À mesure que la valeur de $\Delta t$ devient plus petite, la vitesse calculée se rapproche de la tangente à la courbe de position au moment:

Cela généralise ce qui avait déjà été observé pour le cas d'une vitesse constante.

ID:(1638, 0)

Citation

L'intégrale de a vitesse ($v$) correspond à l'aire sous la courbe qui définit cette fonction. Par conséquent, l'intégrale de la vitesse entre le temps initial ($t_0$) et le temps ($t$) correspond à la distance parcourue entre a vitesse ($s_0$) et a position ($s$).

Nous avons donc :



Ce qui est représenté dans le graphique suivant :

ID:(2242, 0)

Exercer

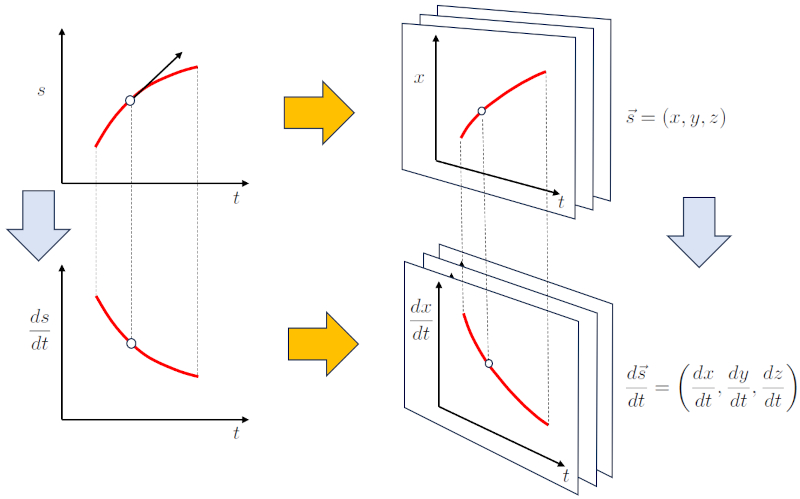
Pour les mouvements se produisant dans plus d'une dimension, la description du mouvement dans une seule dimension doit être généralisée. Cela se fait en travaillant avec une version à plusieurs dimensions de la position. Dans le cas de trois dimensions, cela se présente comme suit :

$s \rightarrow \vec{s} = (x, y, z)$

De manière analogue, la dérivée du vecteur par rapport au temps peut être définie, donnant ainsi naissance au vecteur vitesse :

$v=\displaystyle\frac{ds}{dt} \rightarrow \displaystyle\frac{d\vec{s}}{dt} = \left(\displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt}, \displaystyle\frac{dz}{dt}\right) = (v_x, v_y, v_z) = \vec{v}$

Ceci peut être résumé dans la représentation graphique suivante :

ID:(15506, 0)

Équation

Dans le cas d'une dimension, a vitesse ($v$) est liée à A position ($s$) par sa dérivée en le temps ($t$), tandis que l'intégrale de a vitesse ($v$) sur l'intervalle de le temps ($t$) à Le temps initial ($t_0$) fournit a position ($s$) à partir de a vitesse ($s_0$). Dans un contexte plus général, en plus d'une dimension, la fonction a position (vector) ($\vec{s}$) peut être dérivée en le temps ($t$), ce qui donne a vitesse (vector) ($\vec{v}$).

ID:(15391, 0)