Wenn sich ein Objekt mit konstanter Geschwindigkeit bewegt, legt es in gleichen Zeitabst nden gleiche Strecken zur ck. In diesem Fall ndert sich die Position linear mit der verstrichenen Zeit.

Um dieses Modell zu verstehen, starten Sie die Simulation mit dem Button Start und stoppen Sie sie mit Stop. Beobachten Sie dann die Werte auf dem unteren Lineal: die Zurückgelegte Strecke in einer Zeit ($\Delta s$), und auf der Stoppuhr: der Abgelaufene Zeit ($\Delta t$). Wenn Sie den ersten durch den zweiten teilen, erhalten Sie die eingegebene Geschwindigkeit: die Konstante Geschwindigkeit ($v_0$).

simulation

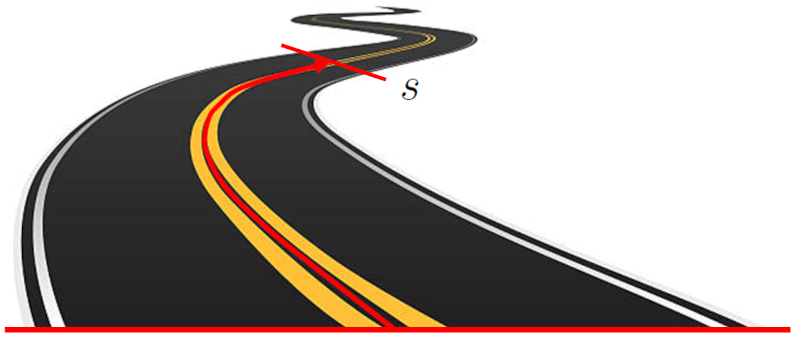
Die Position ($s$) eines Objekts in einem eindimensionalen System bezieht sich auf den Standort des Objekts in Bezug auf einen Referenzpunkt. Diese Lage wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt ausgedr ckt. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekr mmten Pfad folgen.

image

Position entlang einer Stra e entlang ihrer Achse

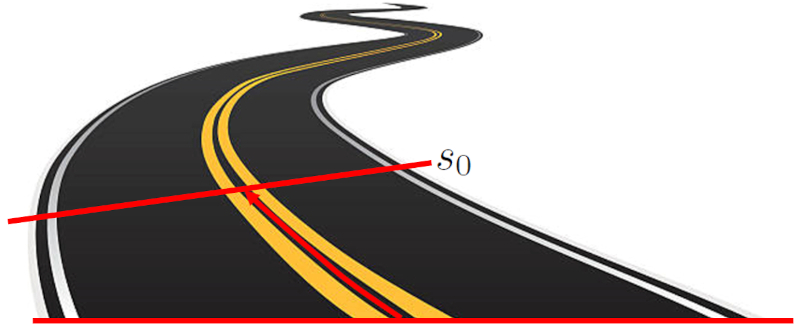
Die Ausgangsstellung ($s_0$) ist der Startort eines Objekts, bevor sich dieses bewegt. Diese Position wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt definiert. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekr mmten Pfad folgen.

image

Anfangsposition entlang einer Stra e, die ihrer Achse folgt

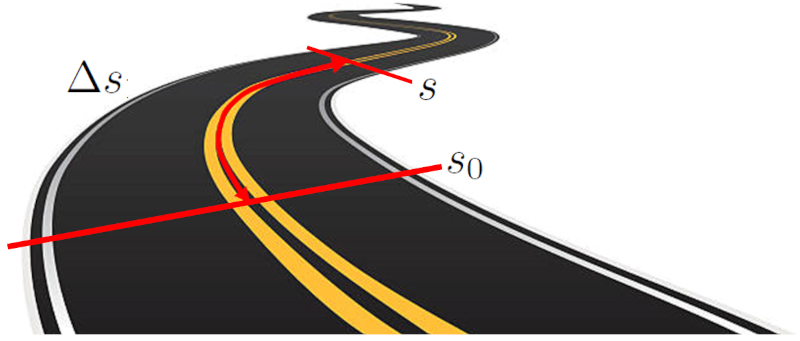
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) wird f r ein Objekt bestimmt, indem die Entfernung zwischen zwei bestimmten Punkten entlang eines Pfads gemessen wird. Dieser Pfad kann eine gerade Linie in einem kartesischen Koordinatensystem oder eine gekr mmte Bahn sein. Die Entfernung wird als die L nge des Pfads berechnet, der die Anfangs- und Endpunkte verbindet.

image

Zur ckgelegte Strecke von einem Anfangspunkt zu einem Endpunkt

Da der Wert von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) berechnet wird:

equation=4352

ist es m glich, den Ursprung der Position zu verschieben, indem ein konstanter Wert $d$ zu beiden Gr en addiert wird:

$s \rightarrow s + d$

$s_0 \rightarrow s_0 + d$

ohne das Ergebnis der zur ckgelegten Strecke zu beeinflussen:

$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$

Dieses Konzept wird als r umliche Invarianz bezeichnet, was bedeutet, dass der Wert der zur ckgelegten Strecke nicht davon abh ngt, wo genau die Messung beginnt.

Das bedeutet, dass die mit diesem Prinzip formulierten Gesetze r umlich invariant sind, das hei t, sie gelten unabh ngig davon, wo die Messung durchgef hrt wird.

Die Entwicklung jedes Systems wird durch verschiedene Parameter beschrieben, die jeweils nach einer Skala, der Zeit ($t$), entwickeln.

image

Zeit, die von einer Uhr angezeigt wird, entweder der Wert, den sie markiert, oder die Zeit

Traditionell wurde Zeit in der klassischen Physik als absolut betrachtet, gleich in allen Referenzsystemen. Die Relativit tstheorie hat diesen Begriff jedoch verallgemeinert und er muss nun als einzigartig f r jedes Referenzsystem angesehen werden, das in seiner Entwicklung unterschiedlich sein kann.

Systeme sind zeitinvariant, was bedeutet, dass ihr Verhalten nicht von dem Zeitpunkt abh ngt, wann der Prozess beginnt. Dies erm glicht es uns, der Startzeit ($t_0$), auf das Bequemste zu w hlen. Dies k nnte auf dem Instrument basieren, das verwendet wird, um die Zeit zu messen oder die Berechnungen zu erleichtern.

image

Der Zeitpunkt, zu dem die Messung beginnt, ob fest oder nach System (Chronometer)

Letztendlich kann der Beginnzeitpunkt frei gew hlt werden.

Die Grundlage f r die Beschreibung jeder Entwicklung ist die Definition der Zeit, in der sie beschrieben wird. Insbesondere wird mit der Abgelaufene Zeit ($\Delta t$) seit einem Referenzzeitpunkt gearbeitet.

image

Die Stoppuhr zeigt uns direkt die verstrichene Zeit an, seit ihre Anfangszeit Null ist

Im Falle eines Stoppuhrs wird die verstrichene Zeit seit Beginn der Messung gemessen, d.h. eine Null-Startzeit ($t_0=0$).

image

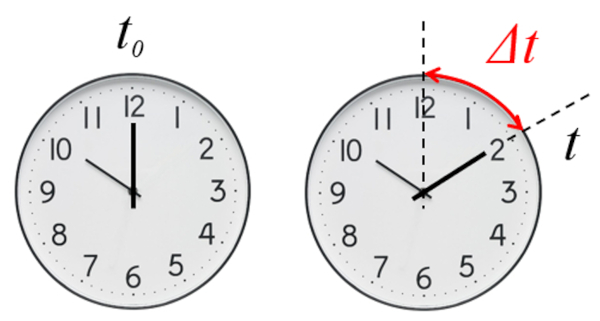
Im Fall der Uhr ist es notwendig, den Anfangstyp zu definieren, um die verstrichene Zeit zu bestimmen.

Im Falle einer Uhr wird die verstrichene Zeit seit einem definierten Startzeitpunkt gemessen, der null oder ungleich null sein kann.

Da der Abgelaufene Zeit ($\Delta t$) als die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) berechnet wird:

equation=4353

ist es m glich, den Zeitursprung zu "verschieben", indem ein konstanter Wert

zu beiden Gr en hinzugef gt wird:

$t \rightarrow t + \tau$

$t_0 \rightarrow t_0 + \tau$

ohne das Ergebnis der verstrichenen Zeit zu beeinflussen:

$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$

Dieses Konzept wird als zeitliche Invarianz bezeichnet, was bedeutet, dass der Wert der verstrichenen Zeit unabh ngig vom spezifischen Startpunkt der Messung unver ndert bleibt.

Dies bedeutet, dass die mit diesem Prinzip formulierten Gesetze zeitlich invariant sind, d. h., sie gelten unabh ngig davon, ob sie in der Gegenwart, der Vergangenheit oder der Zukunft angewendet werden.

Um zu sch tzen, wie sich ein Objekt bewegt, m ssen wir den Weg-Zeit-Verlauf kennen. Daher wird das Verh ltnis zwischen dem zur ckgelegten Weg und der vergangenen Zeit als Durchschnittsgeschwindigkeit definiert.

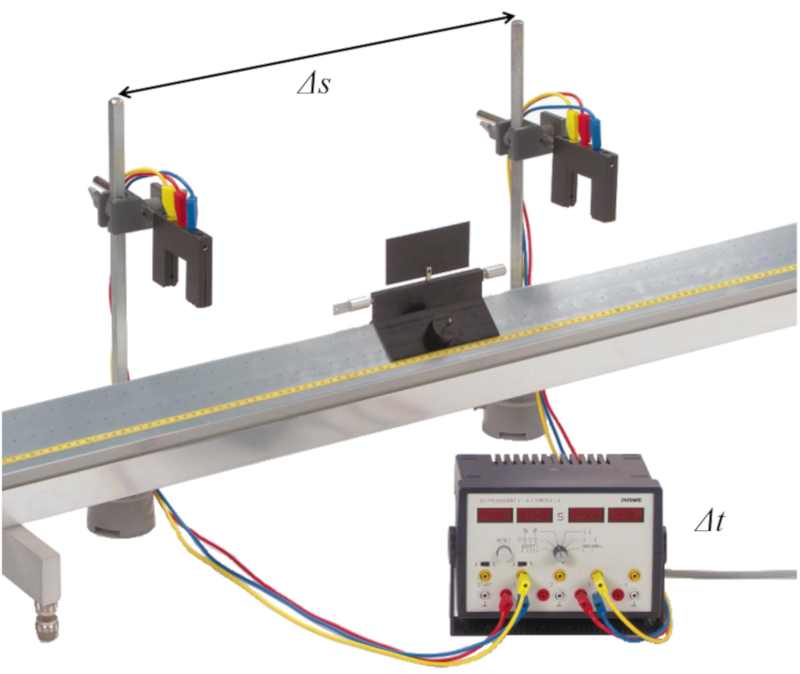
Um die Messung durchzuf hren, kann ein System wie das in der Abbildung verwendet werden:

image

Um die Durchschnittsgeschwindigkeit zu bestimmen, m ssen zwei Sensoren platziert werden, die den Durchgang eines Objekts in einem Abstand $\Delta s$ registrieren. Dann wird der Zeitunterschied registriert, wenn das Objekt jeden Sensor passiert $\Delta t$. Mit beiden Werten wird die Durchschnittsgeschwindigkeit bestimmt, indem die zur ckgelegte Entfernung durch die vergangene Zeit dividiert wird.

Die Gleichung, die die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) beschreibt, lautet wie folgt:

equation=3152

Es ist zu beachten, dass die Durchschnittsgeschwindigkeit eine Sch tzung der tats chlichen Geschwindigkeit ist. Das Hauptproblem liegt darin, dass:

Wenn sich die Geschwindigkeit w hrend der vergangenen Zeit ndert, kann der Wert der Durchschnittsgeschwindigkeit sehr unterschiedlich von einer Durchschnittsgeschwindigkeit sein.

Zus tzlich gibt es ein Problem bei der Messung der zur ckgelegten Entfernung, da mit zwei Positionen gearbeitet wird. Dies kann dazu f hren, dass

Da der zur ckgelegte Weg aus der Differenz zweier Positionen berechnet wird, kann es passieren, dass sich die Anfangs- und Endposition im Falle einer Bewegungsumkehr w hrend der vergangenen Zeit sehr hnlich sind. Dies kann zu einer Durchschnittsgeschwindigkeit f hren, die ann hernd null ist, obwohl ein \\\\\"langer\\\\\" Weg zur ckgelegt wurde.

Deshalb ist der Schl ssel,

Die Geschwindigkeit in einer ausreichend kurzen vergangenen Zeit zu bestimmen, damit ihre nderung minimal ist.

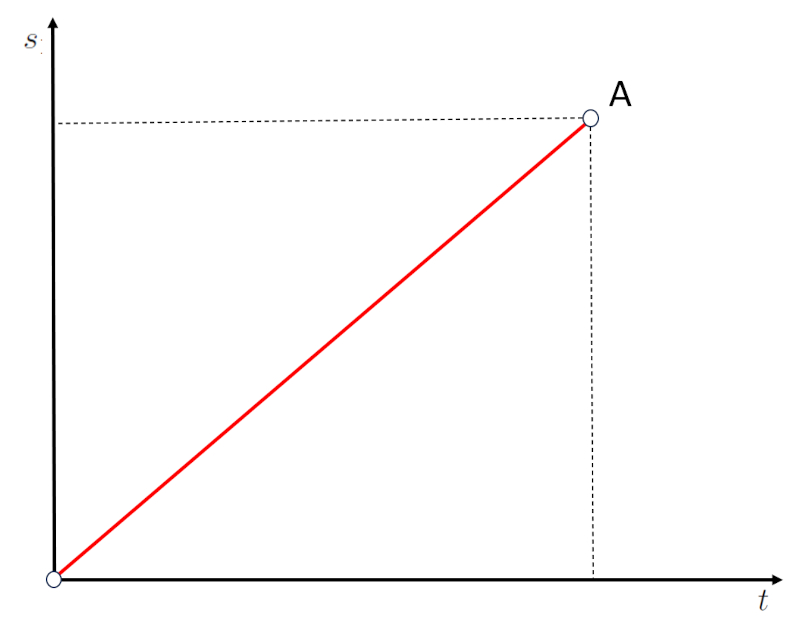
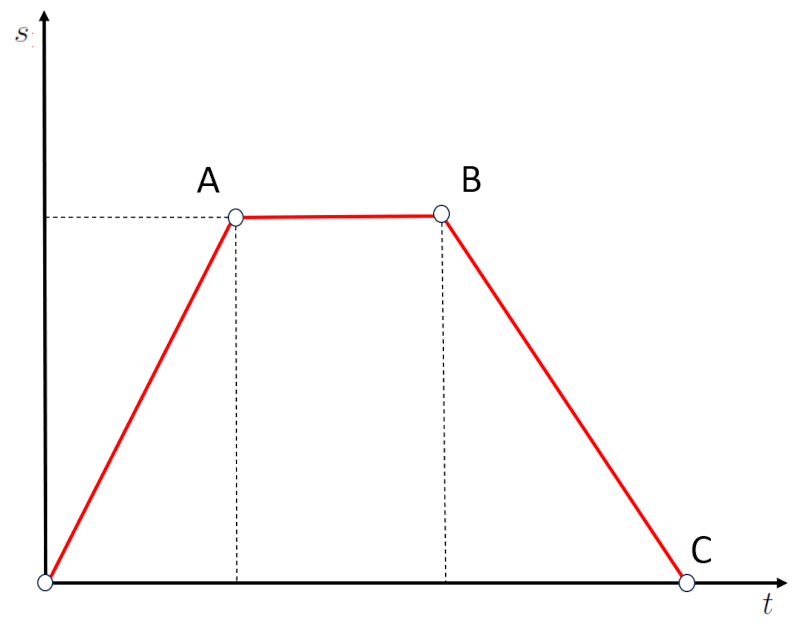
Wenn die Verschiebung als eine Linie zwischen dem Ursprung O und dem Punkt A dargestellt wird:

image

Sieht man, dass eine Strecke in einer bestimmten Zeit zur ckgelegt wurde. Daher entspricht die Steigung der Grafik Strecke vs. Zeit der Geschwindigkeit.

Wenn die Steigung gr er ist, bedeutet dies, dass eine Strecke in k rzerer Zeit zur ckgelegt wird, was einer h heren Geschwindigkeit entspricht.

Wenn die Steigung kleiner ist, bedeutet dies, dass eine Strecke in l ngerer Zeit zur ckgelegt wird, was einer niedrigeren Geschwindigkeit entspricht.

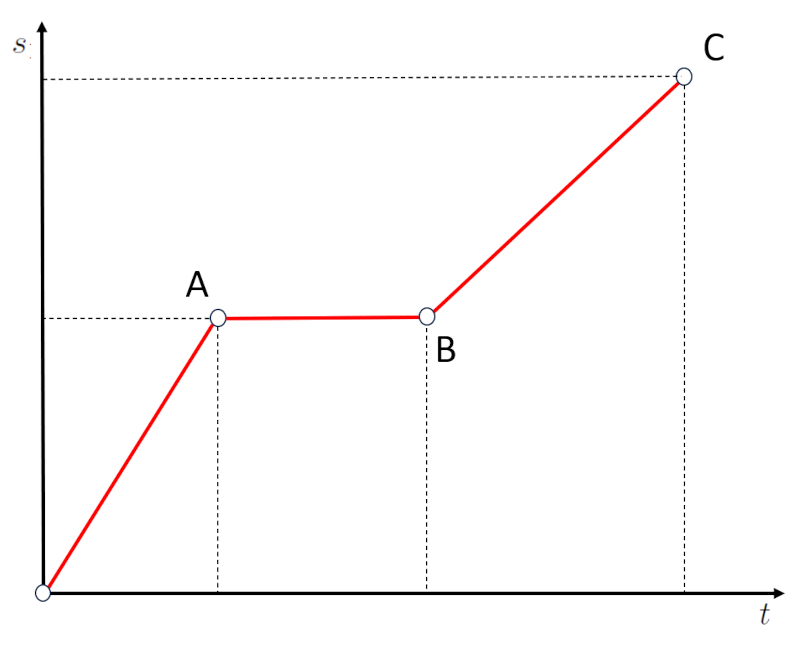
Ein zweiter Fall sind horizontale Abschnitte im Weg-Zeit-Diagramm:

image

Wenn wir uns den Abschnitt AB ansehen, werden wir feststellen, dass sich der Weg trotz verstrichener Zeit nicht ver ndert hat. Das bedeutet, dass das Objekt angehalten ist. Daher entsprechen horizontale Abschnitte, die einer Nullsteigung entsprechen, Phasen, in denen die Geschwindigkeit null ist.

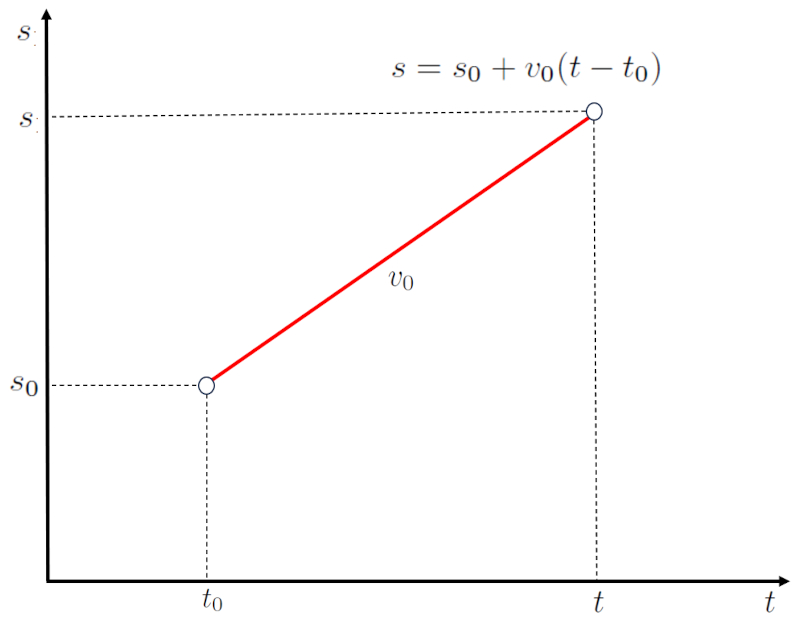
F r den Fall einer konstanten Geschwindigkeit und eines Anfangszeitpunkts kann die Position mit den Werten die Position ($s$), die Ausgangsstellung ($s_0$), die Konstante Geschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mithilfe der folgenden Gleichung berechnet werden:

equation=3154

Die Gleichung entspricht einer geraden Linie mit:

• einer Steigung von die Konstante Geschwindigkeit ($v_0$)
• einem y-Achsenabschnitt bei die Ausgangsstellung ($s_0$) f r der Startzeit ($t_0$)

wie unten dargestellt:

image

Im Fall eines Graphen mit einem Abschnitt negativer Steigung:

image

Liegt eine Situation vor, in der man von der Position B zur Position C zur ckgekehrt ist, die sich in einer Entfernung von Null befindet. Mit anderen Worten, negative Steigungen bedeuten, dass man sich in die entgegengesetzte Richtung bewegt, nicht weg vom Ursprung, sondern auf ihn zu.

Wenn sich ein K rper im "Ruhezustand" befindet, bedeutet dies, dass er im Ruhezustand bez glich unseres Bezugssystems oder Koordinatensystems ist. Dieser "Ruhezustand" ist jedoch v llig relativ, das hei t, von einem K rper aus, der sich relativ zu unserem System bewegt, ist der "ruhende" K rper auch in Bewegung.

In diesem Sinne gibt es keinen "absoluten Ruhezustand", sondern nur einen relativ zum jeweiligen Bezugssystem. Deshalb ist im Allgemeinen jede Geschwindigkeitsmessung eine Messung im Verh ltnis zu einem bestimmten Bezugssystem.

Wenn sich ein K rper zum Beispiel sehr langsam zu bewegen scheint, bedeutet dies nur, dass seine Geschwindigkeit der Geschwindigkeit des Bezugssystems, in dem die langsame Bewegung beobachtet wird, sehr hnlich ist.

Das Basismodell bezieht sich auf die Position ($s$), gemessen von einem Ursprung die Ausgangsstellung ($s_0$), was zu eine Zurückgelegte Strecke in einer Zeit ($\Delta s$) f hrt, und der Zeit ($t$), gemessen von einem Ursprung der Startzeit ($t_0$), was zu der Abgelaufene Zeit ($\Delta t$) f hrt. Aus diesen Differenzen ergibt sich die Mittlere Geschwindigkeit ($\bar{v}$), das, wenn es als konstant angenommen wird, die Konstante Geschwindigkeit ($v_0$) entspricht.

Die Basisbeziehung des Modells ist die Gerade, die die zentralen Variablen des Modells verbindet:

image=2243

Damit ist die Netzwerkstruktur des Modells:

model

Wir k nnen die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:

kyon

Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:

kyon

Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:

kyon

Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zur ckgelegte Weg in Abh ngigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:

kyon

Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.