Momentane Beschleunigung
Storyboard 
Um zu beschreiben, wie sich die Geschwindigkeit im Laufe der Zeit entwickelt, muss der zeitliche Verlauf untersucht werden.
Das Verhältnis der Variation der Geschwindigkeit entspricht der Variation der Geschwindigkeit in der verstrichenen Zeit, die dividiert durch diese der Beschleunigung entspricht.
Für eine infinitesimal verstrichene Zeit entspricht die Beschleunigung der momentanen Beschleunigung.
ID:(1433, 0)
Momentane Beschleunigung
Storyboard 
Um zu beschreiben, wie sich die Geschwindigkeit im Laufe der Zeit entwickelt, muss der zeitliche Verlauf untersucht werden. Das Verhältnis der Variation der Geschwindigkeit entspricht der Variation der Geschwindigkeit in der verstrichenen Zeit, die dividiert durch diese der Beschleunigung entspricht. Für eine infinitesimal verstrichene Zeit entspricht die Beschleunigung der momentanen Beschleunigung.
Variablen
Berechnungen
Berechnungen
Gleichungen
Da ein Vektor als eine Anordnung seiner verschiedenen Komponenten ausgedr ckt werden kann,
$\vec{v}=(v_x,v_y,v_z)$
kann seine Ableitung als Ableitung jeder seiner Komponenten ausgedr ckt werden:
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
Im Allgemeinen gilt, dass die instantane Geschwindigkeit in mehr als einer Dimension
Wenn wir die Differenz von die Geschwindigkeit ($v$) zu den Zeiten $t+\Delta t$ und $t$ betrachten:
$\Delta v = v(t+\Delta t)-v(t)$
und $\Delta t$ als der Abgelaufene Zeit ($\Delta t$) nehmen, dann im Grenzwert von infinitesimal kurzen Zeiten:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Diese letzte Ausdruck entspricht der Ableitung der Funktion die Geschwindigkeit ($v$):
welche wiederum die Steigung der grafischen Darstellung dieser Funktion bei der Zeit ($t$) ist.
Wenn wir die Definition von die Augenblickliche Beschleunigung ($a$) bei der Zeit ($t$) integrieren,
bedeutet dies, dass f r ein Zeitintervall $dt$ die zur ckgelegte Strecke ist
$dv = a dt$
Wenn wir $N$ Intervalle $dt_i$ mit Beschleunigungen $a_i$ betrachten, wird die Gesamt nderung der Geschwindigkeit sein
$v - v_0 = \displaystyle\sum_i a_i dt_i$
Wenn wir die Beschleunigungs-Zeit-Kurve betrachten, entsprechen die Elemente $a_i dt_i$ Rechtecken mit der H he $a_i$ und der Breite $dt_i$. Die Summe entspricht daher der Fl che unter der Beschleunigungs-Zeit-Kurve. Daher kann die Summe als Integral ausgedr ckt werden:
Da die Augenblickliche Beschleunigung ($a$) die Ableitung von die Geschwindigkeit ($v$) nach der Zeit ($t$) ist,
und die Geschwindigkeit ($v$) die Ableitung von die Position ($s$) nach der Zeit ($t$) ist,
haben wir
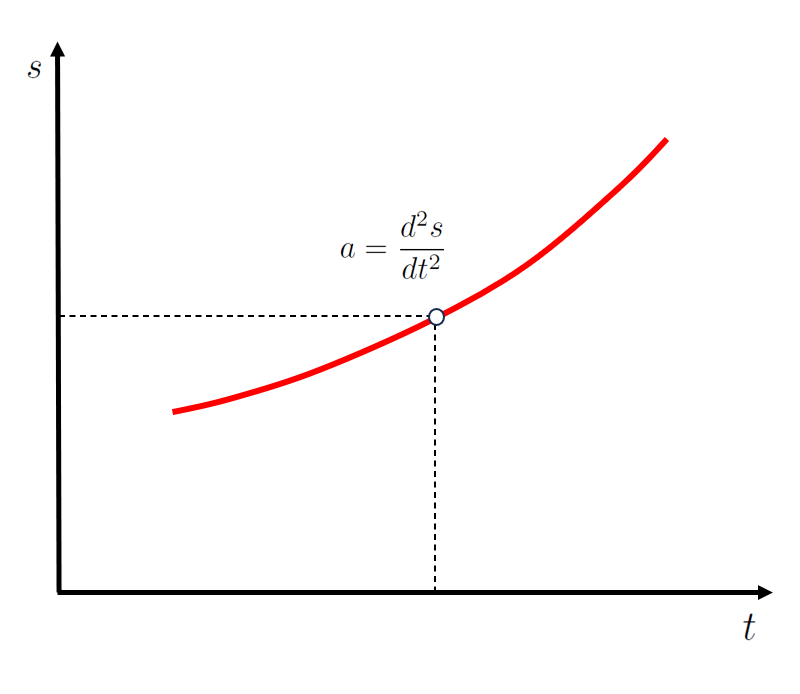
$a=\displaystyle\frac{dv}{dt}=\displaystyle\frac{d}{dt}\displaystyle\frac{ds}{dt}=\displaystyle\frac{d^2s}{dt^2}$
daher
Beispiele
Auf der einen Seite ist es wichtig, zwischen dem einfachsten, eindimensionalen Fall und dem mehrdimensionalen Fall zu unterscheiden. F r beide F lle ist die Ableitung von die Geschwindigkeit ($v$) nach der Zeit ($t$), was der Anstieg der Kurve von die Geschwindigkeit ($v$) entspricht, gleich die Augenblickliche Beschleunigung ($a$). Ebenso ist die Ableitung von die Geschwindigkeit (Vektor) ($\vec{v}$) nach der Zeit ($t$), was die Geschwindigkeit (Vektor) ($\vec{v}$) entspricht.
Beschleunigung wird definiert als nderung der Geschwindigkeit pro Zeiteinheit. Diese Definition bezieht sich jedoch auf die durchschnittliche Beschleunigung, die w hrend eines bestimmten Zeitintervalls existiert.
Diese Einschr nkung der durchschnittlichen Beschleunigung spiegelt sich in Situationen wider, in denen ein Objekt beschleunigt und dann abgebremst wird, bis es zum Stillstand kommt. In diesem Fall betr gt die durchschnittliche Beschleunigung null, was suggeriert, dass das Objekt berhaupt nicht beschleunigt hat. Dies ist jedoch nicht wahr, da das Objekt sowohl w hrend der Beschleunigungsphase als auch w hrend der Abbremsphase bewegt wird.
Um die Beschleunigung zu jedem Zeitpunkt zu bestimmen, muss ein kleines Zeitintervall betrachtet werden, so dass die Beschleunigung w hrend dieser Zeit als ann hernd konstant angenommen werden kann. Die so gesch tzte durchschnittliche Beschleunigung entspricht der Beschleunigung, die zum betrachteten Zeitpunkt vorliegt.
Daher wird der Begriff 'momentane Beschleunigung' verwendet, um sich auf die Beschleunigung zu einem bestimmten Zeitpunkt zu beziehen.
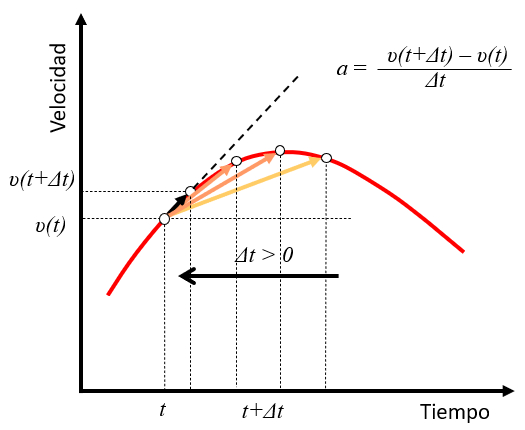
Wenn wir der Abgelaufene Zeit ($\Delta t$) nehmen und ein Objekt in Bewegung mit der Geschwindigkeit die Geschwindigkeit ($v$) beobachten, und dann das gleiche Objekt zu einem sp teren Zeitpunkt $t+\Delta t$ mit der Geschwindigkeit $v(t+\Delta t)$ beobachten, k nnen wir seine Beschleunigung als die nderung der Geschwindigkeit w hrend der Abgelaufene Zeit ($\Delta t$) sch tzen:
$a\sim\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}$
Wenn der Wert von $\Delta t$ kleiner wird, n hert sich dieser Ausdruck f r die Beschleunigung der momentanen nderungsrate der Geschwindigkeit zum Zeitpunkt $t$, oder anders gesagt, der Steigung der Tangente an der Geschwindigkeitskurve an diesem Punkt an:
Dies verallgemeinert das Konzept von die Augenblickliche Beschleunigung ($a$) f r den Fall von die konstante Beschleunigung ($a_0$), wie bereits zuvor gesehen, ausgedr ckt als die Ableitung von die Geschwindigkeit ($v$) bez glich der Zeit ($t$):
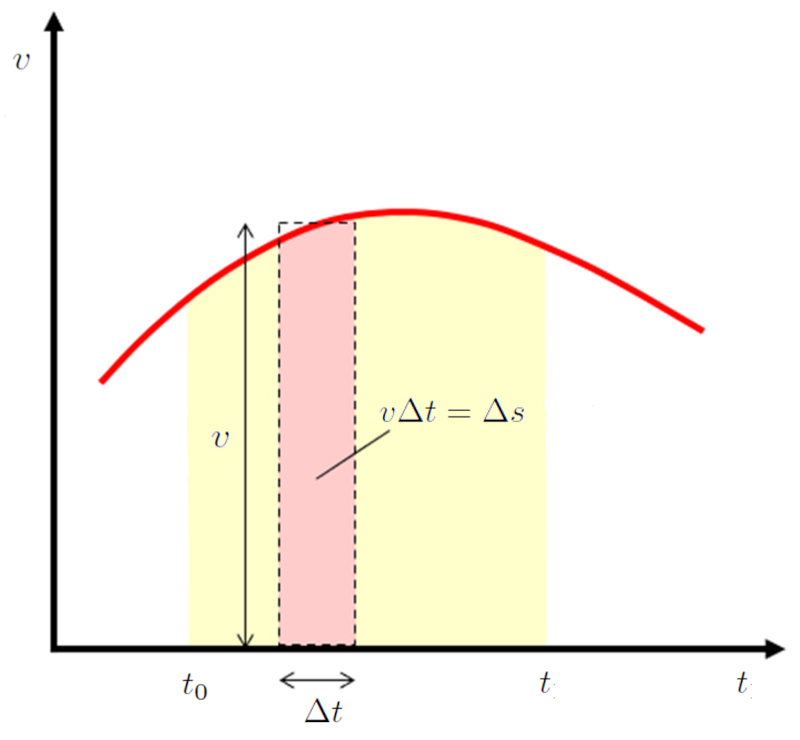
Wenn man beobachtet, dass die Geschwindigkeit ($v$) gleich die Zurückgelegte Strecke in einer Zeit ($\Delta s$) pro der Abgelaufene Zeit ($\Delta t$) ist, deutet dies darauf hin, dass der Weg gegeben ist durch:
$\Delta s = v\Delta t$
Da das Produkt $v\Delta t$ die Fl che unter der Geschwindigkeits-zu-Zeit-Kurve repr sentiert, was auch gleich dem zur ckgelegten Weg ist:
Diese Fl che kann auch mit dem Integral der entsprechenden Funktion berechnet werden. Daher entspricht das Integral der Beschleunigung zwischen der Startzeit ($t_0$) und der Zeit ($t$) der nderung der Geschwindigkeit zwischen der Anfangsgeschwindigkeit die Anfangsgeschwindigkeit ($v_0$) und die Geschwindigkeit ($v$):
Die Augenblickliche Beschleunigung ($a$) ist gleich der Ableitung von die Geschwindigkeit ($v$) nach der Zeit ($t$):
Und da die Geschwindigkeit ($v$) die Ableitung von die Position ($s$) nach der Zeit ($t$) ist:
Daher ist die Augenblickliche Beschleunigung ($a$) die zweite Ableitung von die Position ($s$) nach der Zeit ($t$),
was der Kr mmung der Kurve die Position ($s$) als Funktion von der Zeit ($t$) entspricht:
Im Fall einer Dimension ist die Augenblickliche Beschleunigung ($a$) durch seine Ableitung bei der Zeit ($t$) mit die Geschwindigkeit ($v$) verbunden, w hrend das Integral von die Augenblickliche Beschleunigung ($a$) ber das Intervall von der Zeit ($t$) bis der Startzeit ($t_0$) Die Geschwindigkeit ($v$) ab die Anfangsgeschwindigkeit ($v_0$) liefert. In einem allgemeineren Kontext, in mehr als einer Dimension, kann die Funktion die Geschwindigkeit (Vektor) ($\vec{v}$) bei der Zeit ($t$) abgeleitet werden, was zu die Geschwindigkeit (Vektor) ($\vec{v}$) f hrt.
Die Variable die Mittlere Beschleunigung ($\bar{a}$), berechnet als nderung in die Geschwindigkeit Unterschied ($\Delta v$) geteilt durch das Intervall von der Abgelaufene Zeit ($\Delta t$) mittels
ist eine N herung der tats chlichen Beschleunigung, die dazu neigt, sich zu verzerren, wenn die Beschleunigung w hrend des Zeitintervalls schwankt. Daher wird das Konzept von die Augenblickliche Beschleunigung ($a$) eingef hrt, das ber ein sehr kleines Zeitintervall bestimmt wird. In diesem Fall beziehen wir uns auf ein unendlich kleines Zeitintervall, und die Geschwindigkeits nderung ber die Zeit reduziert sich auf die Ableitung von die Geschwindigkeit ($v$) nach der Zeit ($t$):
was der Ableitung der Geschwindigkeit entspricht.
Wenn die Augenblickliche Beschleunigung ($a$) der Ableitung von die Geschwindigkeit ($v$) bei der Zeit ($t$) entspricht,
dann ist die Geschwindigkeit ($v$) gleich die Anfangsgeschwindigkeit ($v_0$), und die Integration der Beschleunigung von der Startzeit ($t_0$) bis der Zeit ($t$) ist:
Da die Augenblickliche Beschleunigung ($a$) die Steigung von die Geschwindigkeit ($v$) in Bezug auf der Zeit ($t$) darstellt,
und die Geschwindigkeit ($v$) wiederum die Steigung von die Position ($s$) in Bezug auf der Zeit ($t$) ist,
k nnen wir die Augenblickliche Beschleunigung ($a$) als die zweite Ableitung von die Position ($s$) nach der Zeit ($t$) ausdr cken.
Im Allgemeinen sollte die Geschwindigkeit als ein dreidimensionaler Vektor verstanden werden. Das hei t, ihre die Position ($s$) muss durch einen Vektor eine Posición (Vektor) ($\vec{s}$) beschrieben werden, f r den jede Komponente die Geschwindigkeit ($v$) definiert werden kann, wie in der folgenden Gleichung gezeigt:
Dies erm glicht eine Verallgemeinerung von die Geschwindigkeit (Vektor) ($\vec{v}$) wie folgt:
ID:(1433, 0)