Constant speed
Storyboard 
To describe how the position changes over time, one must study its variation through time.
The relationship between the change in position is equivalent to the distance traveled over the elapsed time, which, when divided by that time, becomes the speed.
For a finite elapsed time, the speed corresponds to the average speed during that interval.
Note: Velocity encompasses speed while also incorporating directional information.
ID:(608, 0)
Mechanisms
Definition 
The key to describing motion at a constant velocity is understanding the concept of:
• Position,
• Displacement,
• Time, and
• Elapsed time
to define velocity. Finally, graphical representation and interpretation are discussed.
ID:(15379, 0)
Position
Image 
The position ($s$) of an object in a one-dimensional system refers to the location of the object in relation to a reference point. This location is expressed as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis, or it can follow a curved path:
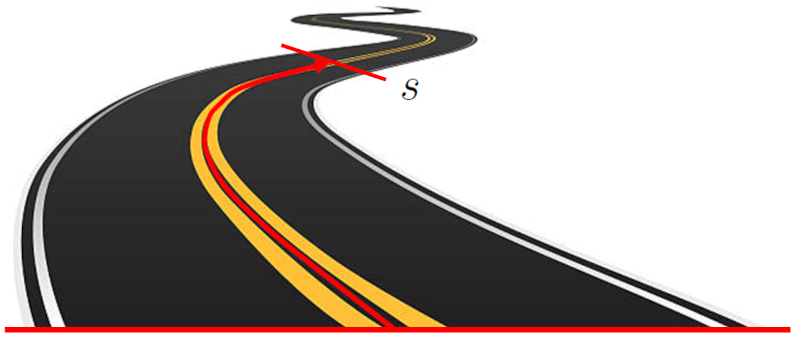
ID:(15, 0)
Initial position
Note 
The starting position ($s_0$) is the starting location of an object before any motion begins. This location is defined as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis or it can follow a curved path.
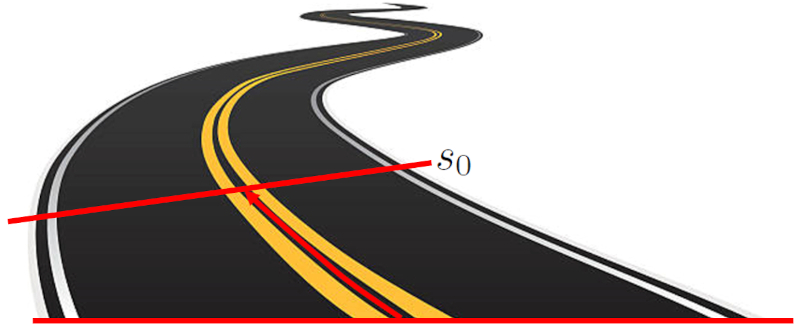
ID:(10302, 0)
Distance traveled
Quote 
The distance traveled in a time ($\Delta s$) by an object is measured by measuring the distance between two specific points along a trajectory. This trajectory can be a straight line on a Cartesian axis or a curved path. The distance is calculated by measuring the length of the trajectory between the two starting and ending points.
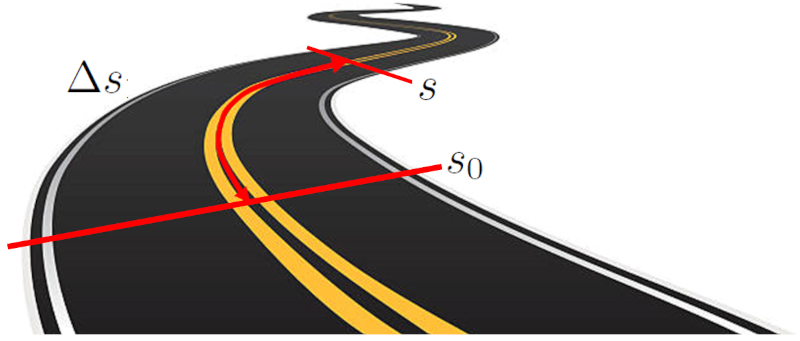
ID:(9495, 0)
Time
Exercise 
The evolution of any system is described by different parameters, each one evolving according to a scale called the time ($t$).

Traditionally, time was considered absolute in classical physics, being the same in all reference systems. However, the theory of relativity has generalized this concept and now it must be seen as unique to each reference system, being able to differ in its advancement.
ID:(478, 0)
Initial time
Equation 
Systems are time-invariant, meaning that their behavior is not affected by when the process begins. This allows us to choose the start Time ($t_0$), based on what is most convenient. This could be based on the instrument used to measure the time or to make calculations easier.
Ultimately, the beginning time can be chosen freely.
ID:(715, 0)
Time elapsed
Script 
The foundation of describing any evolution is the definition of time in which it is described. Specifically, we work with the time elapsed ($\Delta t$) from a reference time.

• In the case of a stopwatch, the elapsed time is measured from the start of its measurement, i.e., a zero initial time ($t_0=0$).
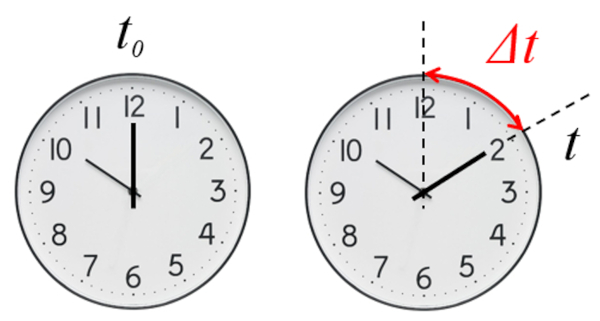
• In the case of a clock, the elapsed time is measured from a defined initial time, which may or may not be zero.
ID:(12507, 0)
Average speed
Variable 
To estimate how an object moves, we need to know the path over time it follows. Hence, the ratio of the distance traveled and the time elapsed, which is defined as the average velocity, is introduced.
To measure this, we can use a system like the one shown in the image:
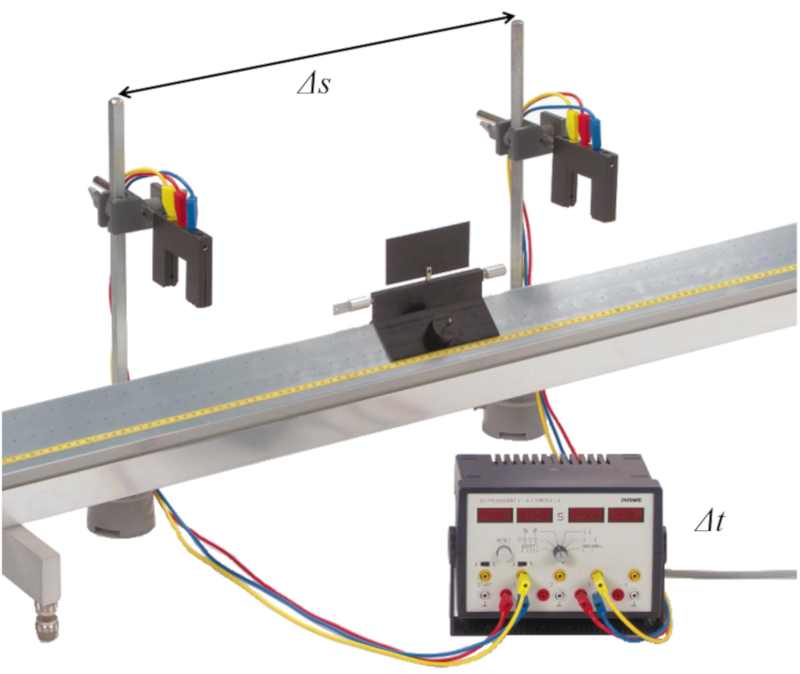
To determine the average velocity, two sensors must be placed to record the passage of an object at a distance $\Delta s$. The time difference in which the object passes in front of each sensor is then recorded as $\Delta t$. The average velocity is determined by dividing the distance traveled by the time elapsed.
The equation that describes the mean Speed ($\bar{v}$) with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) is the following:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
It should be noted that the average velocity is an estimate of the actual velocity. The main problem lies in the fact that:
If the velocity changes during the elapsed time, the value of the average velocity can be very different from the average speed.
Additionally, there is a problem with the way the distance traveled is measured, as we work with two positions. This can lead to the situation where:
Since the path traveled is calculated from the difference between two positions, in cases where the movement is reversed during the elapsed time, the initial and final positions can be very similar. This can lead to an average velocity that is approximately zero, despite having traveled a 'long' distance.
Therefore, the key is to:
Determine the velocity in a sufficiently short elapsed time so that its variation is minimal.
ID:(470, 0)
Velocity as slope of position curve
Audio 
If displacement is graphed as a line between the origin O and point A:
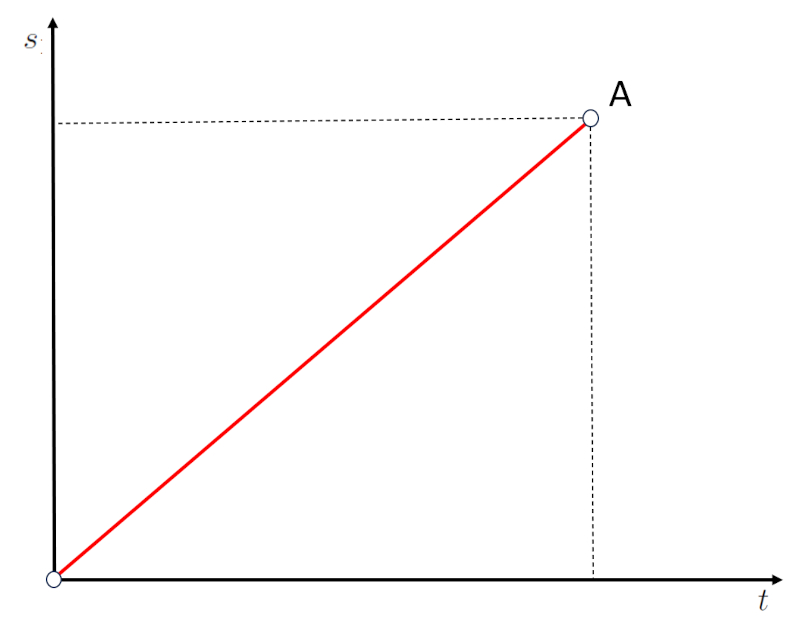
it can be seen that a path has been traveled over a period of time. Therefore, the slope of the graph of path vs elapsed time corresponds to velocity.
If the slope is steeper, it means that a path is covered in less time, which corresponds to a higher velocity.
If the slope is flatter, it means that a path is covered in more time, which corresponds to a lower velocity.
ID:(2239, 0)
Time path diagram with horizontal segment
Video 
A second type of case is horizontal segments in the distance vs time graph:
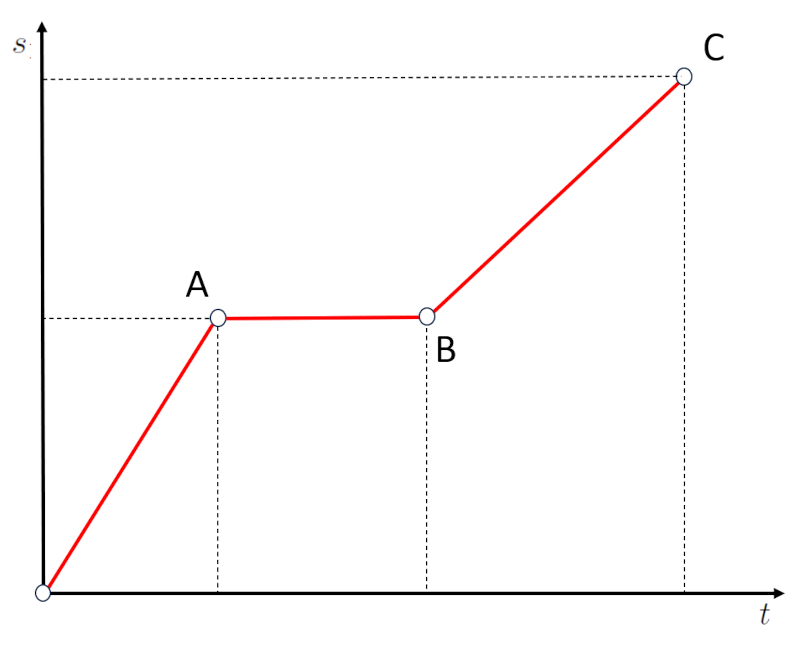
If we observe segment AB, we will notice that despite the elapsed time, the distance has not changed. This means that the object is at rest. Therefore, horizontal segments, which correspond to zero slope, correspond to periods when the velocity is zero.
ID:(2241, 0)
Time path graph for constant speed and initial time
Unit 
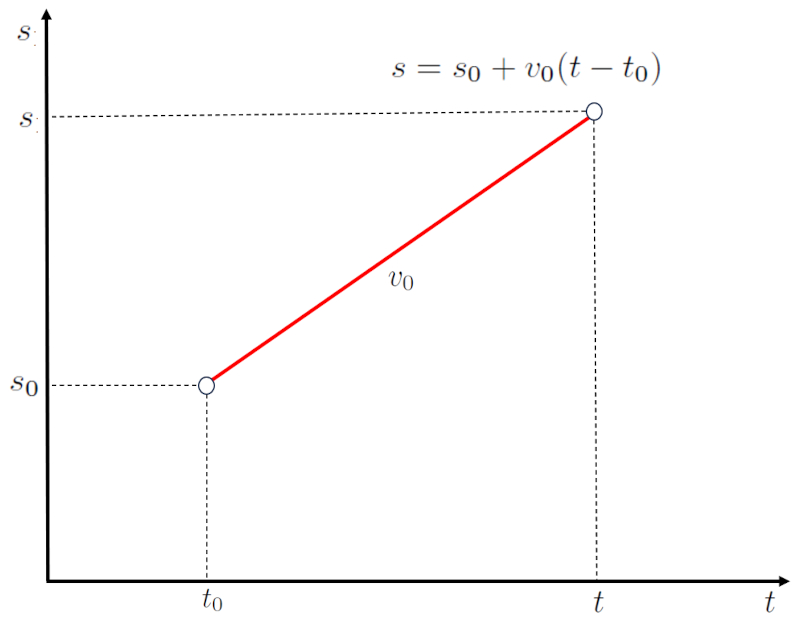
For the case of constant velocity and initial time, the position can be calculated using the values the position ($s$), the starting position ($s_0$), the constant velocity ($v_0$), the time ($t$), and the start Time ($t_0$) with the following equation:
| $ s = s_0 + v_0 ( t - t_0 )$ |
which corresponds to a straight line with:
• a slope equal to the constant velocity ($v_0$)
• a y-intercept at the starting position ($s_0$) for the start Time ($t_0$)
as illustrated below:
ID:(2243, 0)
Negative slope
Code 
When a segment on a graph has a negative slope, as shown below:
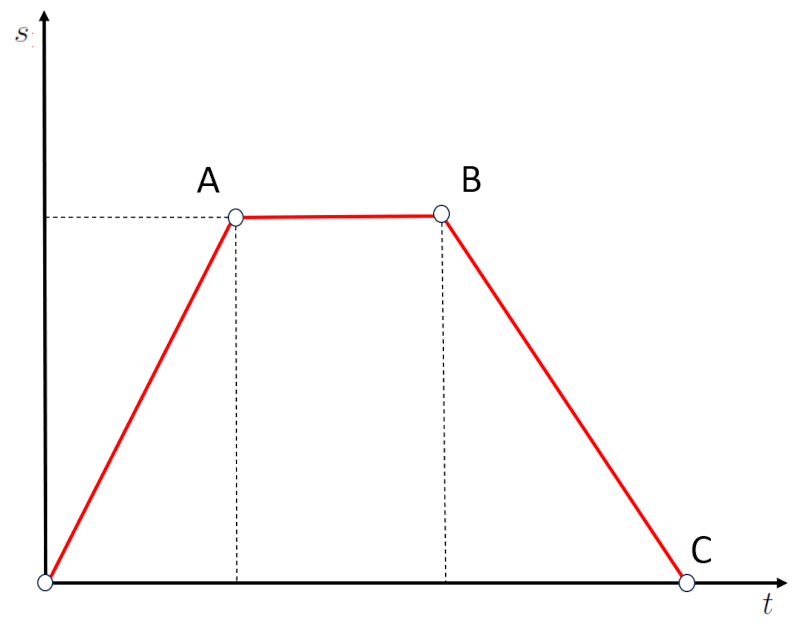
it represents a situation in which the object returned from position B to C, which is a distance of zero from the origin. In other words, negative slopes correspond to traveling in the opposite direction, not moving away but getting closer to the origin.
ID:(2245, 0)
Paradox of the body at rest
Flux 
When a body is said to be "at rest", it means that it is at rest relative to our reference frame or coordinate system. However, this "rest" is entirely relative, meaning that from a body that moves relative to our system, the body at "rest" is also in motion.
In this sense, there is no such thing as an "absolute rest", it only exists as something relative to a particular reference frame. Therefore, in general, all velocity measurements are relative to a particular reference frame.
For example, if a body appears to move very slowly, it only means that its velocity is very similar to the velocity of the reference frame in which the slow movement is observed.
ID:(4405, 0)
Model
Matrix 
The base model relates the position ($s$), measured from an origin the starting position ($s_0$), resulting in ERROR:6025.1, and the time ($t$), measured from an origin the start Time ($t_0$), resulting in the time elapsed ($\Delta t$). From these differences, the mean Speed ($\bar{v}$) is defined, which, if assumed constant, is equal to the constant velocity ($v_0$).
The base relationship of the model is the straight line that associates the central variables of the model:

With this, the network structure of the model is:
ID:(15378, 0)
Constant velocity
Description 
To describe how position evolves over time, it is necessary to analyze its variation throughout time.
The relationship between the variation in position is equivalent to the distance traveled over the elapsed time, which, when divided by that time, becomes the velocity.
Variables
Calculations
Calculations
Equations
With the distance traveled in a time ($\Delta s$) it is with the position ($s$) and the starting position ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
and the time elapsed ($\Delta t$) is with the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
The equation for average velocity:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
can be written as:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
thus, solving for it we get:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Examples
When an object moves at constant speed, it covers equal distances in equal time intervals. In this case, the position changes linearly with the elapsed time.
To understand this model, run the simulation with the Start button and stop it with Stop. Then observe the values shown on the bottom ruler: the distance traveled in a time ($\Delta s$), and on the stopwatch: the time elapsed ($\Delta t$). Dividing the first by the second gives the entered velocity: the constant velocity ($v_0$).
(ID 15379)
The position ($s$) of an object in a one-dimensional system refers to the location of the object in relation to a reference point. This location is expressed as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis, or it can follow a curved path:

Position along a road following its axis
(ID 15)
The starting position ($s_0$) is the starting location of an object before any motion begins. This location is defined as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis or it can follow a curved path.

Initial position along a road following its axis
(ID 10302)
The distance traveled in a time ($\Delta s$) for an object is determined by measuring the distance between two specific points along a path. This path can be a straight line on a Cartesian axis or a curved trajectory. The distance is calculated as the length of the path connecting the initial and final points.

Distance traveled from an initial point to a final point
Since the value of the distance traveled in a time ($\Delta s$) is calculated as the difference between the position ($s$) and the starting position ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
it is possible to "shift" the origin of the position by adding a constant value $d$ to both quantities:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
without affecting the result of the distance traveled:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
This concept is known as spatial invariance, which implies that the value of the distance traveled does not depend on the specific point where the measurement begins.
This means that the laws formulated using this principle will be spatially invariant, i.e., they will remain valid regardless of the location where the measurement is made.
(ID 9495)
The evolution of any system is described by different parameters, each one evolving according to a scale called the time ($t$).
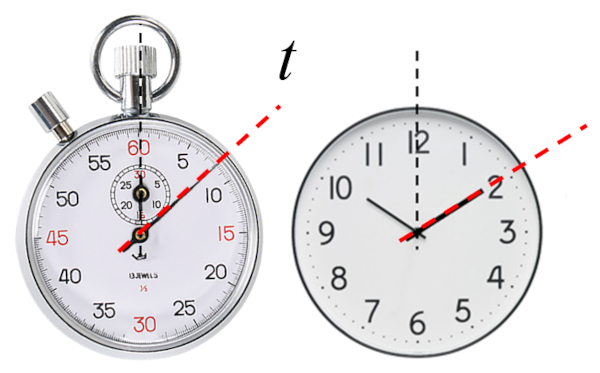
Time indicated by a clock, either the value at which it is marked or the hour
Traditionally, time was considered absolute in classical physics, being the same in all reference systems. However, the theory of relativity has generalized this concept and now it must be seen as unique to each reference system, being able to differ in its advancement.
(ID 478)
Systems are time-invariant, meaning that their behavior is not affected by when the process begins. This allows us to choose the start Time ($t_0$), based on what is most convenient. This could be based on the instrument used to measure the time or to make calculations easier.
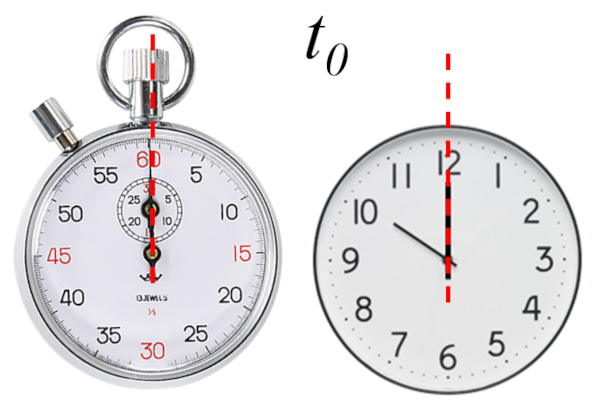
The time at which the measurement starts, whether fixed or by system (stopwatch)
Ultimately, the beginning time can be chosen freely.
(ID 715)
The foundation of describing any evolution is the definition of time in which it is described. Specifically, we work with the time elapsed ($\Delta t$) from a reference time.
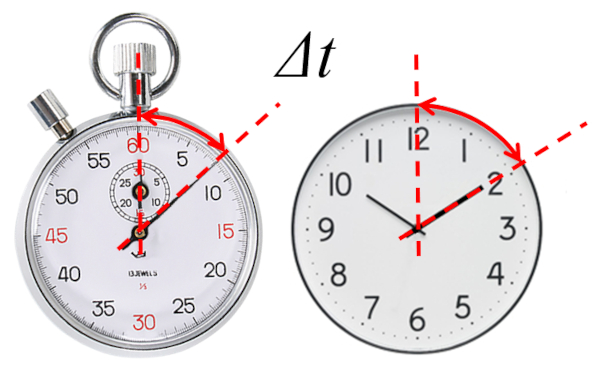
The stopwatch directly gives us the elapsed time since its initial time is zero
In the case of a stopwatch, the elapsed time is measured from the start of its measurement, i.e., a zero initial time ($t_0=0$).

In the case of the clock, it is necessary to define the initial type in order to determine the elapsed time.
In the case of a clock, the elapsed time is measured from a defined initial time, which may or may not be zero.
Since the time elapsed ($\Delta t$) is calculated as the difference between the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
it is possible to "shift" the time origin by adding a constant value
to both time points:
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
without affecting the elapsed time:
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
This property is known as temporal invariance, meaning that the elapsed time remains unchanged regardless of the specific starting point of the measurement.
Consequently, laws formulated using this principle will be temporally invariant, meaning they remain valid whether applied in the present, the past, or the future.
(ID 12507)
To estimate how an object moves, we need to know the path over time it follows. Hence, the ratio of the distance traveled and the time elapsed, which is defined as the average velocity, is introduced.
To measure this, we can use a system like the one shown in the image:

To determine the average velocity, two sensors must be placed to record the passage of an object at a distance $\Delta s$. The time difference in which the object passes in front of each sensor is then recorded as $\Delta t$. The average velocity is determined by dividing the distance traveled by the time elapsed.
The equation that describes the mean Speed ($\bar{v}$) with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) is the following:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
It should be noted that the average velocity is an estimate of the actual velocity. The main problem lies in the fact that:
If the velocity changes during the elapsed time, the value of the average velocity can be very different from the average speed.
Additionally, there is a problem with the way the distance traveled is measured, as we work with two positions. This can lead to the situation where:
Since the path traveled is calculated from the difference between two positions, in cases where the movement is reversed during the elapsed time, the initial and final positions can be very similar. This can lead to an average velocity that is approximately zero, despite having traveled a 'long' distance.
Therefore, the key is to:
Determine the velocity in a sufficiently short elapsed time so that its variation is minimal.
(ID 470)
If displacement is graphed as a line between the origin O and point A:

it can be seen that a path has been traveled over a period of time. Therefore, the slope of the graph of path vs elapsed time corresponds to velocity.
If the slope is steeper, it means that a path is covered in less time, which corresponds to a higher velocity.
If the slope is flatter, it means that a path is covered in more time, which corresponds to a lower velocity.
(ID 2239)
A second type of case is horizontal segments in the distance vs time graph:

If we observe segment AB, we will notice that despite the elapsed time, the distance has not changed. This means that the object is at rest. Therefore, horizontal segments, which correspond to zero slope, correspond to periods when the velocity is zero.
(ID 2241)
For the case of constant velocity and initial time, the position can be calculated using the values the position ($s$), the starting position ($s_0$), the constant velocity ($v_0$), the time ($t$), and the start Time ($t_0$) with the following equation:
| $ s = s_0 + v_0 ( t - t_0 )$ |
which corresponds to a straight line with:
• a slope equal to the constant velocity ($v_0$)
• a y-intercept at the starting position ($s_0$) for the start Time ($t_0$)
as illustrated below:

(ID 2243)
When a segment on a graph has a negative slope, as shown below:

it represents a situation in which the object returned from position B to C, which is a distance of zero from the origin. In other words, negative slopes correspond to traveling in the opposite direction, not moving away but getting closer to the origin.
(ID 2245)
When a body is said to be "at rest", it means that it is at rest relative to our reference frame or coordinate system. However, this "rest" is entirely relative, meaning that from a body that moves relative to our system, the body at "rest" is also in motion.
In this sense, there is no such thing as an "absolute rest", it only exists as something relative to a particular reference frame. Therefore, in general, all velocity measurements are relative to a particular reference frame.
For example, if a body appears to move very slowly, it only means that its velocity is very similar to the velocity of the reference frame in which the slow movement is observed.
(ID 4405)
The base model relates the position ($s$), measured from an origin the starting position ($s_0$), resulting in ERROR:6025.1, and the time ($t$), measured from an origin the start Time ($t_0$), resulting in the time elapsed ($\Delta t$). From these differences, the mean Speed ($\bar{v}$) is defined, which, if assumed constant, is equal to the constant velocity ($v_0$).
The base relationship of the model is the straight line that associates the central variables of the model:

With this, the network structure of the model is:
(ID 15378)
We can calculate the distance traveled in a time ($\Delta s$) from the starting position ($s_0$) and the position ($s$) using the following equation:
| $ \Delta s = s_2 - s_1 $ |
(ID 4352)
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
| $ \Delta t \equiv t - t_0 $ |
(ID 4353)
The mean Speed ($\bar{v}$) can be calculated from the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) using:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
(ID 3152)
If the speed is constant, the velocity will be equal to the initial Speed ($v_0$). In this case, the distance traveled as a function of time can be calculated using the difference between the position ($s$) and the starting position ($s_0$), divided by the difference between the time ($t$) and the start Time ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )$ |
The corresponding equation defines a straight line in space-time.
(ID 3154)
ID:(608, 0)
