Aceleração instantânea
Descrição 
Variáveis
Cálculos
Cálculos
Equações
Como um vetor pode ser expresso como um conjunto de suas diferentes componentes
$\vec{v}=(v_x,v_y,v_z)$
sua derivada pode ser expressa como a derivada de cada uma de suas componentes
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
em geral, a velocidade instant nea em mais de uma dimens o
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
(ID 3155)
Se considerarmos a diferen a em la velocidade ($v$) nos tempos $t+\Delta t$ e $t$:
$\Delta v = v(t+\Delta t)-v(t)$
e tomarmos $\Delta t$ como o tempo decorrido ($\Delta t$), ent o, no limite de tempos infinitesimalmente curtos:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Esta ltima express o corresponde derivada da fun o la velocidade ($v$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
que, por sua vez, a inclina o da representa o gr fica dessa fun o em o tempo ($t$).
(ID 4356)
Se integrarmos a defini o de la aceleração instantânea ($a$) em o tempo ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
isso significa que, para um intervalo de tempo $dt$, a dist ncia percorrida
$dv = a dt$
Se considerarmos $N$ intervalos $dt_i$ com acelera es $a_i$, a varia o total na velocidade ser
$v - v_0 = \displaystyle\sum_i a_i dt_i$
Se considerarmos a curva de acelera o-tempo, os elementos $a_i dt_i$ correspondem a ret ngulos com altura $a_i$ e largura $dt_i$. A soma, portanto, corresponde rea sob a curva de acelera o-tempo. Portanto, a soma pode ser expressa como uma integral:
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
(ID 10307)
Dado que la aceleração instantânea ($a$) a derivada de la velocidade ($v$) em rela o a o tempo ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
e la velocidade ($v$) a derivada de la posição ($s$) em rela o a o tempo ($t$),
| $ v =\displaystyle\frac{ d s }{ d t }$ |
temos que
$a=\displaystyle\frac{dv}{dt}=\displaystyle\frac{d}{dt}\displaystyle\frac{ds}{dt}=\displaystyle\frac{d^2s}{dt^2}$
portanto,
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
(ID 12572)
Exemplos
Por um lado, importante diferenciar entre o caso mais simples, unidimensional, e aquele de mais de uma dimens o. Para ambos os casos, a derivada de la velocidade ($v$) em rela o a o tempo ($t$), que corresponde inclina o da curva de la velocidade ($v$), igual a la aceleração instantânea ($a$). Da mesma forma, a derivada de la velocidade (vector) ($\vec{v}$) em rela o a o tempo ($t$), que corresponde a la velocidade (vector) ($\vec{v}$).
(ID 15398)
A acelera o definida como a varia o da velocidade por tempo. No entanto, esse conceito se resume a uma acelera o m dia que existe durante o intervalo de tempo considerado.
A limita o da acelera o m dia refletida no fato de que um processo que inclui um processo de acelera o seguido por desacelera o at parar ter uma acelera o m dia de zero. Assim, em m dia, n o haveria acelera o e, se estiver parado, n o se mover , enquanto na verdade avan a tanto na fase de acelera o quanto na de frenagem.
Se desejamos conhecer a acelera o em cada instante, devemos considerar um intervalo de tempo suficientemente pequeno para que durante esse tempo a acelera o possa ser considerada aproximadamente constante. Dessa forma, a acelera o m dia estimada dessa maneira equivale acelera o existente no momento considerado.
Portanto, falamos em 'acelera o instant nea' para nos referirmos acelera o em um determinado momento.
(ID 11352)
Se tomarmos o tempo decorrido ($\Delta t$) e observarmos um objeto em movimento com velocidade la velocidade ($v$), e depois observarmos o mesmo objeto em um momento posterior $t+\Delta t$ com velocidade $v(t+\Delta t)$, podemos estimar sua acelera o como a mudan a na velocidade durante o tempo decorrido ($\Delta t$):
$a\sim\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}$
medida que o valor de $\Delta t$ diminui, essa express o para a acelera o se aproxima da taxa de varia o instant nea da velocidade no momento $t$, ou seja, a inclina o da reta tangente curva de velocidade naquele ponto:

Isso generaliza o conceito de la aceleração instantânea ($a$) para o caso de la aceleração constante ($a_0$), como visto anteriormente, expresso como a derivada de la velocidade ($v$) em rela o a o tempo ($t$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
(ID 11353)
Se algu m observa que la velocidade ($v$) igual a la distância percorrida em um tempo ($\Delta s$) por o tempo decorrido ($\Delta t$), isso indica que o caminho dado por:
$\Delta s = v\Delta t$
Como o produto $v\Delta t$ representa a rea sob a curva de velocidade versus tempo, que tamb m igual ao caminho percorrido:

Essa rea tamb m pode ser calculada com a integral da fun o correspondente. Portanto, a integral da acelera o entre o tempo inicial ($t_0$) e o tempo ($t$) corresponde mudan a na velocidade entre a velocidade inicial la velocidade inicial ($v_0$) e la velocidade ($v$):
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
(ID 2252)
La aceleração instantânea ($a$) igual derivada de la velocidade ($v$) em rela o a o tempo ($t$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
E j que la velocidade ($v$) a derivada de la posição ($s$) em rela o a o tempo ($t$):
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Portanto, la aceleração instantânea ($a$) a segunda derivada de la posição ($s$) em rela o a o tempo ($t$),
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
o que corresponde curvatura da curva la posição ($s$) em fun o de o tempo ($t$):
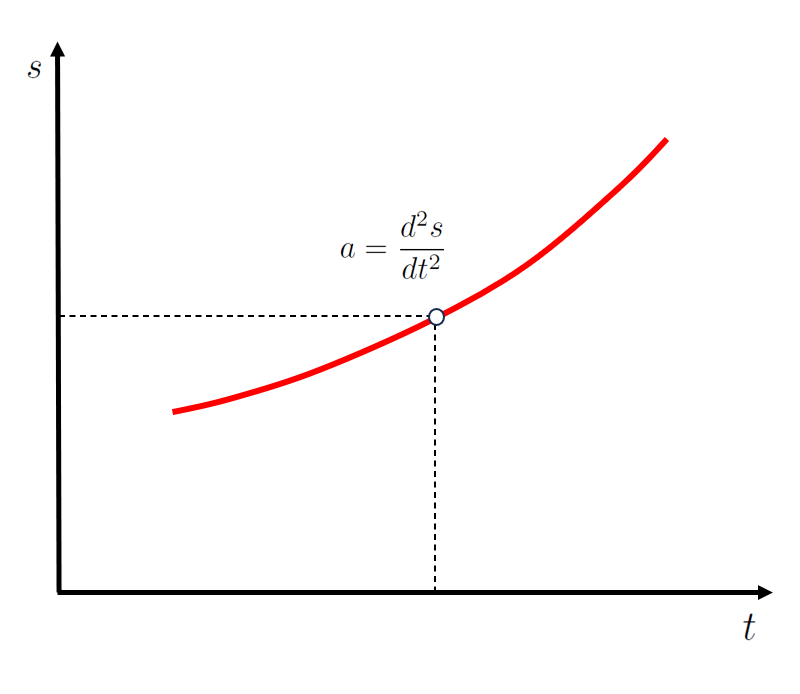
(ID 11354)
No caso de uma dimens o, la aceleração instantânea ($a$) est relacionada com la velocidade ($v$) atrav s de sua derivada em o tempo ($t$), enquanto a integral de la aceleração instantânea ($a$) no intervalo de o tempo ($t$) a o tempo inicial ($t_0$) fornece la velocidade ($v$) a partir de la velocidade inicial ($v_0$). Em um contexto mais geral, em mais de uma dimens o, a fun o de la velocidade (vector) ($\vec{v}$) pode ser derivada em o tempo ($t$), resultando em la velocidade (vector) ($\vec{v}$).
(ID 15401)
ID:(1433, 0)
