Usuario:
Distancia recorrida
Ecuación
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuación:
 $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Tiempo transcurrido
Ecuación
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duración se determina restando el tiempo inicial a el tiempo final:
| $ \Delta t \equiv t - t_0 $ |
ID:(4353, 0)
Variación de la velocidad
Ecuación
La aceleración se define como la variación de la velocidad por unidad de tiempo.
Por lo tanto, es necesario establecer la diferencia de velocidad ($\Delta v$) en función de la velocidad ($v$) y la velocidad inicial ($v_0$) de la siguiente manera:
| $ \Delta v \equiv v - v_0 $ |
ID:(4355, 0)
Velocidad media
Ecuación
La velocidad media ($\bar{v}$) se puede calcular de la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) mediante:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(3152, 0)
Velocidad media al caminar
Ecuación
La cadera se desplaza a una velocidad aproximadamente constante. Esta se puede determinar calculando la velocidad media con que la persona recorre la distancia
| $ v =\displaystyle\frac{ L }{ t }$ |
ID:(3699, 0)
Velocidad instantánea en una dimensión
Ecuación
La velocidad ($v$) instantánea, determinada por la relación entre la distancia infinitesimal recorrida ($ds$) y la variación infinitesimal del tiempo ($dt$), proporciona una estimación más precisa de la velocidad real en cualquier momento de el tiempo ($t$), en comparación con la velocidad media ($\bar{v}$), que se calcula a partir de la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) mediante la ecuación:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Esto se logra mediante la derivada de la posición con respecto al tiempo, es decir:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Si consideramos el camino recorrido como la diferencia de posición entre el tiempo $t+\Delta t$ y el tiempo $t$:
$\Delta s = s(t+\Delta t)-s(t)$
y tomamos $\Delta t$ como el tiempo transcurrido, entonces en el límite de tiempos infinitesimalmente cortos, la velocidad media puede expresarse como:
$v_m=\displaystyle\frac{\Delta s}{\Delta t}=\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}=\displaystyle\frac{ds}{dt}$
Esta última expresión corresponde a la derivada de la función de posición $s(t)$:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
que, a su vez, es la pendiente de la representación gráfica de dicha función en función del tiempo.
De esta manera, la velocidad instantánea la velocidad ($v$) de la posición ($s$) se conoce en cualquier instante de el tiempo ($t$) con mayor precisión.
ID:(3153, 0)
Velocidad instantánea en más dimensiones
Ecuación
En general, la velocidad ($v$) debe entenderse como una entidad tridimensional, es decir, un vector la velocidad (vector) ($\vec{v}$). Cada componente se puede definir como la derivada de la posición ($s$) en el tiempo ($t$):
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Por de puede con la derivada en el tiempo ($t$) de la posición (vector) ($\vec{s}$) como la velocidad (vector) ($\vec{v}$):
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
Al ser un vector, la velocidad se puede expresar como una arreglo de sus diferentes componentes:
$\vec{v}=\begin{pmatrix}v_x\v_y\v_z\end{pmatrix}$
y su derivada se puede expresar como la derivada de cada una de sus componentes:
$\displaystyle\frac{d\vec{v}}{dt}=\begin{pmatrix}\displaystyle\frac{d v_x}{dt}\displaystyle\frac{d v_y}{dt}\displaystyle\frac{d v_z}{dt}\end{pmatrix}=\begin{pmatrix}a_x\a_y\a_z\end{pmatrix}=\vec{a}$
Así, en general, la velocidad instantánea en más de una dimensión es un vector con componentes en cada una de las direcciones:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
ID:(4354, 0)
Evolución de la velocidad
Concepto
En el caso de un movimiento en dos etapas, la primera etapa se puede describir mediante una función que involucra los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), la velocidad inicial ($v_0$) y la velocidad primera etapa ($v_1$), representada por una recta con pendiente de la aceleración durante la primera etapa ($a_1$):
Para la segunda etapa, definida por los puntos la velocidad primera etapa ($v_1$), la velocidad segunda etapa ($v_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se emplea una segunda recta con pendiente de la aceleración durante la segunda etapa ($a_2$):
que se representa como:
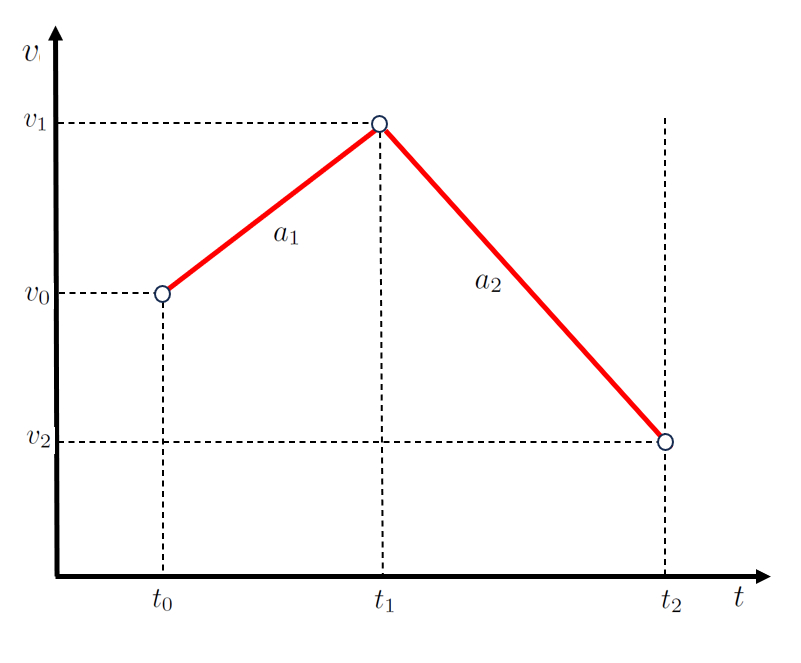
ID:(4357, 0)
Velocidad máxima del pie
Ecuación
Cuando el pie adelanta para posicionarse en una posición adelantada lo debe de hacer a una velocidad mayor a la que se desplaza el tronco del cuerpo.
Por ello la velocidad del pie llega a un máximo que es igual a la suma de la velocidad media del cuerpo
| $ v_t = v + v_r $ |
ID:(3701, 0)
Posición con velocidad constante
Ecuación
Si la velocidad es igual a una velocidad inicial ($v_0$), entonces la velocidad media ($\bar{v}$) es igual a esta:
| $ \bar{v} = v_0$ |
.
En este caso, el camino recorrido en función del tiempo puede ser calculado utilizando la diferencia entre la posición ($s$) y la posición inicial ($s_0$), dividida por la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )$ |
En el caso de que una velocidad inicial ($v_0$) sea igual a la velocidad media ($\bar{v}$):
| $ \bar{v} = v_0$ |
Por lo tanto, con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuación de la velocidad media:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = v_m = displaystylefrac{Delta s}{Delta t} = displaystylefrac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
La ecuación correspondiente define una recta en el espacio-tiempo.
ID:(3154, 0)
Aceleración media
Ecuación
La proporción en la que la variación de la velocidad a lo largo del tiempo se define como la aceleración media ($\bar{a}$). Para medirla, es necesario observar la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$).
Un método común para medir la aceleración media consiste en utilizar una lámpara estroboscópica que ilumina el objeto en intervalos definidos. Al tomar una fotografía, se puede determinar la distancia recorrida por el objeto en ese tiempo. Al calcular dos velocidades consecutivas, se puede determinar su variación y, con el tiempo transcurrido entre las fotos, la aceleración media.
La ecuación que describe la aceleración media es la siguiente:
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
La definición de la aceleración media ($\bar{a}$) se considera como la relación entre la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$). Es decir,
| $ \Delta v \equiv v - v_0 $ |
y
| $ \Delta t \equiv t - t_0 $ |
Se define la relación entre ambos como la aceleración centrifuga ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
en dicho intervalo de tiempo.
Es importante tener en cuenta que la aceleración media es una estimación de la aceleración real.
El problema principal radica en que si la aceleración varía durante el tiempo transcurrido, el valor de la aceleración media puede diferir en gran medida de la aceleración promedio
.
Por lo tanto, la clave es
Determinar la aceleración en un período de tiempo suficientemente corto para minimizar la variación.
ID:(3678, 0)
Aceleración instantánea en más dimensiones
Ecuación
En general, la velocidad debe entenderse como un vector tridimensional. Es decir, su la posición ($s$) requiere ser descrita por un vector una posición (vector) ($\vec{s}$), para el cual se puede definir cada componente la velocidad ($v$) como se muestra en la siguiente ecuación:
| $ a =\displaystyle\frac{ dv }{ dt }$ |
Esto permite generalizar la velocidad (vector) ($\vec{v}$) de la siguiente manera:
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
Como un vector se puede expresar como un arreglo de sus diferentes componentes
$\vec{v}=(v_x,v_y,v_z)$
su derivada se puede expresar como la derivada de cada una de sus componentes
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
se tiene que en general la velocidad instantanea en mas de una dimensión es
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
ID:(3155, 0)
Aceleración instantánea en una dimensión
Ecuación
La variable la aceleración media ($\bar{a}$), calculada como el cambio en la diferencia de velocidad ($\Delta v$) dividido por el intervalo de el tiempo transcurrido ($\Delta t$) mediante
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
es una aproximación de la aceleración real, que tiende a distorsionarse cuando la aceleración fluctúa durante el intervalo de tiempo. Por lo tanto, se introduce el concepto de la aceleración instantanea ($a$) determinado en un intervalo de tiempo muy pequeño. En este caso, nos referimos a un intervalo de tiempo infinitesimalmente pequeño y la variación de la velocidad en el tiempo se reduce a la derivada de la velocidad ($v$) respecto a el tiempo ($t$):
| $ a =\displaystyle\frac{ dv }{ dt }$ |
Si consideramos la diferencia de la velocidad ($v$) en los tiempos $t+\Delta t$ y $t$:
$\Delta v = v(t+\Delta t)-v(t)$
y tomamos $\Delta t$ como el tiempo transcurrido ($\Delta t$), entonces en el límite de tiempos infinitesimalmente cortos:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Esta última expresión corresponde a la derivada de la función la velocidad ($v$):
| $ a =\displaystyle\frac{ dv }{ dt }$ |
la cual, a su vez, es la pendiente de la representación gráfica de dicha función en el tiempo ($t$).
lo que corresponde a la derivada de la velocidad.
ID:(4356, 0)
Velocidad con aceleración constante
Ecuación
Si la aceleración constante ($a_0$), entonces la aceleración media ($\bar{a}$) es igual al valor de la aceleración, es decir,
| $ a_0 = \bar{a} $ |
.
En este caso, la velocidad ($v$) como función de el tiempo ($t$) se puede calcular recordando que está asociada con la diferencia entre la velocidad ($v$) y la velocidad inicial ($v_0$), así como el tiempo ($t$) y el tiempo inicial ($t_0$).
| $ v = v_0 + a_0 ( t - t_0 )$ |
En el caso de que la aceleración constante ($a_0$) sea igual a la aceleración media ($\bar{a}$), será igual a
| $ a_0 = \bar{a} $ |
.
Por lo tanto, considerando la diferencia de velocidad ($\Delta v$)
| $ \Delta v \equiv v - v_0 $ |
y el tiempo transcurrido ($\Delta t$)
| $ \Delta t \equiv t - t_0 $ |
,
la ecuación de la aceleración constante ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
se puede escribir como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
y al despejar, se obtiene
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
De esta manera, la ecuación representa una línea recta en el espacio de velocidad-tiempo.
ID:(3156, 0)
Camino con aceleración constante
Ecuación
En el caso de que una aceleración constante ($a_0$), la variable la velocidad ($v$) varía de forma lineal con respecto a el tiempo ($t$), utilizando la velocidad inicial ($v_0$) y el tiempo inicial ($t_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
Así, el área bajo esta recta se puede calcular, lo que nos proporciona la distancia recorrida en un tiempo ($\Delta s$). Al combinar esto con la posición inicial ($s_0$), podemos calcular la posición ($s$), lo que resulta en:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
En el caso de la aceleración constante ($a_0$), la velocidad ($v$) en función de el tiempo ($t$) es una recta que pasa por el tiempo inicial ($t_0$) y la velocidad inicial ($v_0$), definida por la ecuación:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Dado que la distancia recorrida en un tiempo ($\Delta s$) representa el área bajo la curva velocidad-tiempo, podemos sumar las contribuciones del rectángulo:
$v_0(t-t_0)$
y el triángulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Para obtener la distancia recorrida en un tiempo ($\Delta s$) con la posición ($s$) y la posición inicial ($s_0$), resultando en:
| $ \Delta s \equiv s - s_0 $ |
Por lo tanto:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Esto corresponde a la forma general de una parábola.
ID:(3157, 0)
Camino con aceleración constante y tiempo inicial cero
Ecuación
En el caso de que se asuma que la aceleración inicial es constante y tiempo inicial nulo la ecuación de la posición
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
En el caso de que se asuma que el tiempo inicial es nulo\\n\\n
$t_0=0$
la ecuación de la posición
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
ID:(4360, 0)
Camino de aceleración/frenado en función de la velocidad
Ecuación
En el caso de una aceleración constante, podemos calcular la posición ($s$) a partir de la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) según la ecuación:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Esto nos permite calcular la relación entre la distancia de aceleración/frenado y el cambio de velocidad:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
Si despejamos las ecuaciones para el tiempo ($t$) y el tiempo inicial ($t_0$) en la ecuación de la velocidad ($v$), que depende de la velocidad inicial ($v_0$) y la aceleración constante ($a_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
obtenemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Y al sustituir esto en la ecuación de la posición ($s$) con la posición inicial ($s_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
obtenemos una expresión para el camino recorrido en función de la velocidad:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
ID:(3158, 0)
Velocidad con aceleración gravitacional (sistema hacia abajo)
Ecuación
Si un objeto se describe en un sistema de coordenadas en el que el eje z apunta \"hacia abajo\" (hacia el suelo), la aceleración a la que se expone es igual a la aceleración gravitacional, que se define como positiva:
$a = g > 0$
Debido a que la aceleración es constante, la velocidad evoluciona de forma lineal, como se muestra en la siguiente ecuación:
| $$ |
Por lo tanto, en este caso se reduce a la siguiente ecuación:
| $ v_{pg} = v_0 + g t $ |
ID:(4359, 0)
Velocidad con aceleración gravitacional (sistema hacia arriba)
Ecuación
Cuando se describe el movimiento de un objeto en un sistema de coordenadas en el que el eje z apunta hacia arriba (hacia el cielo), la aceleración experimentada por el objeto es igual a la aceleración gravitatoria definida como negativa, dada por
$a = -g < 0$
.
Como la aceleración es constante, la velocidad del objeto cambiará linealmente, como se describe en la ecuación
| $$ |
,
que se simplifica a
| $ v_{ng} = v_0 - g t $ |
en este caso.
ID:(4358, 0)
Límite paso de caminar a correr
Ecuación
La aceleración centrifuga depende de la velocidad tangencial
Si la aceleración centrifuga supera la aceleración gravitacional
el cuerpo se comienza a elevar. La elevación involucra un cambio en la forma como nos desplazamos, es decir pasamos del modo caminar al modo correr. El limite en que ambas aceleraciones son iguales nos da una velocidad crítica:
que al despejar es
Esto significa que a baja velocidad caminamos, pero al aumentar la velocidad si llegamos a superar el valor crítico
ID:(4736, 0)