Benützer:
Entwicklung der Geschwindigkeit
Beschreibung
Im Fall einer zweistufigen Bewegung kann die erste Stufe durch eine Funktion beschrieben werden, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), die Anfangsgeschwindigkeit ($v_0$) und die Geschwindigkeit der ersten Stufe ($v_1$) einbezieht und durch eine Gerade mit einer Steigung von die Beschleunigung während der ersten Stufe ($a_1$) dargestellt wird:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Für die zweite Stufe, definiert durch die Punkte die Geschwindigkeit der ersten Stufe ($v_1$), die Geschwindigkeit der zweiten Stufe ($v_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$), wird eine zweite Gerade mit einer Steigung von die Beschleunigung während der zweiten Stufe ($a_2$) verwendet:
| $ v = v_0 + a_0 ( t - t_0 )$ |
die wie folgt dargestellt wird:
ID:(4357, 0)
Elevarse y Correr
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Wenn wir den zur ckgelegten Weg als die Differenz der Positionen zwischen der Zeit $t+\Delta t$ und der Zeit $t$ betrachten:
$\Delta s = s(t+\Delta t)-s(t)$
und $\Delta t$ als die vergangene Zeit nehmen, dann kann die durchschnittliche Geschwindigkeit im Grenzwert infinitesimal kurzer Zeiten ausgedr ckt werden als:
$v_m=\displaystyle\frac{\Delta s}{\Delta t}=\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}=\displaystyle\frac{ds}{dt}$
Dieser letzte Ausdruck entspricht der Ableitung der Positionsxadfunktion $s(t)$:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
die wiederum die Steigung der graphischen Darstellung dieser Funktion ber der Zeit ist.
(ID 3153)
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s = s - s_0 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung f r die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Da ein Vektor als eine Anordnung seiner verschiedenen Komponenten ausgedr ckt werden kann,
$\vec{v}=(v_x,v_y,v_z)$
kann seine Ableitung als Ableitung jeder seiner Komponenten ausgedr ckt werden:
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
Im Allgemeinen gilt, dass die instantane Geschwindigkeit in mehr als einer Dimension
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
(ID 3155)
Im Falle, dass die konstante Beschleunigung ($a_0$) gleich die Mittlere Beschleunigung ($\bar{a}$) ist, wird es gleich
| $ a_0 = \bar{a} $ |
.
Deshalb, wenn wir die Geschwindigkeit Unterschied ($\Delta v$) als
| $ dv \equiv v - v_0 $ |
und der Abgelaufene Zeit ($\Delta t$) als
| $ \Delta t \equiv t - t_0 $ |
betrachten, kann die Gleichung f r die konstante Beschleunigung ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
als
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
geschrieben werden, und durch Umstellen erhalten wir
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Im Fall von die konstante Beschleunigung ($a_0$) ist die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) eine Gerade, die durch der Startzeit ($t_0$) und die Anfangsgeschwindigkeit ($v_0$) verl uft und durch die Gleichung definiert ist:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Da die Zurückgelegte Strecke in einer Zeit ($\Delta s$) den Bereich unter der Geschwindigkeits-Zeit-Kurve darstellt, k nnen wir die Beitr ge des Rechtecks summieren:
$v_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Um die Zurückgelegte Strecke in einer Zeit ($\Delta s$) mit die Position ($s$) und die Ausgangsstellung ($s_0$) zu erhalten, ergibt sich:
| $ \Delta s = s - s_0 $ |
Daraus folgt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Wenn wir die Gleichungen f r der Zeit ($t$) und der Startzeit ($t_0$) in die Gleichung f r die Geschwindigkeit ($v$) aufl sen, die von die Anfangsgeschwindigkeit ($v_0$) und die konstante Beschleunigung ($a_0$) abh ngt:
| $ v = v_0 + a_0 ( t - t_0 )$ |
erhalten wir:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Dann, wenn wir diesen Ausdruck in die Gleichung f r die Position ($s$) mit die Ausgangsstellung ($s_0$) einsetzen:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
erhalten wir einen Ausdruck f r den zur ckgelegten Weg in Abh ngigkeit von der Geschwindigkeit:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
Die Definition von die Mittlere Beschleunigung ($\bar{a}$) wird als die Beziehung zwischen die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) betrachtet. Das hei t,
| $ dv \equiv v - v_0 $ |
und
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Kreiselbeschleunigung ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
innerhalb dieses Zeitintervalls definiert.
(ID 3678)
(ID 3701)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Da die Geschwindigkeit ein Vektor ist, kann sie als ein Array ihrer verschiedenen Komponenten ausgedr ckt werden:
$\vec{v}=\begin{pmatrix}v_x\v_y\v_z\end{pmatrix}$
Ihre Ableitung kann als die Ableitung jeder ihrer Komponenten ausgedr ckt werden:
$\displaystyle\frac{d\vec{v}}{dt}=\begin{pmatrix}\displaystyle\frac{d v_x}{dt}\displaystyle\frac{d v_y}{dt}\displaystyle\frac{d v_z}{dt}\end{pmatrix}=\begin{pmatrix}a_x\a_y\a_z\end{pmatrix}=\vec{a}$
Daher ist die instantane Geschwindigkeit im Allgemeinen in mehr als einer Dimension ein Vektor mit Komponenten in jeder Richtung:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
(ID 4354)
(ID 4355)
Wenn wir die Differenz von die Geschwindigkeit ($v$) zu den Zeiten $t+\Delta t$ und $t$ betrachten:
$\Delta v = v(t+\Delta t)-v(t)$
und $\Delta t$ als der Abgelaufene Zeit ($\Delta t$) nehmen, dann im Grenzwert von infinitesimal kurzen Zeiten:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Diese letzte Ausdruck entspricht der Ableitung der Funktion die Geschwindigkeit ($v$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
welche wiederum die Steigung der grafischen Darstellung dieser Funktion bei der Zeit ($t$) ist.
(ID 4356)
En el caso de que se asuma que el tiempo inicial es nulo\\n\\n
$t_0=0$
la ecuaci n de la posici n
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
(ID 4360)
Beispiele
Um die Bewegung eines Objekts zu beschreiben, m ssen wir der Abgelaufene Zeit ($\Delta t$) berechnen. Diese Gr e wird durch Messung von der Startzeit ($t_0$) und der der Zeit ($t$) dieser Bewegung erhalten. Die Dauer wird bestimmt, indem die Anfangszeit von der Endzeit subtrahiert wird:
| $ \Delta t \equiv t - t_0 $ |
(ID 4353)
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) kann aus die Ausgangsstellung ($s_0$) und die Position ($s$) mit folgender Gleichung berechnet werden:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Beschleunigung entspricht der nderung der Geschwindigkeit pro Zeiteinheit.
Deshalb ist es notwendig, die Geschwindigkeit Unterschied ($\Delta v$) in Abh ngigkeit von die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) wie folgt zu definieren:
| $ dv \equiv v - v_0 $ |
(ID 4355)
Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
(ID 3152)
$v=\displaystyle\frac{L}{t}$
(ID 3699)
Die momentane ERROR:6029,0, bestimmt durch die Beziehung zwischen die Infinitesimal zurückgelegte Strecke ($ds$) und die Infinitesimale Variation of Time ($dt$), liefert eine genauere Sch tzung der tats chlichen Geschwindigkeit zu jedem Zeitpunkt von der Zeit ($t$), im Vergleich zu die Mittlere Geschwindigkeit ($\bar{v}$), die aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) mit der Gleichung berechnet wird:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Dies wird durch die Ableitung der Position nach der Zeit erreicht, d.h.:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Daher ist die momentane Geschwindigkeit die Geschwindigkeit ($v$) von die Position ($s$) zu jedem Zeitpunkt von der Zeit ($t$) mit gr erer Genauigkeit bekannt.
(ID 3153)
Im Allgemeinen muss die Geschwindigkeit als eine dreidimensionale Einheit verstanden werden, also als Vektor. Ihre Position wird durch einen Positionsvektor
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Dies erm glicht die Verallgemeinerung der Geschwindigkeit:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
(ID 4354)
Im Fall einer zweistufigen Bewegung kann die erste Stufe durch eine Funktion beschrieben werden, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), die Anfangsgeschwindigkeit ($v_0$) und die Geschwindigkeit der ersten Stufe ($v_1$) einbezieht und durch eine Gerade mit einer Steigung von die Beschleunigung während der ersten Stufe ($a_1$) dargestellt wird:
| $ v = v_0 + a_0 ( t - t_0 )$ |
F r die zweite Stufe, definiert durch die Punkte die Geschwindigkeit der ersten Stufe ($v_1$), die Geschwindigkeit der zweiten Stufe ($v_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$), wird eine zweite Gerade mit einer Steigung von die Beschleunigung während der zweiten Stufe ($a_2$) verwendet:
| $ v = v_0 + a_0 ( t - t_0 )$ |
die wie folgt dargestellt wird:
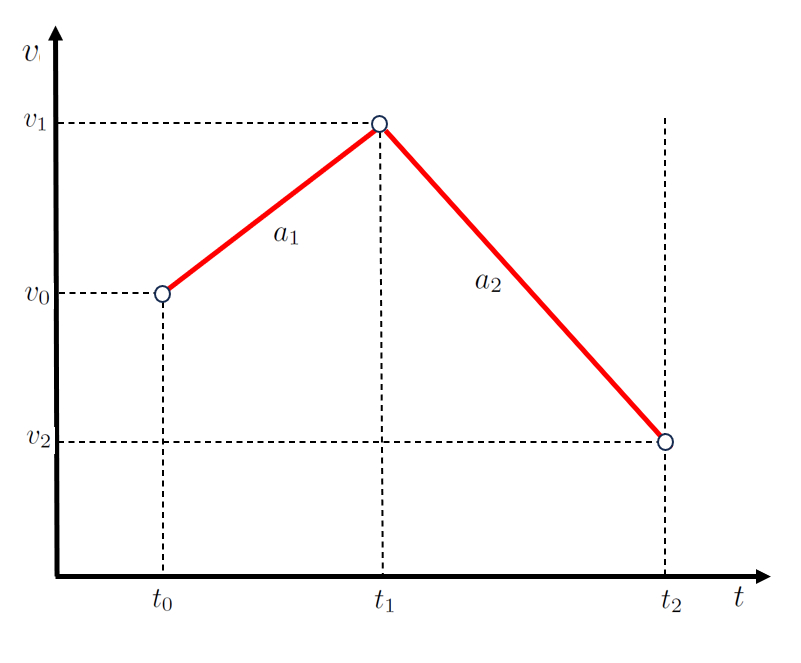
(ID 4357)
$v_t=v+v_r$
(ID 3701)
Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zur ckgelegte Weg in Abh ngigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:
| $ s = s_0 + v_0 ( t - t_0 )$ |
Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.
(ID 3154)
Das Verh ltnis, in dem die Geschwindigkeits nderung im Laufe der Zeit definiert ist, wird als die Mittlere Beschleunigung ($\bar{a}$) bezeichnet. Um es zu messen, ist es notwendig, die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) zu beobachten.
Eine g ngige Methode zur Messung der durchschnittlichen Beschleunigung besteht darin, eine Stroboskoplampe zu verwenden, die das Objekt in definierten Intervallen beleuchtet. Durch Aufnahme eines Fotos kann man die Strecke bestimmen, die das Objekt in dieser Zeit zur ckgelegt hat. Durch Berechnung von zwei aufeinanderfolgenden Geschwindigkeiten kann man ihre nderung bestimmen und mit der verstrichenen Zeit zwischen den Fotos die durchschnittliche Beschleunigung berechnen.
Die Gleichung f r die durchschnittliche Beschleunigung lautet:
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
Es ist wichtig zu beachten, dass die durchschnittliche Beschleunigung eine Sch tzung der tats chlichen Beschleunigung darstellt.
Das Hauptproblem besteht darin, dass, wenn sich die Beschleunigung w hrend der verstrichenen Zeit ndert, der Wert der durchschnittlichen Beschleunigung stark von der mittleren Beschleunigung abweichen kann.
Daher
Der Schl ssel ist die Beschleunigung ber einen ausreichend kurzen Zeitraum zu bestimmen, um die Variation zu minimieren.
(ID 3678)
Im Allgemeinen sollte die Geschwindigkeit als ein dreidimensionaler Vektor verstanden werden. Das hei t, ihre die Position ($s$) muss durch einen Vektor eine Posición (Vektor) ($\vec{s}$) beschrieben werden, f r den jede Komponente die Geschwindigkeit ($v$) definiert werden kann, wie in der folgenden Gleichung gezeigt:
| $ a =\displaystyle\frac{ d v }{ d t }$ |
Dies erm glicht eine Verallgemeinerung von die Geschwindigkeit (Vektor) ($\vec{v}$) wie folgt:
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
(ID 3155)
Die Variable die Mittlere Beschleunigung ($\bar{a}$), berechnet als nderung in die Geschwindigkeit Unterschied ($\Delta v$) geteilt durch das Intervall von der Abgelaufene Zeit ($\Delta t$) mittels
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
ist eine N herung der tats chlichen Beschleunigung, die dazu neigt, sich zu verzerren, wenn die Beschleunigung w hrend des Zeitintervalls schwankt. Daher wird das Konzept von die Augenblickliche Beschleunigung ($a$) eingef hrt, das ber ein sehr kleines Zeitintervall bestimmt wird. In diesem Fall beziehen wir uns auf ein unendlich kleines Zeitintervall, und die Geschwindigkeits nderung ber die Zeit reduziert sich auf die Ableitung von die Geschwindigkeit ($v$) nach der Zeit ($t$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
was der Ableitung der Geschwindigkeit entspricht.
(ID 4356)
Wenn die konstante Beschleunigung ($a_0$) ist, dann ist die Mittlere Beschleunigung ($\bar{a}$) gleich dem Wert der Beschleunigung, das hei t,
| $ a_0 = \bar{a} $ |
.
In diesem Fall kann die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) berechnet werden, indem ber cksichtigt wird, dass sie mit der Differenz zwischen die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) sowie der Zeit ($t$) und der Startzeit ($t_0$) verbunden ist.
| $ v = v_0 + a_0 ( t - t_0 )$ |
Diese Gleichung repr sentiert somit eine Gerade im Geschwindigkeits-Zeit-Raum.
(ID 3156)
Im Fall von ERROR:5297.1 variiert die Geschwindigkeit ($v$) linear mit der Zeit ($t$), unter Verwendung von die Anfangsgeschwindigkeit ($v_0$) und der Startzeit ($t_0$):
| $ v = v_0 + a_0 ( t - t_0 )$ |
Daher kann die Fl che unter dieser Linie berechnet werden, was zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$) f hrt. In Kombination mit die Ausgangsstellung ($s_0$) k nnen wir die Position ($s$) berechnen, was zu folgendem Ergebnis f hrt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Dies entspricht der allgemeinen Form einer Parabel.
(ID 3157)
En el caso de que se asuma que la aceleraci n inicial es constante y tiempo inicial nulo la ecuaci n de la posici n
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
(ID 4360)
Im Falle einer konstanten Beschleunigung k nnen wir die Position ($s$) aus die Ausgangsstellung ($s_0$), die Anfangsgeschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mit der Gleichung berechnen:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
Dies erm glicht es uns, die Beziehung zwischen der w hrend der Beschleunigung/Verz gerung zur ckgelegten Strecke und der nderung der Geschwindigkeit zu bestimmen:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
Wenn ein Objekt in einem Koordinatensystem beschrieben wird, bei dem die z-Achse \"nach unten\" (Richtung Boden) zeigt, ist die Beschleunigung, der es ausgesetzt ist, gleich der Gravitationsbeschleunigung, die als positiv definiert ist:
$a = g > 0$
Da die Beschleunigung konstant ist, wird sich die Geschwindigkeit linear entwickeln, wie in der folgenden Gleichung dargestellt:
| $$ |
Daher kann sie in diesem Fall auf die folgende Gleichung reduziert werden:
| $ v_{pg} = v_0 + g t $ |
(ID 4359)
Wenn die Bewegung eines Objekts in einem Koordinatensystem beschrieben wird, bei dem die z-Achse nach oben (in Richtung Himmel) zeigt, ist die Beschleunigung, der das Objekt ausgesetzt ist, gleich der als negativ definierten Gravitationsbeschleunigung, gegeben durch
$a = -g < 0$
.
Da die Beschleunigung konstant ist, ndert sich die Geschwindigkeit des Objekts linear entsprechend der Gleichung
| $$ |
,
die in diesem Fall zu
| $ v_{ng} = v_0 - g t $ |
vereinfacht wird.
(ID 4358)
(ID 4736)
ID:(317, 0)