Usuario:
Diferencia de ángulos
Ecuación
Para describir la rotación de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotación, que es el ángulo ($\theta$):
 $ \Delta\theta = \theta - \theta_0 $ |
ID:(3680, 0)
Variación de velocidades angulares
Ecuación
La aceleración se define como el cambio en la velocidad angular por unidad de tiempo.
Por lo tanto, la aceleración angular la diferencia de velocidades angulares ($\Delta\omega$) se puede expresar en términos de la velocidad angular la velocidad angular ($\omega$) y el tiempo la velocidad angular inicial ($\omega_0$) de la siguiente manera:
| $ \Delta\omega = \omega - \omega_0 $ |
ID:(3681, 0)
Velocidad angular media
Ecuación
Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en función de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporción entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).
Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:
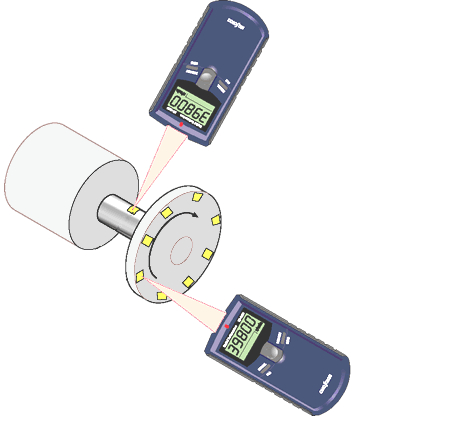
Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ángulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ángulo recorrido por el tiempo transcurrido.
La ecuación que describe la velocidad angular media es:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
La definición de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
| $ \Delta\theta = \theta - \theta_0 $ |
y el tiempo transcurrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relación entre ambos se define como la velocidad angular media ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Cabe destacar que la velocidad media es una estimación de la velocidad angular real. El problema principal es que:
Si la velocidad angular varía durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.
Por lo tanto, la clave es:
Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variación.
ID:(3679, 0)
Velocidad angular instantánea
Ecuación
La la velocidad angular media ($\bar{\omega}$), calculada a partir de una variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$) mediante la ecuación
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
,
es una aproximación de la la velocidad angular instantánea ($\omega$) real que tiende a distorsionarse a medida que la velocidad angular fluctúa durante el intervalo de tiempo. Por lo tanto, se introduce el concepto de la velocidad angular instantánea ($\omega$) determinada en un tiempo muy pequeño. En este caso, hablamos de un intervalo de tiempo infinitesimalmente pequeño.
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
Si consideramos el ángulo recorrido como la variación del angulo ($\Delta\theta$) en el tiempo $t+\Delta t$ y en $t$:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
y usamos el tiempo transcurrido ($\Delta t$), entonces, en el límite de tiempos infinitesimalmente cortos:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
Esta última expresión corresponde a la derivada de la función de ángulo $\theta(t)$, que a su vez es la pendiente de la representación gráfica de dicha función en el tiempo.
que corresponde a la derivada del ángulo.
ID:(3232, 0)
Velocidad tangencial
Ecuación
Si se divide el camino expresado como arco de un circulo se tendrá que con es
| $ \Delta s=r \Delta\theta $ |
por el tiempo transcurrido
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y como la velocidad angular con diferencia de ángulos $rad$, tiempo transcurrido $s$ y velocidad angular media $rad/s$ es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
se tiene con diferencia de ángulos $rad$, tiempo transcurrido $s$ y velocidad angular media $rad/s$ la relación
| $ v_t = r \omega $ |
ID:(10968, 0)
Velocidad angular con aceleración angular constante
Ecuación
Con la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) establece una relación lineal con el tiempo ($t$), que también incorpora las variables la velocidad angular inicial ($\omega_0$) y el tiempo inicial ($t_0$), tal que:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuación:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega - \omega_0 $ |
y el tiempo transcurrido ($\Delta t$) en relación con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuación para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta última, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Esta ecuación representa una recta en el plano de velocidad angular versus tiempo.
ID:(3237, 0)
Aceleración angular media
Ecuación
La proporción en la que la variación de la velocidad angular a lo largo del tiempo se define como la aceleración angular media ($\bar{\alpha}$). Para medirla, es necesario observar la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$).
La ecuación que describe la aceleración angular media ($\bar{\alpha}$) es la siguiente:
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
La aceleración angular media se define como la proporción del ángulo recorrido
| $ \Delta\omega = \omega - \omega_0 $ |
y el tiempo transcurrido
| $ \Delta t \equiv t - t_0 $ |
Esta relación entre ambos se establece como la aceleración angular media
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
durante dicho intervalo de tiempo.
ID:(3234, 0)
Aceleración angular instantánea
Ecuación
Al igual que en la aceleración de traslación, existe el concepto de aceleración angular instantánea, que es la aceleración angular con aceleración angular media $rad/s^2$, diferencia de velocidades angulares $rad/s$ y tiempo transcurrido $s$
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
que existe en un tiempo específico. Esto se calcula en la aproximación de intervalos de tiempo muy pequeños $(\Delta t\rightarrow 0)$, es decir
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
donde
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
ID:(3235, 0)
Aceleración y aceleración angular
Ecuación
Si dividimos la relación entre la velocidad media ($\bar{v}$), el radio ($r$) y la velocidad angular media ($\bar{\omega}$), expresada en la siguiente ecuación:
| $ v = r \omega $ |
por el valor de el tiempo transcurrido ($\Delta t$), podemos obtener el factor que nos permite calcular la aceleración angular a lo largo de la órbita:
| $ a = r \alpha$ |
Dado que la aceleración media ($\bar{a}$) es igual a la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$) según
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
y la aceleración angular media ($\bar{\alpha}$) es igual a la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$) conforme a
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Si asumimos que la aceleración angular media ($\bar{\alpha}$) es igual a la aceleración angular constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
y suponiendo que la aceleración media ($\bar{a}$) es igual a la aceleración constante ($a_0$)
| $ a_0 = \bar{a} $ |
entonces se obtiene la siguiente ecuación:
| $ a = r \alpha$ |
ID:(3236, 0)
Angulo para aceleración angular constante
Ecuación
Dado que el desplazamiento total corresponde al área bajo la curva de velocidad angular frente al tiempo, en el caso de una aceleración angular constante ($\alpha_0$), se determina que el desplazamiento el ángulo ($\theta$) con las variables el ángulo inicial ($\theta_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) es el siguiente:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en función de el tiempo ($t$) sigue una relación lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ángulo recorrido es igual al área bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribución del rectángulo:
$\omega_0(t-t_0)$
y el triángulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresión para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Esta expresión corresponde a la forma general de una parábola.
ID:(3682, 0)
Centro de masa
Ecuación
Si observamos un cuerpo que se sostiene desde un punto, veremos que debemos balancearlo cuidadosamente para evitar que ruede en una dirección u otra. De ello se desprende la noción de que existe un punto desde el cual el cuerpo puede ser equilibrado sin rotar.
Este punto se llama el centro de masa.
Para determinar el punto de equilibrio, podemos balancear el objeto a lo largo de cada uno de sus ejes. Al orientarlo de cierta manera y encontrar la posición en la que permanece en equilibrio, identificamos una línea imaginaria sobre la cual se encuentra el centro de masa.
Una vez que se ha determinado una de las coordenadas del centro de masa, se gira el objeto para buscar la siguiente coordenada del centro de masa.
De esta manera, se determina un punto conocido como centro de masa, y se puede calcular mediante:
| $ \vec{r}_{CM} =\displaystyle\frac{\displaystyle\sum_i m_i \vec{r}_i }{\displaystyle\sum_i m_i }$ |
Si tenemos varias masas $m_i$, cada una estará sujeta a una fuerza gravitacional
| $ F_g = m_g g $ |
generando un torque igual a
| $ T = r F $ |
donde $r_i$ es la distancia horizontal de la masa $i$ al punto de apoyo. El torque total será
$T=\displaystyle\sum_iT_i$
Si $r_{CM}$ es la posición del centro de masa, el torque total en torno a este punto
$T_{CM}=\displaystyle\sum_i T_i=\displaystyle\sum_i(r_i-r_{CM})m_ig=0$
debe ser cero. A partir de esta ecuación, podemos resolver para encontrar la posición del centro de masa, obteniendo
| $ \vec{r}_{CM} =\displaystyle\frac{\displaystyle\sum_i m_i \vec{r}_i }{\displaystyle\sum_i m_i }$ |
.
.
ID:(3248, 0)
Momento angular
Ecuación
El momento ($p$) fue definido como el producto de la masa inercial ($m_i$) y la velocidad ($v$), lo cual es igual a:
| $ p = m_i v $ |
El análogo de la velocidad ($v$) en el caso de la rotación es la velocidad angular instantánea ($\omega$), por lo tanto, el equivalente a el momento ($p$) debería ser un el momento Angular ($L$) de la forma:
| $ L = I \omega $ |
.
la masa inercial ($m_i$) se asocia con la inercia en la traslación de un cuerpo, por lo que el momento de inercia ($I$) corresponde a la inercia en la rotación de un cuerpo.
ID:(3251, 0)
Implicancia de la conservación del momento angular
Ecuación
Si el momento angular se mantiene constante
| $L=L_0$ |
se tiene con
| $ L = I \omega $ |
se tiene que variaciones en el momento de inercia es compensado con variaciones en la velocidad angular
| $ I_1 \omega_1 = I_2 \omega_2 $ |
ID:(3600, 0)
Aceleración centrifuga en función de la velocidad angular
Ecuación
Si expresamos la velocidad tangencial en función de la velocidad angular, la aceleración centrífuga se calcula como:
| $ a_c = r \omega ^2$ |
Al ser la aceleración centrífuga igual a
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
con
| $ v = r \omega $ |
podemos concluir que:
| $ a_c = r \omega ^2$ |
ID:(4384, 0)
Aceleración centrifuga y centripeta
Concepto
Si un cuerpo atado a una cuerda de longitud $r$ gira con una velocidad tangencial $v$ y la cuerda es cortada, el cuerpo continuará moviéndose inercialmente en línea recta con velocidad constante $v$.
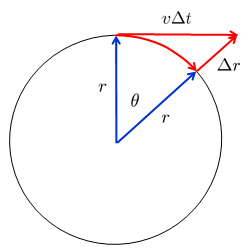
Órbita circula de radio
En un intervalo de tiempo $\Delta t$, el cuerpo habrá recorrido la distancia $v\Delta t$ tangencialmente a su órbita anterior. Desde el punto de vista de un observador en el eje del sistema de rotación, la distancia se calcula utilizando el teorema de Pitágoras, sumando el cuadrado del radio de la órbita con el cuadrado de la distancia recorrida:
$\sqrt{r^2+v^2\Delta t^2}$
ID:(1155, 0)
Inercia y Aceleración Centrifuga
Concepto
Si estudiamos una catapulta, notaremos que la bala primero se mueve a lo largo de la curva que describe la cuchara. Esto sucede porque la cuchara está diseñada para retener la bala. Una vez que se detiene el brazo, la bala continúa en línea recta en forma tangencial al círculo que recorría.
Si un cuerpo no está retenido y viaja con una velocidad tangencial $v$, recorrerá en un tiempo $\Delta t$ la distancia $v\Delta t$, viajando desde el punto B hasta el punto C. Sin embargo, si continúa orbitando, después del tiempo $\Delta t$ llegará al punto D. Si el objeto llega al punto C, desde la perspectiva de un observador en la Tierra, existirá una aceleración que hace que el objeto se aleje de la Tierra (aceleración centrífuga), recorriendo en el tiempo $\Delta t$ la distancia $\Delta r$.
Para un observador en el espacio, un objeto en órbita se encuentra en una caída constante: en lugar de terminar en el punto C, cae en el tiempo $\Delta t$ la distancia $\Delta r$ hasta llegar al punto D. En ambos casos, podemos representar la situación y utilizando el teorema de Pitágoras, podemos ver que se debe cumplir la siguiente ecuación:
$(r+\Delta r)^2=r^2+(v\Delta t)^2$
Si desarrollamos el cuadrado de la ecuación, se reduce a:
$2\Delta rr+\Delta r^2=v^2\Delta t^2$
Como la variación del radio $\Delta r$ es mucho más pequeña que el radio en sí ($r\ll\Delta r$), podemos concluir que:
$2\Delta rr=v^2\Delta t^2$
o despejando $\Delta r$:
$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
Comparando esta ecuación con la ecuación $s=at^2/2$, se concluye que el cuerpo acelera con una aceleración igual a $v^2/r$.
ID:(313, 0)
Aceleración centrifuga
Ecuación
Los cuerpos tienden, por inercia, a desplazarse en línea recta a velocidad constante. Por lo tanto, si un cuerpo orbita alrededor de otro, se desviará de su trayectoria rectilínea y 'caerá' en una órbita. De manera similar, si no hay algo que retenga a un cuerpo, comenzará a alejarse de la órbita experimentando, para un objeto en el centro del sistema que rota, una aparente aceleración que lo aleja del centro, lo cual se conoce como aceleración centrífuga. La aceleración se define como:
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
Si la distancia recorrida es pequeña ($v\Delta t\ll r$), la raíz cuadrada de la distancia entre el centro y el cuerpo,
$\sqrt{r^2+(v\Delta t)^2}$
puede aproximarse como
$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
lo cual corresponde a una parábola en función del tiempo $\Delta t$. Por lo tanto, el comportamiento puede describirse con una aceleración igual a:
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
La aceleración centrífuga es una aceleración que un sistema observa en el eje de rotación cuando un objeto se aleja (fuga) a velocidad constante. Para el objeto que se aleja, no existe dicha aceleración.
ID:(4735, 0)
Aceleración centripeta
Ecuación
Cuando un objeto orbita en un radio $r$ y tiene una velocidad tangencial $v$, mantiene de forma permanente una distancia al centro igual al radio.
Para un observador externo al sistema, el cuerpo, que por inercia viajaría en línea recta, se desvía de esta trayectoria manteniendo la distancia al centro. Desde el punto de vista de este observador, el cuerpo está acelerando hacia el centro (centrípeta) de la órbita. A diferencia de la aceleración centrífuga, el objeto está experimentando una aceleración real. La magnitud de esta aceleración es igual a la aceleración centrífuga, pero con el signo opuesto. Por lo tanto, la magnitud de la aceleración centrípeta es:
| $ a_p =\displaystyle\frac{ v ^2}{ r }$ |
A diferencia de la aceleración centrífuga, la aceleración centrípeta es mensurable para el objeto que literalmente 'cae' hacia el centro.
ID:(4383, 0)
Momento de inercia de una partícula
Ecuación
Para una partícula de masa $m$ que orbita alrededor de un eje a una distancia equivalente a un radio $r$, se puede determinar la relación al comparar el momento angular expresado en términos del momento de inercia y del momento, que es igual a:
| $ I = m r ^2$ |
La relación entre momento angular y momento es igual a
| $ L = r p $ |
se puede igualar a
| $ L = I \omega $ |
que tras remplazar
| $ p = m_i v $ |
y
| $ v = r \omega $ |
se puede concluir que la momento de inercia de una partícula girando en una órbita es
| $ I = m r ^2$ |
.
ID:(3602, 0)