Fuerza e Impulsarse
Storyboard 
En la parte de la dinámica vimos que tanto la traslación como la rotación de nuestros miembros se puede analizar en función de la aceleración y la aceleración angular.
Para lograr dichas aceleraciones nuestros músculos deben generar fuerzas $F$ que vía las articulaciones de radios $r$ generan el torque
$T = Fr$
que mediante el momento de inercia de nuestros miembros $I$ genera la aceleración angular
$\alpha = \displaystyle\frac{T}{I}$
necesario para mover nuestros miembros. Dicho movimiento finalmente es el que nos permite desplazarnos a velocidades
$v=l\omega$
que dependen del largo de nuestras piernas $l$ y la velocidad angular de nuestros miembros.
ID:(319, 0)
Fuerza e Impulsarse
Descripción 
En la parte de la dinámica vimos que tanto la traslación como la rotación de nuestros miembros se puede analizar en función de la aceleración y la aceleración angular. Para lograr dichas aceleraciones nuestros músculos deben generar fuerzas $F$ que vía las articulaciones de radios $r$ generan el torque $T = Fr$ que mediante el momento de inercia de nuestros miembros $I$ genera la aceleración angular $\alpha = \displaystyle\frac{T}{I}$ necesario para mover nuestros miembros. Dicho movimiento finalmente es el que nos permite desplazarnos a velocidades $v=l\omega$ que dependen del largo de nuestras piernas $l$ y la velocidad angular de nuestros miembros.
Variables
Cálculos
Cálculos
Ecuaciones
La momento (vector) ($\vec{p}$) puede expresarse como un conjunto de sus diferentes componentes:
$\vec{p}=(p_x,p_y,p_z)$
Su derivada puede ser expresada como la derivada de cada una de sus componentes, entonces con:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
obtenemos, al derivar con respecto a el tiempo ($t$), que
$\displaystyle\frac{d}{dt}\vec{p}=\displaystyle\frac{d}{dt}(p_x,p_y,p_z)=\left(\displaystyle\frac{dp_x}{dt},\displaystyle\frac{dp_y}{dt},\displaystyle\frac{dp_z}{dt}\right)=(F_x,F_y,F_z)=\vec{F}$
lo que permite determinar la fuerza ($\vec{F}$):
| $\vec{F}=\displaystyle\frac{d\vec{p}}{dt}$ |
(ID 3239)
Dado que la relaci n con la fuerza de acción ($F_A$) y la fuerza de reacción ($F_R$) en una dimensi n es
| $ F_R =- F_A $ |
se puede aplicar a cada componente de la fuerza de acción (vector) ($\vec{F}_A$) y la fuerza de reacción (vector) ($\vec{F}_R$), lo que resulta en
$\vec{F}R=(F{Rx},F_{Ry},F_{Rz})=(-F_{Ax},-F_{Ay},-F_{Az})=-\vec{F}_A$
Por lo tanto,
| $ \vec{F}_R = - \vec{F}_A $ |
(ID 3240)
Dado que la magnitud del torque es
| $ T = r F $ |
Si el vector del eje es
$\hat{n}=\hat{r}\times\hat{t}$
Por lo tanto, dado que
$\vec{F} =F\hat{t}$
,
$\vec{r} =r\hat{r}$
,
$\vec{T}=T\hat{n}$
tenemos que
$\vec{T} =T\hat{n}=T\hat{r}\times\hat{t}=rF\hat{r}\times\hat{t}=\vec{r}\times\vec{F}$
lo que significa que
| $ \vec{T} = \vec{r} \times \vec{F} $ |
(ID 3249)
En el caso de una balanza, act a una fuerza gravitacional sobre cada brazo que genera un torque
| $ T = r F $ |
Si la longitud de los brazos es $d_i$ y las fuerzas son $F_i$ con $i=1,2$, la condici n de equilibrio exige que la suma de los torques sea cero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Por lo tanto, considerando que el signo de cada torque depende de la direcci n en la que est induciendo el giro,
$d_1F_1-d_2F_2=0$
de lo que resulta
| $ d_1 F_1 = d_2 F_2 $ |
.
(ID 3250)
(ID 3251)
Con la definici n de torque medio:
| $ T_m =\displaystyle\frac{ \Delta L }{ \Delta t }$ |
\\n\\nse puede pasar al limite instant neo en la medida que se consideren tiempos infinitesimales
$T\equiv \lim_{t\rightarrow 0}\displaystyle\frac{\Delta L}{\Delta t}\equiv \displaystyle\frac{dL}{dt}$
con lo que el torque instantaneo se define con la derivada del momento angular:
| $ T =\displaystyle\frac{d L }{d t }$ |
(ID 3252)
Dado que el momento es igual a
| $ L = I \omega $ |
se sigue que en el caso en que el momento de inercia no cambia con el tiempo,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
lo que implica que
| $ T = I \alpha $ |
.
(ID 3253)
La velocidad (vector) ($\vec{v}$) pode ser expresada como un conjunto de diferentes componentes:
$\vec{v}=(v_x,v_y,v_z)$
La derivada pode ser expressa como a derivada de cada una de sus componentes, osea con la masa inercial ($m_i$):
$m_i\displaystyle\frac{d}{dt}\vec{v}=m_i\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=m_i (a_x,a_y,a_z)=m_i\vec{a}$
Dado que la fuerza ($F$)
| $ F = m_i a $ |
obtemos, que la fuerza ($\vec{F}$) es:
| $ \vec{F} = m_i \vec{a} $ |
(ID 3598)
Si el momento ($p$) se define con la masa inercial ($m_i$) y la velocidad ($v$) como
| $ p = m_i v $ |
Esta relaci n puede generalizarse para m s de una dimensi n. En ese sentido, si definimos el vector de la velocidad de las partículas (vector) ($\vec{v}$) y la momento (vector) ($\vec{p}$) como
$\vec{p}=(p_x,p_y,p_z)=(m_iv_x,m_iv_y,m_iv_z)=m_i(v_x,v_y,v_z)=m_i\vec{v}$
entonces
| $ \vec{p} = m_i \vec{v} $ |
(ID 3599)
(ID 3683)
Si consideramos la variaci n del momento en el tiempo $t+\Delta t$ y en $t$ como:
$\Delta p = p(t+\Delta t)-p(t)$
y $\Delta t$ como el tiempo transcurrido, entonces en el l mite de tiempos infinitesimalmente peque os:
$F_m=\displaystyle\frac{\Delta p}{\Delta t}=\displaystyle\frac{p(t+\Delta t)-p(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{p(t+\Delta t)-p(t)}{\Delta t}=\displaystyle\frac{dp}{dt}$
Esta ltima expresi n corresponde a la derivada de la funci n de posici n $p(t)$:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
que a su vez es la pendiente de la representaci n gr fica de dicha funci n en el tiempo.
(ID 3685)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Ejemplos
El momento ($p$) es una medida de la cantidad de movimiento que aumenta tanto con la masa inercial ($m_i$) como con la velocidad ($v$).
| $ p = m_i v $ |
En casos de mayor n mero de dimensiones, la velocidad se convierte en un vector la velocidad (vector) ($\vec{v}$) y, por lo tanto, tambi n lo hace la momento (vector) ($\vec{p}$):
| $ \vec{p} = m_i \vec{v} $ |
(ID 3599)
Seg n Galileo, los cuerpos tienden a mantener su estado de movimiento, lo que hoy denominamos la variación del momento ($\Delta p$) y que se calcula con la masa inercial ($m_i$) y la velocidad ($v$) mediante
| $ p = m_i v $ |
debe ser constante. Si hay alguna acci n sobre el sistema que afecte su movimiento, estar asociada a la variación del momento ($\Delta p$) que se calcula de el momento ($p$) y el momento inicial ($p_0$) con:
| $ dp = p - p_0 $ |
(ID 3683)
Si no act a una fuerza sobre un cuerpo, el momento de inercia permanecer constante. Esto significa que el producto de la masa inercial ($m_i$) y la velocidad ($v$) se mantendr constante. Es decir, si la masa aumenta, la velocidad se reducir , y viceversa. Para entender por qu ocurre esto, podemos imaginar un carro con una cierta masa y velocidad al que se le a ade una masa adicional que, en nuestro sistema, est en reposo y, por lo tanto, no tiene momento. El carro deber transferir parte de su momento a la nueva masa para que esta adquiera la misma velocidad que el carro, lo que resultar en una disminuci n del momento y, por lo tanto, de la velocidad del carro:
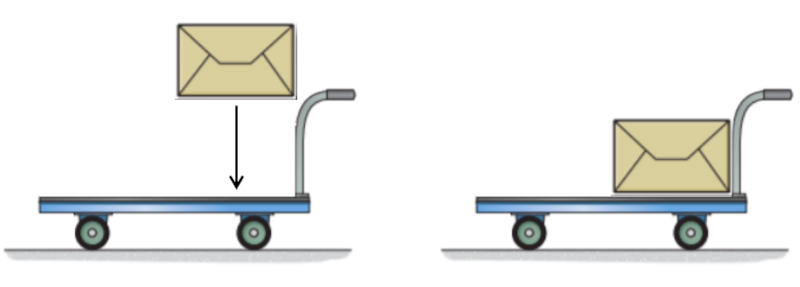
Por otro lado, si arrojamos una masa desde un carro en movimiento de manera que esta se detenga por completo, habremos recuperado el momento que la masa pose a, incrementando as el momento del carro y, con ello, su velocidad. Esto solo es posible si la masa se detiene al ser arrojada; si simplemente la dejamos "libre", continuar movi ndose a la misma velocidad.
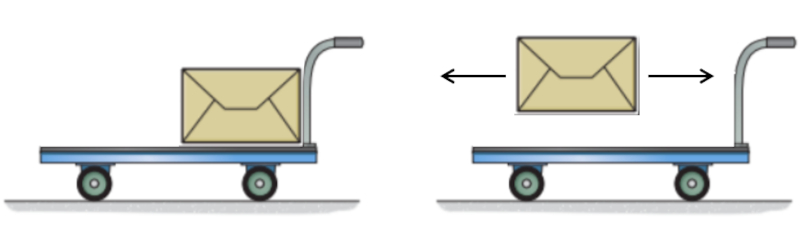
Este ltimo proceso tambi n nos ayuda a entender el tercer principio de la acci n y reacci n, ya que al actuar sobre la masa que liberamos, estamos obteniendo la reacci n correspondiente.
(ID 3238)
En general, la fuerza con masa constante ($F$) debe ser entendida como un vector tridimensional, es decir, la fuerza ($\vec{F}$). Esto significa que el momento ($p$) se describe mediante un vector la momento (vector) ($\vec{p}$). De esta forma la expresi n con el tiempo ($t$):
| $ F =\displaystyle\frac{ dp }{ dt }$ |
se generaliza como:
| $\vec{F}=\displaystyle\frac{d\vec{p}}{dt}$ |
Es importante tener en cuenta que la fuerza act a en la direcci n y sentido de la variaci n del vector impulso en el tiempo.
(ID 3239)
La fuerza ($F$) se define como la variación del momento ($\Delta p$) por el tiempo transcurrido ($\Delta t$) que se define con la relaci n:
| $ F \equiv\displaystyle\frac{ \Delta p }{ \Delta t }$ |
(ID 3684)
La fuerza ($F$) se calcula como la variación del momento ($\Delta p$) dividido por el tiempo transcurrido ($\Delta t$), seg n la siguiente f rmula:
| $ F \equiv\displaystyle\frac{ \Delta p }{ \Delta t }$ |
Esta f rmula es una aproximaci n de la fuerza real y puede distorsionarse si la fuerza fluct a durante el intervalo de tiempo. Por esta raz n, se introduce el concepto de la fuerza con masa constante ($F$) determinada en un intervalo de tiempo infinitesimalmente peque o lo que corresponde a la derivada de el momento ($p$) en el tiempo ($t$) que se expresa como:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
(ID 3685)
Para el caso en que la masa inercial ($m_i$) sea constante, tambi n se aplica que la fuerza con masa constante ($F$) debe entenderse como un vector tridimensional, es decir, la fuerza ($\vec{F}$). Esto implica que la aceleración instantanea ($a$) se describe mediante un vector la aceleración instantánea (vector) ($\vec{a}$). De esta manera, la expresi n con la fuerza con masa constante ($F$):
| $ F = m_i a $ |
se generaliza como:
| $ \vec{F} = m_i \vec{a} $ |
(ID 3598)
La relaci n entre la fuerza de acción ($F_A$) y la fuerza de reacción ($F_R$) unidimensional
| $ F_R =- F_A $ |
se puede generalizar para m s dimensiones con la fuerza de acción (vector) ($\vec{F}_A$) y la fuerza de reacción (vector) ($\vec{F}_R$) como
| $ \vec{F}_R = - \vec{F}_A $ |
(ID 3240)
El momento ($p$) fue definido como el producto de la masa inercial ($m_i$) y la velocidad ($v$), lo cual es igual a:
| $ p = m_i v $ |
El an logo de la velocidad ($v$) en el caso de la rotaci n es la velocidad angular instantánea ($\omega$), por lo tanto, el equivalente a el momento ($p$) deber a ser un el momento Angular ($L$) de la forma:
| $ L = I \omega $ |
.
la masa inercial ($m_i$) se asocia con la inercia en la traslaci n de un cuerpo, por lo que el momento de inercia ($I$) corresponde a la inercia en la rotaci n de un cuerpo.
(ID 3251)
Si el momento angular se mantiene constante
| $L=L_0$ |
se tiene con
| $ L = I \omega $ |
se tiene que variaciones en el momento de inercia es compensado con variaciones en la velocidad angular
| $ I_1 \omega_1 = I_2 \omega_2 $ |
(ID 3600)
El torque medio calculado con la variaci n del momento angular
| $ T_m =\displaystyle\frac{ \Delta L }{ \Delta t }$ |
por ello el torque instantaneo se puede definir en el limite de tiempo infinitesimal:
| $ T =\displaystyle\frac{d L }{d t }$ |
(ID 3252)
En el escenario en el que el momento de inercia es constante, la derivada del momento angular es igual a
| $ L = I \omega $ |
lo cual implica que el torque es igual a
| $ T = I \alpha $ |
Esta relaci n equivale a la segunda ley de Newton en el contexto de la rotaci n en lugar de la traslaci n.
(ID 3253)
Tanto la primera como la segunda ley de Newton son aplicables a la rotaci n.
La inercia explica que los objetos tienden a mantener una velocidad angular constante al rotar.
La variaci n del momento angular en el tiempo se relaciona con el torque, que, de manera an loga a la fuerza en la traslaci n, es lo que causa la rotaci n.
En cuanto al tercer principio, que establece que a toda acci n le corresponde una reacci n igual y opuesta:
| $ \vec{F}_R = - \vec{F}_A $ |
en forma similar, para cada torque aplicado $T_a$ existe un torque de reacci n $T_r$ de igual magnitud pero direcci n opuesta:
| $ \vec{T}_R =- \vec{T}_A $ |
Esto significa en t rminos f sicos que siempre necesitamos un punto de apoyo para generar torque, de modo que el sistema pueda experimentar el torque de reacci n.
(ID 3254)
Dado que la relaci n entre el momento angular y el momento es
| $ L = r p $ |
su derivada temporal nos conduce a la relaci n de torque
| $ T = r F $ |
La rotaci n del cuerpo tiene lugar alrededor de un eje en la direcci n del torque, que atraviesa el centro de masa.
(ID 4431)
El torque se representa como un vector en la direcci n del eje de rotaci n. Dado que el radio de rotaci n y la fuerza son perpendiculares entre s , la relaci n es
| $ T = r F $ |
y esto puede expresarse como el producto cruz entre la velocidad angular y el radio:
| $ \vec{T} = \vec{r} \times \vec{F} $ |
(ID 3249)
Si una barra montada sobre un punto que act a como eje es sometida a la fuerza 1 ($F_1$) a el distancia fuerza - eje (brazo) 1 ($d_1$) del eje, generando un torque $T_1$, y a la fuerza 2 ($F_2$) a el distancia fuerza - eje (brazo) 2 ($d_2$) del eje, generando un torque $T_2$, estar en equilibrio cuando ambos torques sean iguales. Por lo tanto, el equilibrio se describe mediante la llamada ley de la palanca, expresada como:
| $ d_1 F_1 = d_2 F_2 $ |
(ID 3250)
ID:(319, 0)
