Benützer:
Impulsarse y Caminar
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Die Momento (vector) ($\vec{p}$) kann als eine Reihe seiner verschiedenen Komponenten ausgedr ckt werden:
$\vec{p}=(p_x,p_y,p_z)$
Seine Ableitung kann als die Ableitung jeder seiner Komponenten ausgedr ckt werden, daher mit:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
erhalten wir, indem wir nach der Zeit ($t$) differenzieren, dass
$\displaystyle\frac{d}{dt}\vec{p}=\displaystyle\frac{d}{dt}(p_x,p_y,p_z)=\left(\displaystyle\frac{dp_x}{dt},\displaystyle\frac{dp_y}{dt},\displaystyle\frac{dp_z}{dt}\right)=(F_x,F_y,F_z)=\vec{F}$
was es uns erm glicht, die Kraft ($\vec{F}$) zu bestimmen:
| $\vec{F}=\displaystyle\frac{d\vec{p}}{dt}$ |
(ID 3239)
Da die Beziehung zu die Aktion Kraft ($F_A$) und die Reaktion Kraft ($F_R$) in einer Dimension lautet
| $ F_R =- F_A $ |
kann sie auf jede Komponente von die Aktion Kraft (Vektor) ($\vec{F}_A$) und die Reaktion Kraft (Vektor) ($\vec{F}_R$) angewendet werden, was zu
$\vec{F}R=(F{Rx},F_{Ry},F_{Rz})=(-F_{Ax},-F_{Ay},-F_{Az})=-\vec{F}_A$
f hrt. Daher gilt
| $ \vec{F}_R = - \vec{F}_A $ |
(ID 3240)
Da die Gr e des Drehmoments ist
| $ T = r F $ |
Wenn der Achseneinheitsvektor
$\hat{n}=\hat{r}\times\hat{t}$
Daher, unter Ber cksichtigung von
$\vec{F} =F\hat{t}$
,
$\vec{r} =r\hat{r}$
,
$\vec{T}=T\hat{n}$
haben wir
$\vec{T} =T\hat{n}=T\hat{r}\times\hat{t}=rF\hat{r}\times\hat{t}=\vec{r}\times\vec{F}$
was bedeutet
| $ \vec{T} = \vec{r} \times \vec{F} $ |
(ID 3249)
Im Falle einer Waage wirkt auf jeden Arm eine Gravitationskraft, die ein Drehmoment erzeugt
| $ T = r F $ |
Wenn die L ngen der Arme $d_i$ betragen und die Kr fte $F_i$ mit $i=1,2$ sind, verlangt die Gleichgewichtsbedingung, dass die Summe der Drehmomente null ist:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Daher, unter Ber cksichtigung, dass das Vorzeichen jedes Drehmoments von der Richtung abh ngt, in der es eine Rotation induziert,
$d_1F_1-d_2F_2=0$
was zu
| $ d_1 F_1 = d_2 F_2 $ |
f hrt.
(ID 3250)
(ID 3251)
Con la definici n de torque medio:
| $ T_m =\displaystyle\frac{ \Delta L }{ \Delta t }$ |
\\n\\nse puede pasar al limite instant neo en la medida que se consideren tiempos infinitesimales
$T\equiv \lim_{t\rightarrow 0}\displaystyle\frac{\Delta L}{\Delta t}\equiv \displaystyle\frac{dL}{dt}$
con lo que el torque instantaneo se define con la derivada del momento angular:
| $ T =\displaystyle\frac{d L }{d t }$ |
(ID 3252)
Da das Moment gleich ist
| $ L = I \omega $ |
folgt daraus, dass im Fall, dass sich das Tr gheitsmoment nicht mit der Zeit ndert,
$T=\displaystyle\frac{dL}{dt}=\displaystyle\frac{d}{dt}(I\omega) = I\displaystyle\frac{d\omega}{dt} = I\alpha$
was bedeutet, dass
| $ T = I \alpha $ |
.
(ID 3253)
Da ein Vektor als Array seiner verschiedenen Komponenten ausgedr ckt werden kann
$\vec{a}=(a_x,a_y,a_z)$
kann seine Ableitung als Ableitung jeder seiner Komponenten ausgedr ckt werden
$m_i\displaystyle\frac{d}{dt}\vec{a}=m_i\displaystyle\frac{d}{dt}(a_x,a_y,a_z)=\left(m_i\displaystyle\frac{da_x}{dt},m_i\displaystyle\frac{da_y}{dt},m_i\displaystyle\frac{da_z}{dt}\right)=(F_x,F_y,F_z)=\vec{F}$
Daher ist im Allgemeinen die momentane Geschwindigkeit in mehreren Dimensionen
| $ \vec{F} = m_i \vec{a} $ |
(ID 3598)
Wenn der Moment ($p$) definiert ist mit die Träge Masse ($m_i$) und die Geschwindigkeit ($v$) als
| $ p = m_i v $ |
Diese Beziehung kann f r mehr als eine Dimension verallgemeinert werden. In diesem Sinne, wenn wir den Vektor von die Velocidad de las partículas (vector) ($\vec{v}$) und die Momento (vector) ($\vec{p}$) definieren als
$\vec{p}=(p_x,p_y,p_z)=(m_iv_x,m_iv_y,m_iv_z)=m_i(v_x,v_y,v_z)=m_i\vec{v}$
dann
| $ \vec{p} = m_i \vec{v} $ |
(ID 3599)
(ID 3683)
Wenn wir die nderung des Impulses ber die Zeit $t+\Delta t$ und bei $t$ betrachten:
$\Delta p = p(t+\Delta t)-p(t)$
und $\Delta t$ die verstrichene Zeit ist, dann ergibt sich im Grenzwert unendlich kleiner Zeitintervalle:
$F_m=\displaystyle\frac{\Delta p}{\Delta t}=\displaystyle\frac{p(t+\Delta t)-p(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{p(t+\Delta t)-p(t)}{\Delta t}=\displaystyle\frac{dp}{dt}$
Dieser letzte Ausdruck entspricht der Ableitung der Positionsxadfunktion $p(t)$:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
die auch die Steigung des Graphen darstellt, der diese Funktion ber der Zeit darstellt.
(ID 3685)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Beispiele
Der Impuls ist eine Ma zahl f r die Bewegungsmenge, die sowohl mit der Masse als auch mit der Geschwindigkeit zunimmt.
In F llen mit mehr Dimensionen wird die Geschwindigkeit zu einem Vektor und somit auch der Impuls:
| $ \vec{p} = m_i \vec{v} $ |
(ID 3599)
Nach Galileo tendieren K rper dazu, ihren Bewegungszustand beizubehalten, das bedeutet, der Impuls
$\vec{p} = m\vec{v}$
sollte konstant bleiben. Wenn es eine Einwirkung auf das System gibt, die seine Bewegung beeinflusst, wird dies mit einer Ver nderung des Impulses verbunden sein. Die Differenz zwischen dem anf nglichen Impuls $\vec{p}_0$ und dem endg ltigen Impuls $\vec{p}$ kann wie folgt ausgedr ckt werden:
| $ dp = p - p_0 $ |
(ID 3683)
Wenn keine Kraft auf einen K rper wirkt, bleibt sein Tr gheitsmoment konstant. Das bedeutet, dass das Produkt aus die Träge Masse ($m_i$) und die Geschwindigkeit ($v$) konstant bleibt. Mit anderen Worten: Wenn die Masse zunimmt, wird die Geschwindigkeit abnehmen, und umgekehrt. Um zu verstehen, warum dies geschieht, stellen wir uns einen Wagen mit einer bestimmten Masse und Geschwindigkeit vor, dem eine zus tzliche Masse hinzugef gt wird. Diese zus tzliche Masse befindet sich in unserem System zun chst in Ruhe und hat daher keinen Impuls. Der Wagen muss einen Teil seines Impulses auf die neue Masse bertragen, damit diese die gleiche Geschwindigkeit wie der Wagen erreicht, was zu einem Verlust an Impuls und damit zu einer Verringerung der Geschwindigkeit des Wagens f hrt:
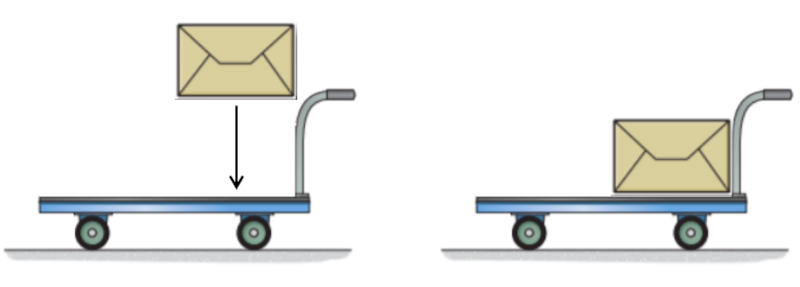
Umgekehrt, wenn wir eine Masse von einem sich bewegenden Wagen so abwerfen, dass die Masse vollst ndig zum Stillstand kommt, gewinnen wir den Impuls zur ck, den die Masse hatte, wodurch sich der Impuls des Wagens erh ht und damit auch seine Geschwindigkeit. Dies kann nur geschehen, wenn die Masse beim Abwerfen zum Stillstand kommt; wenn sie einfach freigegeben wird, bewegt sie sich mit der gleichen Geschwindigkeit weiter.
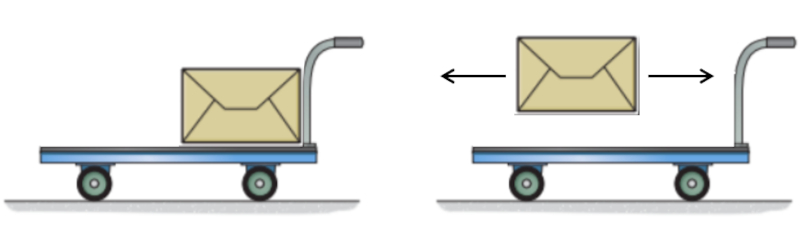
Dieser letzte Prozess hilft uns auch, das dritte Newtonsche Gesetz von Aktion und Reaktion zu verstehen, da wir durch das Einwirken auf die freigesetzte Masse die entsprechende Reaktion ernten.
(ID 3238)
Im Allgemeinen sollte die Kraft mit konstanter Masse ($F$) als ein dreidimensionaler Vektor verstanden werden, das hei t, die Kraft ($\vec{F}$). Das bedeutet, dass der Moment ($p$) durch einen Vektor die Momento (vector) ($\vec{p}$) beschrieben wird. Somit wird der Ausdruck mit der Zeit ($t$):
| $ F =\displaystyle\frac{ dp }{ dt }$ |
verallgemeinert als:
| $\vec{F}=\displaystyle\frac{d\vec{p}}{dt}$ |
Es ist wichtig zu beachten, dass die Kraft in Richtung und Sinn der nderung des Impulsvektors im Laufe der Zeit wirkt.
(ID 3239)
Die Kraft ($F$) wird als die Impulsvariation ($\Delta p$) durch der Abgelaufene Zeit ($\Delta t$) definiert, das durch die Beziehung definiert ist:
| $ F \equiv\displaystyle\frac{ \Delta p }{ \Delta t }$ |
(ID 3684)
Die mittlere Kraft wird als nderung des Impulses $\Delta p$ durch die verstrichene Zeit $\Delta t$ berechnet, mit der Formel:
| $ F \equiv\displaystyle\frac{ \Delta p }{ \Delta t }$ |
Dies ist eine N herung an die tats chliche Kraft, die sich verzerren kann, wenn die Kraft w hrend des Zeitintervalls schwankt. Daher wird das Konzept einer instantanen Kraft eingef hrt, die ber einen infinitesimal kleinen Zeitraum bestimmt wird.
| $ F =\displaystyle\frac{ dp }{ dt }$ |
entspricht der Ableitung des Impulses und repr sentiert die momentane Kraft.
(ID 3685)
Auch f r den Fall, dass die Träge Masse ($m_i$) konstant ist, gilt, dass die Kraft mit konstanter Masse ($F$) als dreidimensionaler Vektor verstanden werden sollte, das hei t, die Kraft ($\vec{F}$). Dies bedeutet, dass die Augenblickliche Beschleunigung ($a$) durch einen Vektor die Momentane Beschleunigung (Vektor) ($\vec{a}$) beschrieben wird. Somit wird der Ausdruck mit die Kraft mit konstanter Masse ($F$):
| $ F = m_i a $ |
verallgemeinert als:
| $ \vec{F} = m_i \vec{a} $ |
(ID 3598)
Die Beziehung zwischen die Aktion Kraft ($F_A$) und die Reaktion Kraft ($F_R$) in einer Dimension:
| $ F_R =- F_A $ |
kann auf mehrere Dimensionen mit die Aktion Kraft (Vektor) ($\vec{F}_A$) und die Reaktion Kraft (Vektor) ($\vec{F}_R$) verallgemeinert werden, wie folgt:
| $ \vec{F}_R = - \vec{F}_A $ |
(ID 3240)
Der Moment ($p$) wurde als das Produkt von die Träge Masse ($m_i$) und die Geschwindigkeit ($v$) definiert, was gleich ist zu:
| $ p = m_i v $ |
Das Analogon zu die Geschwindigkeit ($v$) im Fall der Rotation ist die Augenblickliche Winkelgeschwindigkeit ($\omega$), daher sollte das quivalent zu der Moment ($p$) ein der Angular Momentum ($L$) in der Form sein:
| $ L = I \omega $ |
.
die Träge Masse ($m_i$) ist mit der Tr gheit bei der Translation eines K rpers verbunden, daher entspricht der Massenträgheitsmoment ($I$) der Tr gheit bei der Rotation eines K rpers.
(ID 3251)
Si el momento angular se mantiene constante
| $L=L_0$ |
se tiene con
| $ L = I \omega $ |
se tiene que variaciones en el momento de inercia es compensado con variaciones en la velocidad angular
| $ I_1 \omega_1 = I_2 \omega_2 $ |
(ID 3600)
El torque medio calculado con la variaci n del momento angular
| $ T_m =\displaystyle\frac{ \Delta L }{ \Delta t }$ |
por ello el torque instantaneo se puede definir en el limite de tiempo infinitesimal:
| $ T =\displaystyle\frac{d L }{d t }$ |
(ID 3252)
Im Fall, dass das Tr gheitsmoment konstant ist, ist die Ableitung des Drehimpulses gleich
| $ L = I \omega $ |
was bedeutet, dass das Drehmoment gleich ist
| $ T = I \alpha $ |
Diese Beziehung entspricht dem quivalent des zweiten Newtonschen Gesetzes f r Rotation anstelle von Translation.
(ID 3253)
Sowohl das erste als auch das zweite Newtonsche Gesetz gelten f r die Rotation.
Die Tr gheit erkl rt, dass Objekte dazu tendieren, eine konstante Winkelgeschwindigkeit beizubehalten, w hrend sie sich drehen.
Ver nderungen im Drehimpuls im Laufe der Zeit stehen im Zusammenhang mit dem Drehmoment, das analog zur Kraft bei der Translation ist und die Rotation verursacht.
Im Fall des dritten Prinzips, das jede Aktion mit einer gleich gro en und entgegengesetzten Reaktion verkn pft:
| $ \vec{F}_R = - \vec{F}_A $ |
auf hnliche Weise gibt es f r jedes angewandte Drehmoment $T_a$ ein Reaktionsdrehmoment $T_r$ gleicher Gr e, aber entgegengesetzter Richtung:
| $ \vec{T}_R =- \vec{T}_A $ |
Dies bedeutet physisch, dass wir immer einen Drehpunkt ben tigen, um ein Drehmoment zu erzeugen, damit das System das Reaktionsdrehmoment erf hrt.
(ID 3254)
Da das Verh ltnis zwischen dem Drehimpuls und dem Moment wie folgt ist:
| $ L = r p $ |
f hrt uns die zeitliche Ableitung zu der Beziehung des Drehmoments
| $ T = r F $ |
Die Drehung des K rpers erfolgt um eine Achse in Richtung des Drehmoments, das durch den Schwerpunkt verl uft.
(ID 4431)
Das Drehmoment wird als Vektor in Richtung der Rotationsachse dargestellt. Da der Rotationsradius und die Kraft senkrecht zueinander stehen, ergibt sich die Beziehung
| $ T = r F $ |
Dies kann als Kreuzprodukt aus Winkelgeschwindigkeit und Radius ausgedr ckt werden:
| $ \vec{T} = \vec{r} \times \vec{F} $ |
(ID 3249)
Wenn eine Stange, die auf einem Punkt als Drehachse montiert ist, an die Kraft 1 ($F_1$) bei der Abstand Kraft - Achse (Arm) 1 ($d_1$) von der Achse ein Drehmoment $T_1$ erzeugt und an die Kraft 2 ($F_2$) bei der Abstand Kraft - Achse (Arm) 2 ($d_2$) ein Drehmoment $T_2$, dann ist sie im Gleichgewicht, wenn beide Drehmomente gleich sind. Das Gleichgewicht entspricht somit dem sogenannten Hebelgesetz, ausgedr ckt als:
| $ d_1 F_1 = d_2 F_2 $ |
(ID 3250)
ID:(319, 0)