Estructura del hueso
Script 
La estructura microscópica del hueso se puede describir como un sistema de numerosos puentes. Al sufrir la persona ortoporosis son estos puentes los que se reducen lo que cambia tanto las propiedades de deformación como la tensión critica que pueden soportar.
ID:(738, 0)
Deformación de Huesos
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Como la la constante de Hook total de resortes en paralelo ($k_p$) de la constante de Hook de resorte i ($k_i$) es
| $ k_p =\displaystyle\sum_i k_i$ |
se tiene que para el caso de la constante de Hook microscópica ($k_m$) iguales que
$k_p = N_p k_m$
la constante de Hook total de resortes en paralelo ($k_p$) corresponde, en este caso, a la constante de Hook de una secci n de un grosor monoat mico. Para obtener la constante de todo el cuerpo, se debe sumar ahora en serie todas las secciones, para lo que se trabaja con la relaci n para la suma de la constante de Hook total de resortes en serie ($k_s$), dada por
| $\displaystyle\frac{1}{ k_s }=\displaystyle\sum_i\displaystyle\frac{1}{ k_i }$ |
Con el n mero de secciones igual a el número de resortes en serie ($N_s$), y si se asume que todas son iguales, se obtiene
$\displaystyle\frac{1}{k} = N_s\displaystyle\frac{1}{N_p k_m}$
o sea
$k = \displaystyle\frac{N_p}{N_s}k_m$
Finalmente, con las relaciones para el largo del cuerpo ($L$) y el largo del resorte microscópico ($l$)
| $ N_s =\displaystyle\frac{ L }{ l }$ |
y con la sección del elemento ($S$) y la sección del resorte microscópico ($s$)
| $ N_p =\displaystyle\frac{ S }{ s }$ |
se obtiene finalmente
| $ k =\displaystyle\frac{ S }{ L }\displaystyle\frac{ l }{ s } k_m $ |
(ID 3205)
(ID 3207)
Cuando aplicamos fuerzas la fuerza ($F$) en los extremos de los resortes, los resortes se elongar n (o comprimir n) en la elongación del resorte i ($u_i$) y la constante de Hook de resorte i ($k_i$) respectivamente. Si el punto de contacto entre ambos resortes est en reposo, la suma de las fuerzas que act an sobre l debe ser igual a cero, es decir, deben ser iguales a la fuerza ($F$). Por lo tanto, en cada resorte $i$ debe cumplirse que
$F = k_iu_i$
La elongaci n total ser igual a la suma de las elongaciones individuales:
$u = \displaystyle\sum_iu_i$
Y utilizando la ley de Hooke, esto se expresa como:
$u = \displaystyle\sum_i\frac{F}{k_i}$
Si introducimos una constante total para el caso de conexi n en serie la constante de Hook total de resortes en serie ($k_s$), tal que
$F = k_su$
Entonces, se tiene:
| $\displaystyle\frac{1}{ k_s }=\displaystyle\sum_i\displaystyle\frac{1}{ k_i }$ |
(ID 3208)
Con la Ley de Hooke para la fuerza elástica ($F_k$), la constante de Hooke ($k$) y la elongación ($u$) de la siguiente forma:
| $ F_k = k u $ |
y la expresi n para la constante de Hooke ($k$) en funci n de el largo del cuerpo ($L$), la sección del elemento ($S$), el largo del resorte microscópico ($l$), la sección del resorte microscópico ($s$) y la constante de Hook microscópica ($k_m$):
| $ k =\displaystyle\frac{ S }{ L }\displaystyle\frac{ l }{ s } k_m $ |
combinada con la expresi n para el módulo de Elasticidad ($E$):
| $ E =\displaystyle\frac{ l }{ s } k_m $ |
el resultado es:
| $ F_k =\displaystyle\frac{ E S }{ L } u $ |
(ID 3209)
Dado que cada resorte est expuesto a la misma fuerza aplicada la fuerza ($F$), los resortes con constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) se deformar n en magnitudes la elongación del resorte 1 ($u_1$) y la elongación del resorte 2 ($u_2$) respectivamente, de acuerdo con las siguientes ecuaciones:
$F = k_1u_1$
$F = k_2u_2$
La elongaci n total ser la suma de ambas elongaciones:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Por lo tanto, el sistema se comporta como si tuviera una constante de resorte igual a:
| $\displaystyle\frac{1}{ k_s }=\displaystyle\frac{1}{ k_1 }+\displaystyle\frac{1}{ k_2 }$ |
(ID 3753)
Dado que cada resorte puede tener una constante de elasticidad distinta, representada por la constante de Hook de resorte i ($k_i$), la fuerza que cada resorte aporta tambi n var a. Seg n la ley de Hooke, las fuerzas $F_i$ se expresan como:
$F_i = k_i u$
Dado que la fuerza total $F$ es la suma de las fuerzas individuales, se obtiene:
$F =\displaystyle\sum_i F_i = \displaystyle\sum_i k_i u$
De esta manera, se puede definir una constante de elasticidad total:
| $ k_p =\displaystyle\sum_i k_i$ |
(ID 3756)
Dado que cada resorte est sujeto a la misma ERROR:5343,0, las fuerzas ser n diferentes si las constantes lo son. Por lo tanto, si la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) son las constantes, las fuerzas ser n las siguientes:
$F_1 = k_1 u$
$F_2 = k_2 u$
Como resultado, la fuerza total ser :
$F = F_1 + F_2 = k_1u + k_2u = (k_1 + k_2)u$
Por lo tanto, el sistema se comporta como si tuviera una constante de resorte igual a:
| $ k_p = k_1 + k_2 $ |
(ID 3757)
(ID 3759)
(ID 3771)
Ejemplos
Medici n de fuerzas: el dinam metro
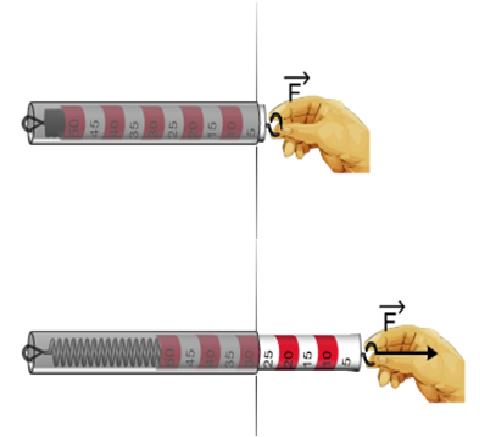
(ID 1909)
Medici n de la fuerza y elongaci n
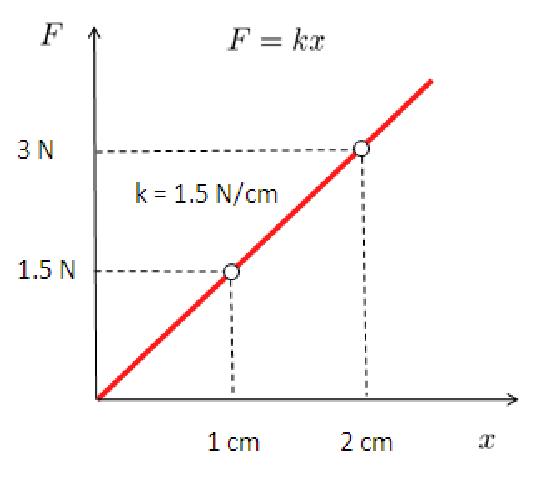
(ID 1908)
Resorte

(ID 1907)
Si se desea modelar c mo se deforma un s lido bajo la influencia de una fuerza, primero se puede considerar el comportamiento de una subunidad, como dos resortes conectados uno detr s del otro, como se muestra en la imagen:
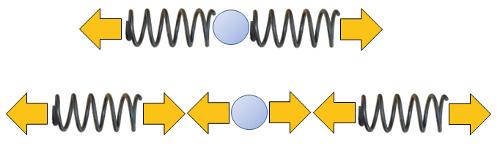
Este tipo de disposici n de los resortes se llama en serie. Se caracteriza porque la fuerza la fuerza ($F$) es igual en ambos resortes, y estos se deforman seg n la constante de Hooke ($k$). Por lo tanto, la constante el stica equivalente la elongación ($u$) se calcula como la suma de la elongación del resorte 1 ($u_1$) y la elongación del resorte 2 ($u_2$), que a su vez, seg n la ley de Hooke:
| $ F_k = k u $ |
es igual a la fuerza ($F$) dividido por las constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$), respectivamente:
$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$
Por lo tanto, el sistema de dos resortes se puede tratar como un solo resorte cuya constante el stica equivalente la constante de Hook total de resortes en serie ($k_s$) se calcula de la siguiente manera:
| $\displaystyle\frac{1}{ k_s }=\displaystyle\frac{1}{ k_1 }+\displaystyle\frac{1}{ k_2 }$ |
(ID 1910)
Si se desea modelar c mo se deforma un s lido bajo la influencia de una fuerza, primero se puede considerar el comportamiento de una subunidad, como dos resortes conectados uno al lado del otro, como se muestra en la imagen:

Este tipo de disposici n de los resortes se llama en paralelo. Se caracteriza porque la elongación ($u$) en ambos resortes es la misma y cada resorte aporta ERROR:4975,0 en funci n de la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) seg n la ley de Hooke:
| $ F_k = k u $ |
Por ello se tiene que:
$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$
Por lo tanto, el sistema de dos resortes se puede tratar como un solo resorte cuya constante el stica equivalente la constante de Hook total de resortes en paralelo ($k_p$) se calcula de la siguiente manera:
| $ k_p = k_1 + k_2 $ |
(ID 1692)
En el caso de dos resortes con constantes la constante de Hook de resorte 1 ($k_1$) y la constante de Hook de resorte 2 ($k_2$) que pueden ser modelados por un nico resorte con una constante la constante de Hook total de resortes en paralelo ($k_p$) calculada mediante la siguiente ecuaci n:
| $ k_p = k_1 + k_2 $ |
Para el caso m s general de resortes con constantes ERROR:10228,0, la ecuaci n puede generalizarse de la siguiente manera:
| $ k_p =\displaystyle\sum_i k_i$ |
Esto nos permite modelar una estructura macro de la siguiente manera:

(ID 1684)
La estructura microsc pica del hueso se puede describir como un sistema de numerosos puentes. Al sufrir la persona ortoporosis son estos puentes los que se reducen lo que cambia tanto las propiedades de deformaci n como la tensi n critica que pueden soportar.
(ID 738)
El hueso se puede modelar como un cilindro hueco, ya que el material en su interior no es capaz de soportar una carga significativa. Por lo tanto, se modela geom tricamente como un cilindro con propiedades el largo del cuerpo ($L$), el radio interior ($R_1$) y el radio exterior ($R_2$):

None
Por ello el radio efectivo ($R$) es
| $R^2=R_1^2+R_2^2$ |
la sección del elemento ($S$) es
| $ S = \pi ( R_2 ^2- R_1 ^2)$ |
y el momento de inercia de superficie ($I_s$) es
| $ I_s =\displaystyle\frac{ \pi }{2}( R_2 ^4- R_1 ^4)$ |
(ID 1915)
La deformaci n el stica microsc pica corresponde a una modificaci n de la distancia entre los tomos bajo una fuerza externa, sin que ocurra un reordenamiento de estos.
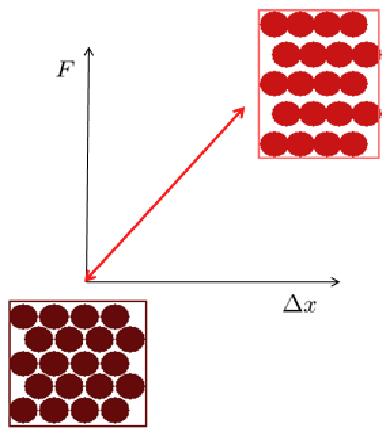
None
En general, es una deformaci n en la que la distancia se modifica de manera proporcional a la fuerza aplicada, y se habla de una deformaci n el stica.
(ID 1685)
La deformaci n pl stica implica que si se reduce la tensi n aplicada, el material disminuye su deformaci n pero termina con una deformaci n permanente.

None
Por lo tanto, si se somete nuevamente a tensi n, por lo general vuelve a su forma el stica, pero debido a la nueva forma, no puede recuperar su forma original.
(ID 1911)
Una situaci n que puede ocurrir es que una fuerza de deformación con dos puntos fijos ($F_2$) act e sobre un hueso con las propiedades un largo del cuerpo ($L$), el módulo de Elasticidad ($E$) y el momento de inercia de superficie ($I_s$), que est fijo en ambos extremos:

None
la energía de deformación con dos puntos fijos ($W_2$), que almacena la estructura frente a un desplazamiento en flexión con dos puntos fijos ($u_2$), es
| $ W_2 =\displaystyle\frac{24 E I_s }{ L ^3} u_2 ^2$ |
la fuerza de deformación con dos puntos fijos ($F_2$), que se aplica, lleva a un desplazamiento en flexión con dos puntos fijos ($u_2$), seg n
| $ F_2 =\displaystyle\frac{48 E I_s }{ L ^3} u_2 $ |
y la tensión para deformación con dos puntos fijos ($\sigma_2$), que depende de el radio exterior ($R_2$), es
| $ \sigma_2 =\displaystyle\frac{ R_2 L }{3 I_s } F_2 $ |
(ID 740)
Una situaci n que puede ocurrir es que una fuerza de deformación en condición de pandeo ($F_p$) act e a lo largo del eje del hueso con las propiedades un largo del cuerpo ($L$), el módulo de Elasticidad ($E$), el factor de pandeo ($K$), el radio efectivo ($R$) y el momento de inercia de superficie ($I_s$), generando pandeo:

None
la energía de deformación en condición de pandeo ($W_p$), se define como
| $ W_p =\displaystyle\frac{ \pi ^4 E I_s }{2 K ^4 L ^3} R ^2$ |
la fuerza de deformación en condición de pandeo ($F_p$), la fuerza aplicada, seg n
| $ F_p =\displaystyle\frac{ \pi ^2 E I_s }{ K ^2 L ^2}$ |
y la tensión para deformación en el caso de pandeo ($\sigma_p$), que depende de el radio exterior ($R_2$), se expresa como
| $ \sigma_p =\displaystyle\frac{ \pi ^2 E I_s }{ K ^2 L ^2 S }$ |
(ID 741)
Una deformaci n pl stica implica que los tomos se reordenen, disoci ndose de estructuras existentes y formando nuevas uniones que son estables en s mismas. Sin embargo, dicha deformaci n generalmente implica una modificaci n en la forma del medio.
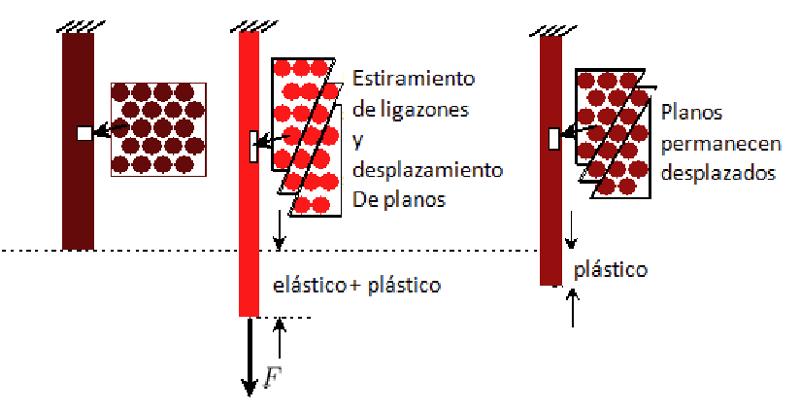
None
La deformaci n pl stica puede finalmente llevar a modificaciones que incluyen rupturas catastr ficas que son permanentes.
(ID 1686)
Una situaci n que puede ocurrir es que una fuerza de deformación con un punto fijo ($F_1$) act e sobre un hueso de un largo del cuerpo ($L$), el módulo de Elasticidad ($E$) y el momento de inercia de superficie ($I_s$) que est fijo en un extremo.
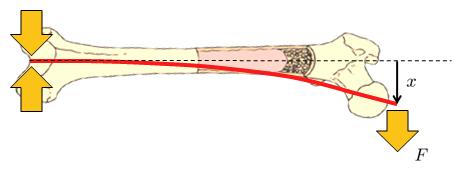
None
la energía de deformación con un punto fijo ($W_1$), que almacena la estructura ante una tensión para deformación con un punto fijo ($\sigma_1$), es
| $ W_1 =\displaystyle\frac{3 E I_s }{2 L ^3} u_1 ^2$ |
la fuerza de deformación con un punto fijo ($F_1$), que se aplica, lleva a una tensión para deformación con un punto fijo ($\sigma_1$), seg n
| $ F_1 =\displaystyle\frac{3 E I_s }{ L ^3} u_1 $ |
y la tensión para deformación con un punto fijo ($\sigma_1$), que depende de el radio exterior ($R_2$), es
| $ \sigma_1 =\displaystyle\frac{2 R_2 L }{3 I_s } F_1 $ |
(ID 739)
Una de las formas de generar una fractura es mediante la torsi n del hueso, que implica la aplicaci n de torques opuestos en los extremos:
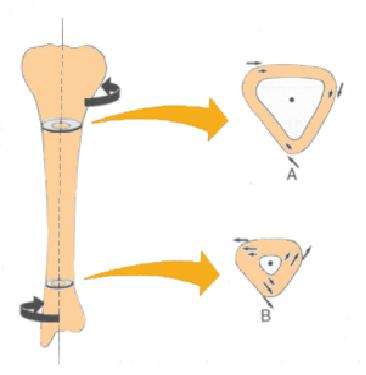
(ID 1916)
Modulo de elasticidad del hueso

(ID 1690)
ID:(322, 0)
