(ID 1909)

Die Beziehung zwischen die Federkraft ($F_k$) und der Dehnung die Verlängerung ($u$) wird als Hooke'sches Gesetz ausgedr ckt und bezeichnet. Die Konstante die Hookes Konstante ($k$) wird als die Federkonstante bezeichnet:

(ID 3207)

(ID 1908)

(ID 1907)

Wenn Sie das Verhalten eines Festk rpers unter Einwirkung einer Kraft modellieren m chten, k nnen Sie zun chst das Verhalten einer Teileinheit in Betracht ziehen, wie zum Beispiel zwei hintereinander geschaltete Federn, wie in der Abbildung gezeigt:

Diese Art der Anordnung der Federn wird als in Serie bezeichnet. Sie zeichnet sich dadurch aus, dass die Kraft die Kraft ($F$) in beiden Federn gleich ist und sie sich gem die Hookes Konstante ($k$) verformen. Daher wird die quivalente Federkonstante die Verlängerung ($u$) als Summe von die Federdehnung 1 ($u_1$) und die Federdehnung 2 ($u_2$) berechnet, die wiederum nach dem Hooke'schen Gesetz:

gleich die Kraft ($F$) geteilt durch die Konstanten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) ist:

$u = u_1 + u_2 = \displaystyle\frac{F}{k_1} + \displaystyle\frac{F}{k_2} = \left(\displaystyle\frac{1}{k_1} + \displaystyle\frac{1}{k_2}\right)F$

Daher kann das System aus zwei Federn als eine einzige Feder behandelt werden, deren quivalente Federkonstante die Insgesamt Haken Constant von Federn in Serie ($k_s$) wie folgt berechnet wird:

(ID 1910)

In dem Fall von zwei Widerst nden mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), wenn sie parallel geschaltet sind, verhalten sie sich so, als ob es einen quivalenten Widerstand die Insgesamt Haken Constant von Federn in Serie ($k_s$) g be, der gem der folgenden Gleichung berechnet wird:

Dieses Konzept kann f r die Hook Konstant der Feder i ($k_i$) wie folgt verallgemeinert werden:

(ID 3208)

Wenn wir zwei Widerst nde mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) in Serie schalten, addieren sich die Dehnungen, wodurch jeder einzelne Widerstand basierend auf seinem Kehrwert wirkt. Auf diese Weise ist der Kehrwert von die Insgesamt Haken Constant von Federn in Serie ($k_s$) gleich der Summe der Kehrwerte der individuellen Konstanten die Hook Konstant der Feder i ($k_i$):

(ID 3753)

$\displaystyle\frac{1}{k_s}=\displaystyle\frac{1}{k_1}+\displaystyle\frac{1}{k_2}+\displaystyle\frac{1}{k_3}$

(ID 3754)

Wenn man modellieren m chte, wie sich ein Festk rper unter dem Einfluss einer Kraft verformt, kann man zun chst das Verhalten einer Teilkomponente betrachten, wie zum Beispiel zwei Federn, die nebeneinander verbunden sind, wie in der Abbildung gezeigt:

Diese Art der Anordnung der Federn wird als parallel bezeichnet. Sie zeichnet sich dadurch aus, dass die Verlängerung ($u$) in beiden Federn gleich ist und jede Feder ERROR:4975,0 gem die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) nach dem Hooke'schen Gesetz beitr gt:

Daraus folgt:

$F = F_1 + F_2 = k_1 u + k_2 u = (k_1 + k_2)u$

Daher kann das System aus zwei Federn als eine einzige Feder behandelt werden, deren quivalente Federkonstante die Gesamte Hook-Konstante paralleler Federn ($k_p$) wie folgt berechnet wird:

(ID 1692)

Im Fall von zwei Federn mit den Konstanten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), die durch eine einzige Feder mit einer Konstanten die Gesamte Hook-Konstante paralleler Federn ($k_p$) modelliert werden k nnen, die mithilfe der folgenden Gleichung berechnet wird:

F r den allgemeineren Fall von Federn mit Konstanten ERROR:10228,0 kann die Gleichung wie folgt verallgemeinert werden:

Dies erm glicht es uns, eine Makrostruktur wie folgt zu modellieren:

(ID 1684)

F r den Fall von zwei Widerst nden mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$), wenn sie parallel geschaltet sind, verhalten sie sich so, als g be es einen quivalenten Widerstand die Gesamte Hook-Konstante paralleler Federn ($k_p$), der durch die folgende Gleichung gegeben ist:

Dieses Konzept kann f r die Hook Konstant der Feder i ($k_i$) verallgemeinert werden als:

(ID 3756)

Wenn Sie zwei Widerst nde mit den Werten die Hook Konstant der Feder 1 ($k_1$) und die Hook Konstant der Feder 2 ($k_2$) parallel schalten, addieren sich ihre Effekte, sodass sie sich wie ein quivalenter Widerstand die Gesamte Hook-Konstante paralleler Federn ($k_p$) verhalten, der gleich der Summe der individuellen Konstanten ist:

(ID 3757)

$k_p=k_1+k_2+k_3$

(ID 3758)

(ID 738)

Der Knochen kann als Hohlzylinder modelliert werden, da das Material im Inneren keine bedeutende Last tragen kann. Daher wird er geometrisch als Zylinder mit den Eigenschaften der Körperlänge ($L$), der Inner Radius ($R_1$) und der Außenwerbung Radio ($R_2$) dargestellt:

None

Daher ist der Wirkungsradius ($R$)

die Körper Sektion ($S$) ist

und der Trägheitsmoment der Fläche ($I_s$) ist

(ID 1915)

Mikroskopische elastische Verformung entspricht einer Modifikation des Abstands zwischen den Atomen unter einer externen Kraft, ohne dass eine Neuordnung dieser Atome erfolgt.

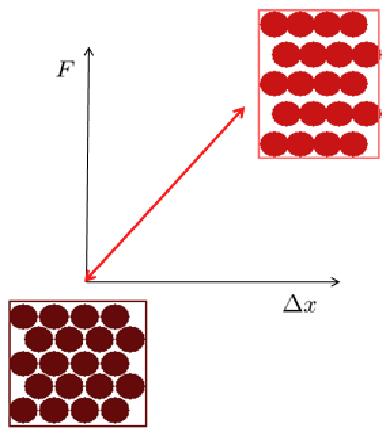
None

Im Allgemeinen handelt es sich um eine Verformung, bei der der Abstand proportional zur angewandten Kraft ver ndert wird, und man spricht von einer elastischen Verformung.

(ID 1685)

$k_p=Nk$

(ID 3759)

Um die makroskopische quivalente der mikroskopischen Federkonstanten zu berechnen, m ssen alle Mikrofedern sowohl in Reihe als auch parallel addiert werden. Daf r muss man insbesondere die Anzahl der in Parallel geschalteten Federn kennen.

Die Anzahl der in Parallel geschalteten Federn kann mit die Körper Sektion ($S$) und die Mikroskopische Abschnitt des Frühlings ($s$) bestimmt werden. Der Anzahl der Federn in Parallel ($N_p$) wird durch die Division von die Körper Sektion ($S$) durch die Mikroskopische Abschnitt des Frühlings ($s$) berechnet:

(ID 3760)

$k_s=\displaystyle\frac{k}{N}$

(ID 3755)

Um die makroskopische quivalente der mikroskopischen Federkonstante zu berechnen, m ssen alle Mikrofedern sowohl in Parallel- als auch in Reihenschaltung addiert werden. Daf r ist es erforderlich, insbesondere die Anzahl der in Serie geschalteten Federn zu kennen.

Wenn wir der Anzahl der Federn in Serie ($N_s$) sch tzen m chten, gen gt es, der Körperlänge ($L$) und der Mikroskopische Länge des Frühlings ($l$) zu kennen. Der Anzahl der Federn in Serie ($N_s$) wird durch Division von der Körperlänge ($L$) durch der Mikroskopische Länge des Frühlings ($l$) berechnet:

(ID 3761)

F r eine Stange mit ERROR:5355.1 und die Körper Sektion ($S$) k nnen Sie der Anzahl der Federn in Parallel ($N_p$) und der Anzahl der Federn in Serie ($N_s$) mit der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) berechnen. Mit diesen Werten k nnen Sie die Federkonstante f r einen gesamten Abschnitt berechnen, indem Sie mit der Anzahl der Federn in Parallel ($N_p$) und die Mikroskopische Hook-Konstante ($k_m$) multiplizieren. Auf diese Weise k nnen Sie die Hookes Konstante ($k$) berechnen, indem Sie den erhaltenen Wert durch der Anzahl der Federn in Serie ($N_s$) teilen:

$k=\displaystyle\frac{k_p}{N_s}=\displaystyle\frac{N_p}{N_s}k_m$

Wenn Sie die Ausdr cke f r die Anzahl der Elemente mit der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) einf hren, erhalten Sie den folgenden Ausdruck:

(ID 3205)

Der Ausdruck f r die Hookes Konstante ($k$) gegeben durch

hat zwei makroskopische Parameter, n mlich der Körperlänge ($L$) und die Körper Sektion ($S$). Die brigen die Mikroskopische Hook-Konstante ($k_m$), der Mikroskopische Länge des Frühlings ($l$) und die Mikroskopische Abschnitt des Frühlings ($s$) sind mikroskopisch und h ngen daher vom beschriebenen Material ab. Daher macht es Sinn, diese Faktoren als der Elastizitätsmodul ($E$) zu definieren, sodass:

(ID 3204)

Da das Hookesche Gesetz die Federkraft ($F_k$) durch die Hookes Konstante ($k$) und die Verlängerung ($u$) auf folgende Weise in Beziehung setzt:

kann man die Hookes Konstante ($k$) durch den mikroskopischen Ausdruck ersetzen und unter Verwendung der Definition von der Elastizitätsmodul ($E$) ergibt sich mit der Körperlänge ($L$) und die Körper Sektion ($S$), dass:

(ID 3209)

Die Federkraft ($F_k$) ist eine Funktion von der Elastizitätsmodul ($E$), die Körper Sektion ($S$), die Verlängerung ($u$) und der Körperlänge ($L$).

In diesem Fall wird das Verh ltnis zwischen die Verlängerung ($u$) und der Körperlänge ($L$) durch die Verformung ($\epsilon$) dargestellt, das wie folgt definiert werden kann:

(ID 3762)

Die Federkraft ($F_k$) ist eine Funktion, die von der Elastizitätsmodul ($E$), die Körper Sektion ($S$), die Verlängerung ($u$) und der Körperlänge ($L$) abh ngt.

Ebenso, genau wie die Verformung ($\epsilon$) eingef hrt wird, um die Verwendung der Dimension der Körperlänge ($L$) zu vermeiden, k nnen wir einen Faktor konstruieren, der die Federkraft ($F_k$) in Abh ngigkeit von die Körper Sektion ($S$) als die Spannung ($\sigma$) ausdr ckt.

(ID 3210)

Das Hookesche Gesetz f r ERROR:8845, ERROR:8843 und ERROR:8838 ist wie folgt ausgedr ckt:

Dieses Gesetz kann f r die Spannung auf der Achse $i$ ($\sigma_i$) und die Verformung in der Koordinaten $i$ ($\epsilon_i$) wie folgt verallgemeinert werden:

(ID 3764)

Im Allgemeinen wird die Verformung ($\epsilon$) als die Ver nderung von die Verlängerung ($u$) im Verh ltnis zu der Körperlänge ($L$) definiert:

Dieses Konzept kann im mikroskopischen Grenzwert verallgemeinert werden, indem die Verformung in der Koordinaten $i$ ($\epsilon_i$) als die Variation der Verschiebung in i ($\partial u_i$) ber der Länge eines Elements in i ($\partial x_i$) in Richtung $i$ eingef hrt wird, und es w rde wie folgt ausgedr ckt:

Der Grund f r die Verwendung eines anderen Symbols, um das Differential auszudr cken

$d \rightarrow \partial$

ist, dass es verschiedene Differentiale gibt, die verschiedene Variablen im Modell beeinflussen. Die Verwendung des Symbols $\partial$ zeigt an, dass eine Variation nach der anderen durchgef hrt werden sollte, was bedeutet, dass bei Betrachtung einer Variable die verbleibenden Variablen ihre Anfangswerte annehmen.

(ID 3763)

Bei Scherung geht die Verformung nicht mit einer Dehnung oder Stauchung einher, sondern mit einem seitlichen Versatz der W rfelfl chen. Die Scherung wird daher durch den Winkel \gamma beschrieben, mit dem es m glich ist, die Fl che senkrecht zu den verschobenen Fl chen zu drehen. In Analogie zum Hook'schen Gesetz f r Stauchung und Dehnung haben wir den Zusammenhang zwischen Torsion \tau und Winkel \gamma:

wobei G der sogenannte Schubmodul ist.

(ID 3771)

Mit der Außenwerbung Radio ($R_2$) und der Inner Radius ($R_1$), ist die Körper Sektion ($S$) definiert als

(ID 3784)

Plastische Verformung bedeutet, dass sich das Material bei Reduzierung der angelegten Spannung zwar weniger verformt, aber eine bleibende Verformung aufweist.

None

Daher kehrt es bei erneuter Belastung in der Regel in seine elastische Form zur ck, kann jedoch aufgrund der neuen Form nicht seine urspr ngliche Form wiedererlangen.

(ID 1911)

Eine m gliche Situation ist, dass eine Verformungskraft mit zwei Fixpunkten ($F_2$) auf einen Knochen mit den Eigenschaften ein Körperlänge ($L$), der Elastizitätsmodul ($E$) und der Trägheitsmoment der Fläche ($I_s$) wirkt, der an beiden Enden fixiert ist:

None

die Dehnungsenergie mit zwei Fixpunkten ($W_2$), der die Struktur gegen ein Bewegung in Flexion mit zwei Fixpunkten ($u_2$) speichert, ist gegeben durch

die Verformungskraft mit zwei Fixpunkten ($F_2$), die angewendete Kraft, f hrt zu ein Bewegung in Flexion mit zwei Fixpunkten ($u_2$) gem

und die Spannung zur Verformung mit zwei Fixpunkten ($\sigma_2$), das von der Außenwerbung Radio ($R_2$) abh ngt, ist ausgedr ckt als

(ID 740)

$T=\displaystyle\frac{I_sG}{L}\gamma$

(ID 3773)

Ein m gliches Szenario ist, dass eine Verformungskraft im Knickzustand ($F_p$) entlang der Achse des Knochens mit den Eigenschaften ein Körperlänge ($L$), der Elastizitätsmodul ($E$), der Knickfaktor ($K$), der Wirkungsradius ($R$) und der Trägheitsmoment der Fläche ($I_s$) wirkt und dadurch ein Knicken verursacht:

None

die Dehnungsenergie im Knickzustand ($W_p$), wird definiert als

die Verformungskraft im Knickzustand ($F_p$), die angewendete Kraft, f hrt gem

und die Verformungsspannung bei Knickung ($\sigma_p$), das von der Außenwerbung Radio ($R_2$) abh ngt, wird ausgedr ckt als

(ID 741)

Plastische Verformung bedeutet, dass sich Atome neu ordnen, sich von bestehenden Strukturen l sen und neue Bindungen bilden, die an sich stabil sind. Diese Verformung f hrt jedoch in der Regel zu einer Modifikation der Form des Materials.

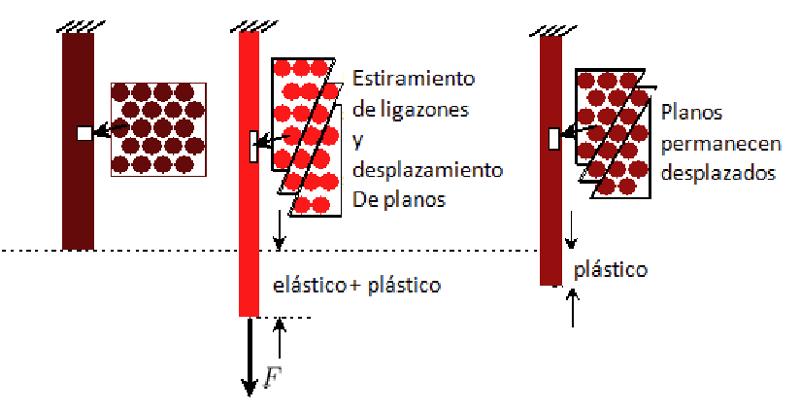
None

Plastische Verformung kann letztendlich zu Ver nderungen f hren, die katastrophale Br che einschlie en k nnen, die permanent sind.

(ID 1686)

Die seitliche Verformung steht direkt im Verh ltnis zur Verformung, die sie verursacht. Der Proportionalit tskoeffizient wird als der Poisson Koeffizient ($\nu$) [1] bezeichnet und liegt normalerweise im Bereich von 0,15 bis 0,4.

Wenn die urspr ngliche Verformung die Verformung ($\epsilon$) betr gt und die erzeugte Verformung die Verformung in Richtung senkrecht zur Kraft ($\epsilon_{\perp}$) ist, ergibt sich folgende Beziehung:

In der linearen N herung repr sentiert der Poisson'sche Koeffizient das Verh ltnis zwischen seitlichen und longitudinalen Verformungen.

wobei das Vorzeichen darauf hinweist, dass die Verformung in entgegengesetzter Richtung zur Ursache erfolgt.

[1] Dieses Konzept wurde von Sim on Denis Poisson in einer Arbeit zur statistischen Analyse eingef hrt, in der er unter anderem Themen behandelt, die nichts mit Mechanik zu tun haben. Er erw hnt darin, was sp ter als der Poisson'sche Koeffizient in einem Beispiel zur Elastizit t bezeichnet wurde. Die Arbeit tr gt den Titel "Recherches sur la Probabilit des Jugements en Mati re Criminelle et en Mati re Civile" (Forschungen zur Wahrscheinlichkeit von Urteilen in Straf- und Zivilsachen), verfasst von Sim on Denis Poisson (1837).

(ID 3765)

Der Trägheitsmoment der Fläche ($I_s$) wird im Fall eines Zylinders mit der Außenwerbung Radio ($R_2$) und der Inner Radius ($R_1$) durch

(ID 3774)

Eine Situation, die auftreten kann, ist, wenn eine Verformungskraft mit Fixpunkt ($F_1$) auf einen Knochen mit den Eigenschaften ein Körperlänge ($L$), der Elastizitätsmodul ($E$) und der Trägheitsmoment der Fläche ($I_s$) wirkt, der an einem Ende fixiert ist.

None

die Dehnungsenergie mit Fixpunkt ($W_1$), der die Struktur gegen eine Spannung zur Verformung mit einem festen Punkt ($\sigma_1$) speichert, ist definiert durch

die Verformungskraft mit Fixpunkt ($F_1$), die angewendete Kraft, f hrt zu eine Spannung zur Verformung mit einem festen Punkt ($\sigma_1$) gem

und die Spannung zur Verformung mit einem festen Punkt ($\sigma_1$), das von der Außenwerbung Radio ($R_2$) abh ngt, ist gegeben durch

(ID 739)

Eine M glichkeit, einen Knochenbruch zu verursachen, ist durch Knochenverdrehung, was das Anwenden entgegengesetzter Drehmomente an den Enden beinhaltet:

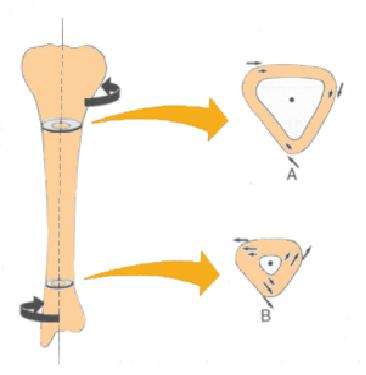
(ID 1916)

(ID 1690)