Usuario:
Tensiones en torno a la punta de un quiebre
Nota 
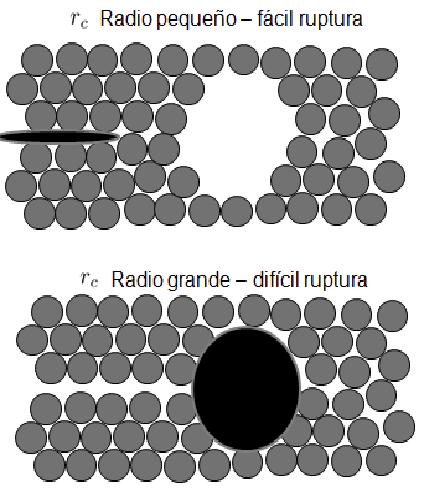
La propagación de la fractura se produce porque la punta de ésta tiene un radio extremadamente pequeño, lo que implica una tensión muy alta, ya que ésta es proporcional al inverso de la raíz cuadrada del radio.
El avance de la fractura puede detenerse si en algún momento el radio aumenta, reduciendo la tensión en la punta. Esto se logra, por ejemplo, mediante la porosidad del material o la inserción de inhomogeneidades que actúan como un punto de concentración de tensión.
None
ID:(1691, 0)
Ruptura de Huesos
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
The breaking stress is proportional to the el factor de intensidad ($K_I$), which is proportional to the square root of la fuerza ($F$), el módulo de Elasticidad ($E$), and el largo de quiebre ($l$):
| $ K_I =\sqrt{\displaystyle\frac{ F E }{ l }}$ |
(ID 3785)
Da o por flexi n
(ID 1919)
Da o por compresi n
(ID 1918)
La tensi n en la punta del quiebre es proporcional al factor de intensidad
| $ \sigma_y =\displaystyle\frac{ K_i }{\sqrt{2 \pi r_p }}$ |
(ID 3786)
La tensi n en la direcci n paralela
| $\sigma_x(r,\theta)=\displaystyle\frac{K_i}{\sqrt{2pi r}}\cos\displaystyle\frac{\theta}{2}\left(1-\sin\displaystyle\frac{\theta}{2}\sin\displaystyle\frac{3\theta}{2} \right)$ |
(ID 3788)
La tensi n en la direcci n perpendicular
| $ \sigma_y =\displaystyle\frac{ K_i }{\sqrt{2 \pi r }}\cos\displaystyle\frac{\theta}{2}\left(1-\sin\displaystyle\frac{ \theta }{2}\sin\displaystyle\frac{3 \theta }{2}\right)$ |
(ID 3787)
La propagaci n de la fractura se produce porque la punta de sta tiene un radio extremadamente peque o, lo que implica una tensi n muy alta, ya que sta es proporcional al inverso de la ra z cuadrada del radio.
El avance de la fractura puede detenerse si en alg n momento el radio aumenta, reduciendo la tensi n en la punta. Esto se logra, por ejemplo, mediante la porosidad del material o la inserci n de inhomogeneidades que act an como un punto de concentraci n de tensi n.
None
(ID 1691)
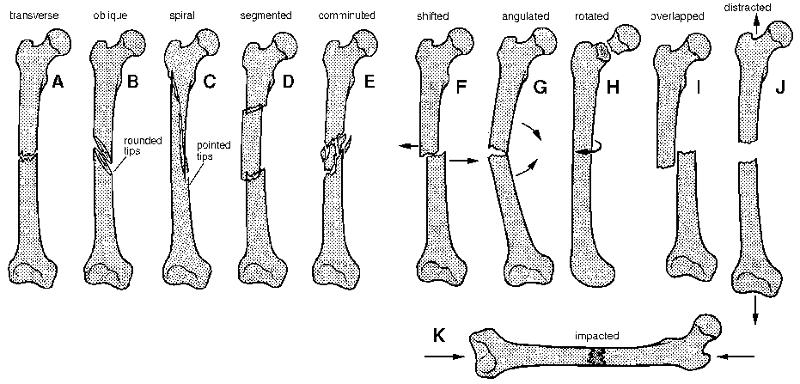
Distintos mecanismos de ruptura
(ID 1917)
ID:(323, 0)