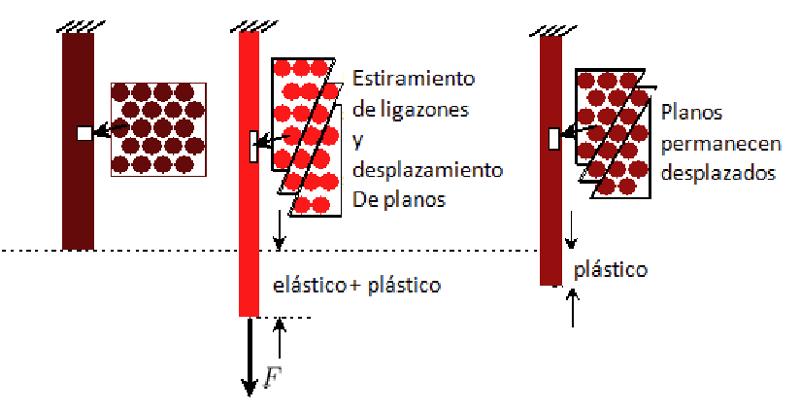
Deformación plástica
Storyboard 
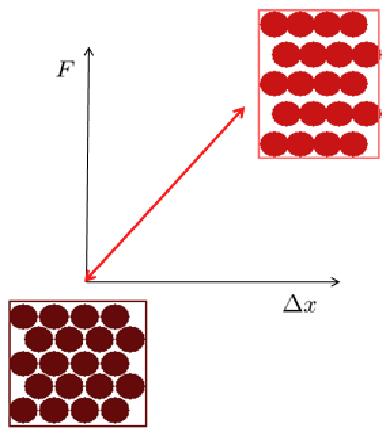
Para pequeñas deformaciones, el material solo sufre una deformación elástica, es decir, al retirar la carga este vuelve a su forma original. Para deformaciones mayores, los átomos pueden sufrir desplazamientos mayores, cambiando la estructura de forma permanente. En estos casos hablamos de deformación plástica.
ID:(324, 0)
Deformación plástica
Storyboard 
Para pequeñas deformaciones, el material solo sufre una deformación elástica, es decir, al retirar la carga este vuelve a su forma original. Para deformaciones mayores, los átomos pueden sufrir desplazamientos mayores, cambiando la estructura de forma permanente. En estos casos hablamos de deformación plástica.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
El hueso se puede modelar como un cilindro hueco, ya que el material en su interior no es capaz de soportar una carga significativa. Por lo tanto, se modela geom tricamente como un cilindro con propiedades el largo del cuerpo ($L$), el radio interior ($R_1$) y el radio exterior ($R_2$):
Por ello el radio efectivo ($R$) es
la sección del elemento ($S$) es
y el momento de inercia de superficie ($I_s$) es
En el caso del hueso se tiene distintas situaciones que llevan a que se generen tensiones extremas que conducen a la ruptura.
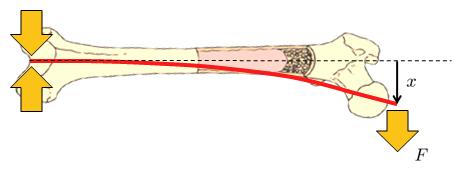
Una situaci n es el caso en que el hueso est fijo en un extremo y es flexionado desde el otro:
Un ejemplo es una persona que cae y se apoya en un punto, creando un punto fijo por roce mientras el centro de masa contin a desplaz ndose por inercia, flexionando el hueso hasta el punto en que se fractura.
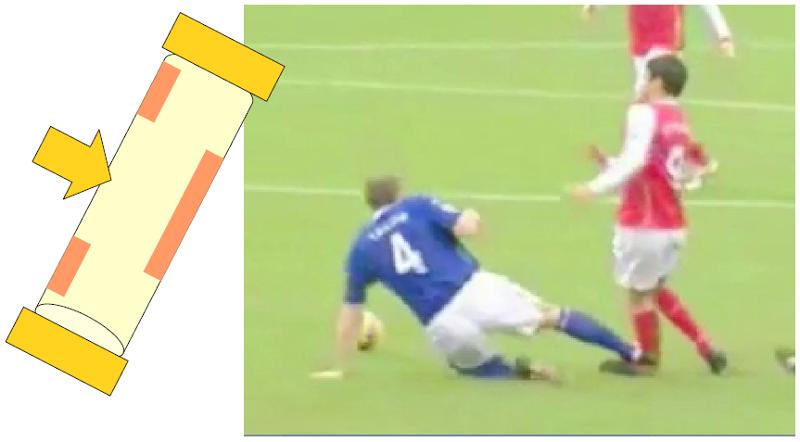
Otra variante es que est fijo en ambos extremos y reciba una fuerza perpendicular en alguna posici n intermedia:
Un ejemplo t pico de esto es cuando un futbolista apoya el pie (un punto fijo) y la masa de su cuerpo, por inercia, retiene el segundo punto que se puede considerar fijo, mientras otro jugador impacta con su pie la pierna del jugador.
Por ltimo, existe la situaci n en que el hueso colapsa por presi n axial.
En este caso, existen dos situaciones. Por un lado, puede colapsar la estructura misma del hueso y fracturarse por compresi n. Por el otro lado, puede existir pandeo, es decir, por alguna inhomogeneidad se flexiona el hueso y termina deflej ndose en forma extrema, llevando a la fractura.
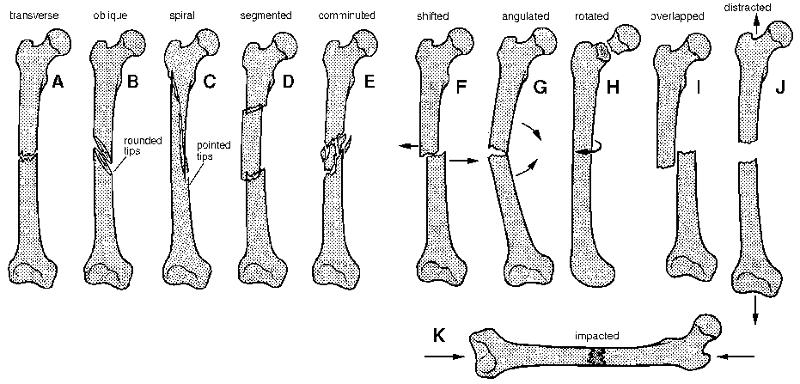
Estos son los mecanismos b sicos que luego, en la realidad, pueden iniciar el proceso comprometiendo otros huesos o extendi ndose en el mismo hueso, generando una ruptura m s compleja.
Una situaci n que puede ocurrir es que una fuerza de deformación con un punto fijo ($F_1$) act e sobre un hueso de un largo del cuerpo ($L$), el módulo de Elasticidad ($E$) y el momento de inercia de superficie ($I_s$) que est fijo en un extremo.
la energía de deformación con un punto fijo ($W_1$), que almacena la estructura ante una tensión para deformación con un punto fijo ($\sigma_1$), es
la fuerza de deformación con un punto fijo ($F_1$), que se aplica, lleva a una tensión para deformación con un punto fijo ($\sigma_1$), seg n
y la tensión para deformación con un punto fijo ($\sigma_1$), que depende de el radio exterior ($R_2$), es
Una situaci n que puede ocurrir es que una fuerza de deformación con dos puntos fijos ($F_2$) act e sobre un hueso con las propiedades un largo del cuerpo ($L$), el módulo de Elasticidad ($E$) y el momento de inercia de superficie ($I_s$), que est fijo en ambos extremos:
la energía de deformación con dos puntos fijos ($W_2$), que almacena la estructura frente a un desplazamiento en flexión con dos puntos fijos ($u_2$), es
la fuerza de deformación con dos puntos fijos ($F_2$), que se aplica, lleva a un desplazamiento en flexión con dos puntos fijos ($u_2$), seg n
y la tensión para deformación con dos puntos fijos ($\sigma_2$), que depende de el radio exterior ($R_2$), es
Una situaci n que puede ocurrir es que una fuerza de deformación en condición de pandeo ($F_p$) act e a lo largo del eje del hueso con las propiedades un largo del cuerpo ($L$), el módulo de Elasticidad ($E$), el factor de pandeo ($K$), el radio efectivo ($R$) y el momento de inercia de superficie ($I_s$), generando pandeo:
la energía de deformación en condición de pandeo ($W_p$), se define como
la fuerza de deformación en condición de pandeo ($F_p$), la fuerza aplicada, seg n
y la tensión para deformación en el caso de pandeo ($\sigma_p$), que depende de el radio exterior ($R_2$), se expresa como
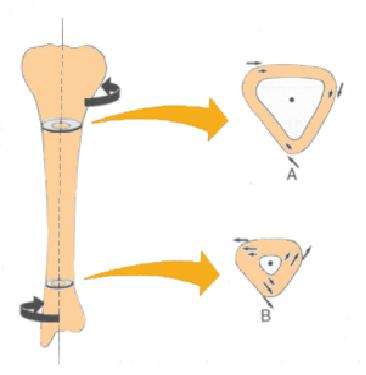
Una de las formas de generar una fractura es mediante la torsi n del hueso, que implica la aplicaci n de torques opuestos en los extremos:
La deformaci n el stica microsc pica corresponde a una modificaci n de la distancia entre los tomos bajo una fuerza externa, sin que ocurra un reordenamiento de estos.
En general, es una deformaci n en la que la distancia se modifica de manera proporcional a la fuerza aplicada, y se habla de una deformaci n el stica.
La deformaci n pl stica implica que si se reduce la tensi n aplicada, el material disminuye su deformaci n pero termina con una deformaci n permanente.
Por lo tanto, si se somete nuevamente a tensi n, por lo general vuelve a su forma el stica, pero debido a la nueva forma, no puede recuperar su forma original.
Una deformaci n pl stica implica que los tomos se reordenen, disoci ndose de estructuras existentes y formando nuevas uniones que son estables en s mismas. Sin embargo, dicha deformaci n generalmente implica una modificaci n en la forma del medio.
La deformaci n pl stica puede finalmente llevar a modificaciones que incluyen rupturas catastr ficas que son permanentes.
Trabajaremos con un hueso y con los escenarios de ca da y de golpe. Los par metros del hueso y de las propiedades del material se resumen aqu :
Si un jugador recibe un impacto en la mitad del hueso y se considera que el pie, debido a la fricci n, y el cuerpo, debido a la inercia, son puntos fijos, se genera una carga que flexiona el hueso.
Pregunta de inter s: Cu l es la energ a, la tensi n, la fuerza, el desplazamiento y la altura de salto en los que se presentar a el pandeo? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
Se consideran dos situaciones, la ca da (quiebre por pandeo, compresi n o flexi n) e impacto en la parte central del hueso (quiebre por flexi n).
La integraci n sobre la secci n con el radio interior ($R_1$) y el radio exterior ($R_2$) conduce a la introducci n de el radio efectivo ($R$), definido por:
Con el radio exterior ($R_2$) y el radio interior ($R_1$), la sección del elemento ($S$) est definido por
El momento de inercia de superficie ($I_s$) se calcula en el caso de un cilindro con el radio exterior ($R_2$) y el radio interior ($R_1$) mediante
La relaci n entre la energía de deformación con dos puntos fijos ($W_2$) y el desplazamiento en flexión con dos puntos fijos ($u_2$) en una flexi n con dos puntos fijos depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$), y el momento de inercia de superficie ($I_s$) es
La relaci n entre la fuerza de deformación con dos puntos fijos ($F_2$) y el desplazamiento en flexión con dos puntos fijos ($u_2$) en una flexi n con dos puntos fijos depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$) y el momento de inercia de superficie ($I_s$). En este contexto,
La relaci n entre la tensión para deformación con dos puntos fijos ($\sigma_2$) y la fuerza de deformación con dos puntos fijos ($F_2$) en una flexi n con dos puntos fijos depende de el radio exterior ($R_2$), el largo del cuerpo ($L$) y el momento de inercia de superficie ($I_s$). En este contexto,
La relaci n entre la energía de deformación con un punto fijo ($W_1$) y el desplazamiento en flexión con un punto fijo ($u_1$) en una flexi n con un punto fijo depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$) y el momento de inercia de superficie ($I_s$) es:
La relaci n entre la fuerza de deformación con un punto fijo ($F_1$) y el desplazamiento en flexión con un punto fijo ($u_1$) en una flexi n con un punto fijo depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$) y el momento de inercia de superficie ($I_s$). En este contexto,
La relaci n entre la tensión para deformación con un punto fijo ($\sigma_1$) y la fuerza de deformación con un punto fijo ($F_1$) en una flexi n con un punto fijo depende de el radio exterior ($R_2$), el largo del cuerpo ($L$) y el momento de inercia de superficie ($I_s$) es
La energía de deformación en condición de pandeo ($W_p$) en pandeo depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$), el momento de inercia de superficie ($I_s$), el radio efectivo ($R$) y el factor de pandeo ($K$) es
El valor de el factor de pandeo ($K$) es igual a:
• 0.5 si ambos bordes est n fijos,
• 1.0 si ambos pueden rotar,
• 0.7 si uno est fijo y el otro puede rotar, y
• 2.0 si ambos est n libres.
La fuerza de deformación en condición de pandeo ($F_p$) en pandeo depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$), el momento de inercia de superficie ($I_s$) y el factor de pandeo ($K$).
El valor de el factor de pandeo ($K$) es igual a:
• 0.5 si ambos bordes est n fijos,
• 1.0 si ambos pueden rotar,
• 0.7 si uno est fijo y el otro puede rotar, y
• 2.0 si ambos est n libres.
La tensión para deformación en el caso de pandeo ($\sigma_p$) en pandeo depende de el módulo de Elasticidad ($E$), el largo del cuerpo ($L$), el momento de inercia de superficie ($I_s$), la sección del elemento ($S$) y el factor de pandeo ($K$).
El valor de el factor de pandeo ($K$) es igual a:
• 0.5 si ambos bordes est n fijos,
• 1.0 si ambos pueden rotar,
• 0.7 si uno est fijo y el otro puede rotar, y
• 2.0 si ambos est n libres.
ID:(324, 0)