Storyboard

Die Mikroporosität des Bodens hängt von seiner Zusammensetzung ab, daher ist es wichtig, sie basierend auf dem Anteil der verschiedenen Komponenten modellieren zu können. Hierzu wird zunächst der volumetrische Faktor der verschiedenen Texturen untersucht, und dann wird die Porosität unter Berücksichtigung einer grundlegenden Komponente, die von Ton bereitgestellt wird, abgeschätzt. Darüber hinaus wird die Anwesenheit von Sand und Schluff berücksichtigt, jedoch ist es wichtig zu beachten, dass Ton in die Zwischenräume zwischen den Körnern eindringen kann, was die Gesamtporosität reduziert.

>Modell

ID:(2050, 0)

Konzept

>Top

ID:(15199, 0)

Konzept

>Top

Im Fall von Böden im Allgemeinen können wir das Bodentextur-Dreieck studieren. Wenn wir den typischen Bereich der Porosität für jeden Bodentyp beschreiben, können wir sehen, was zuvor diskutiert wurde. In der Ecke, in der Sand vorherrscht, haben wir eine Porosität, die bis zu 25% erreichen kann, was für ein Modell von Kugeln optimal ist:

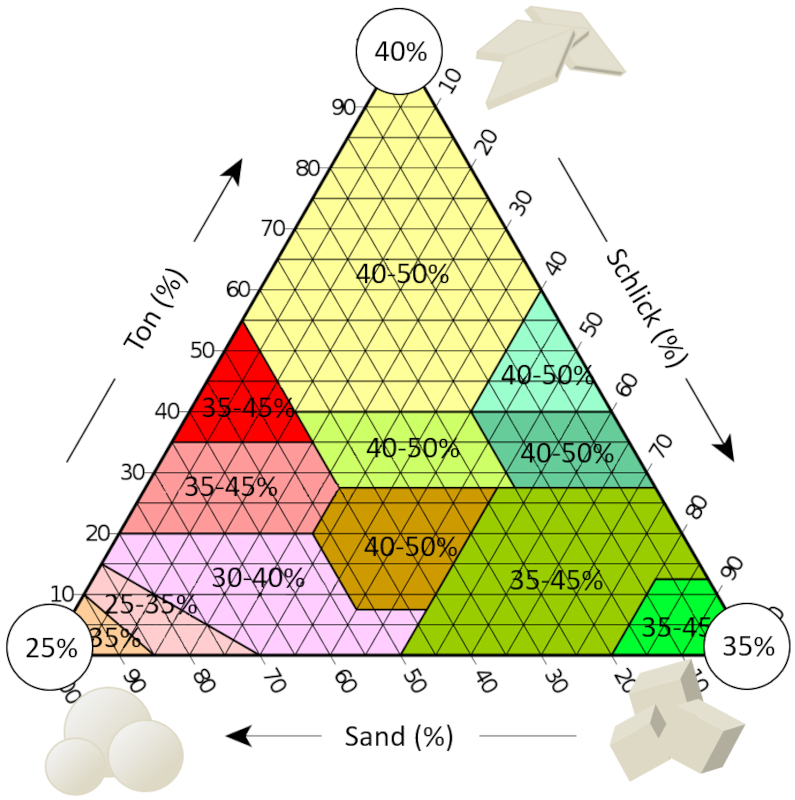
Texturdreieck, das den aus [1] und [2] ermittelten Porositätsbereich umfasst.

Wenn wir jetzt die Ecke des Schluffs betrachten, sehen wir, dass eine Porosität von 35% erreicht werden kann, was dem Raum entspricht, der von Würfeln nicht gefüllt werden kann. Das bedeutet, dass das Material nicht in der Lage ist, sich so anzuordnen, dass es die kubische Struktur optimal ausnutzt. Dies ist wahrscheinlich eine Folge von attraktiven Kräften auf der Mikronskala, die zu einer ungeordneten Stapelung führen.

Im letzten Fall können wir die Grenze des Tons sehen, bei dem die Porosität einen Wert von etwa 40% erreicht, was wiederum eine Folge der Wechselwirkung zwischen den Platten sein muss, die Gruppen von ihnen organisieren können, aber nicht das gesamte System.

Zusammenfassend lässt sich sagen, dass wir beobachten, dass in der unteren linken Ecke, wo der Boden hauptsächlich aus Sand besteht, die Porosität bis zu 25% erreichen kann. Diese 25% entsprechen genau der Porosität, die im besten Fall für ein Modell von Kugeln erreicht wird.

Mit anderen Worten, es gibt eine inhärente Porosität, die für Bodentypen spezifisch ist, und bei solchen mit einem signifikanten Anteil an Ton dominiert der Ton. Der Effekt von Sand und Schluff überwiegt nur in Extremfällen, in denen das Material sehr wenig Ton enthält.

[1] Soil Mechanics and Foundations, Muni Budhu, (2011), John Wiley & Sons.

[2] Principles of Geotechnical Engineering, Braja M. Das, (2010), Cengage Learning

ID:(2078, 0)

Konzept

>Top

Wenn wir annehmen, dass die Dichten der verschiedenen Bestandteile ähnlich sind:

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

können die Volumenfaktoren die Volumenanteil von Sand in der Probe ($f_a$), die Volumenanteil des Schlicks in der Probe ($f_i$), die Volumenanteil von Ton in der Probe ($f_c$) in Bezug auf die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$) wie folgt ausgedrückt werden:

$f_a = (1-f)\displaystyle\frac{\rho_s}{\rho_a}g_a \sim (1-f)g_a$

$f_i = (1-f)\displaystyle\frac{\rho_s}{\rho_i}g_i \sim (1-f)g_i$

$f_c = (1-f)\displaystyle\frac{\rho_s}{\rho_c}g_c \sim (1-f)g_c$

Dies ermöglicht uns, den Bereich der volumetrischen Faktoren für verschiedene Bodentypen abzuschätzen, einschließlich der Fälle, in denen die Porosität ($f$) und die Volumenanteil der Makroporen in der Probe ($f_m$) null sind:

ID:(15096, 0)

Beschreibung

>Top

Angesichts der vorliegenden Informationen für die Temperatur in Grad Celsius in den Zustand 2 ($t_2$), der Eigener Volumenfaktor von Sand ($p_a$), der Schlammeigener Volumenfaktor ($p_i$), der Toneigener Volumenfaktor ($p_c$), die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$), die der Gleichung genügen:

und wir kennen die Durchschnittswerte für verschiedene Bodentexturen mit ihren jeweiligen die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$), die Massenanteil von Ton in der Probe ($g_c$) und der Die Strömung durch jede Schicht ($p_p$) wie folgt:

Können wir eine Regression durchführen, um die Werte von der Die Strömung durch jede Schicht ($p_p$), der Eigener Volumenfaktor von Sand ($p_a$) und der Schlammeigener Volumenfaktor ($p_i$) zu bestimmen. Das Ergebnis ist eine Anpassung mit einem R-Quadrat von 0,974 und die Parameter lauten wie folgt:

Im Allgemeinen entspricht der Verdichtungsgrad von Sand mit einem die Eigene Porosität des Sandes ($q_a$)-Wert von etwa 25% der maximalen Verdichtung. Bei einem die Eigene Porosität des Schlicks ($q_i$)-Wert von rund 47% ist er jedoch höher als das Optimum, genauso wie die 49% für die Eigene Porosität des Ton ($q_c$). In jedem Fall sind die Faktoren eine gute Schätzung, angesichts des hohen R-Quadrats und der niedrigen p-Test-Werte für jeden Faktor, die signifikant niedriger sind als die traditionelle Schwelle von 0,05. Versuche, andere Potenzen in die Regression einzubeziehen, zeigen, dass die lineare Approximation die einzige ist, die Koeffizienten unter 0,05 liefert. Dies legt nahe, dass die Proben Verteilungen haben müssen, die keine signifikanten Mischeffekte aufweisen und einfach Summen von Komponenten wie Aggregaten sind.

ID:(15099, 0)

Konzept

>Top

Ausgewählter Parameter

Berechnungen

ID:(15218, 0)

Gleichung

>Top, >Modell

Ähnlich wie bei der Definition der Proportionen zwischen den Massen jedes Bestandteils und der Gesamtmasse können wir ein analoges System unter Verwendung von Volumina aufstellen. Mit diesem Ansatz können wir die Volumenanteil von Sand in der Probe ($f_a$) in Bezug auf das Gesamtvolumen ($V_t$) definieren. Dies ermöglicht uns, die Menge von das Festes Sandvolumen ($V_a$) im Zusammenhang mit das Gesamtvolumen ($V_t$) zu berechnen.

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

Bedingungen

Variablen

$V_a$

Festes Sandvolumen

$m^3$

$V_t$

Gesamtvolumen

$m^3$

$f_a$

Volumenanteil von Sand in der Probe

$-$

Beziehung

ID:(10369, 0)

Gleichung

>Top, >Modell

Ähnlich wie bei der Definition der Proportionen zwischen den Massen jedes Bestandteils und der Gesamtmasse können wir ein analoges System unter Verwendung von Volumina aufstellen. Mit diesem Ansatz können wir die Volumenanteil des Schlicks in der Probe ($f_i$) in Bezug auf das Gesamtvolumen ($V_t$) definieren. Dies ermöglicht uns, die Menge von das Festes Schlammvolumen ($V_i$) im Zusammenhang mit das Gesamtvolumen ($V_t$) zu berechnen.

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

Bedingungen

Variablen

$V_i$

Festes Schlammvolumen

$m^3$

$V_t$

Gesamtvolumen

$m^3$

$f_i$

Volumenanteil des Schlicks in der Probe

$-$

Beziehung

ID:(10367, 0)

Gleichung

>Top, >Modell

Ähnlich wie die Proportionen zwischen den Massen jedes Bestandteils und der Gesamtmasse definiert sind, können wir ein analoges System unter Verwendung von Volumina aufstellen. Mit diesem Ansatz können wir die Volumenanteil von Ton in der Probe ($f_c$) in Bezug auf das Gesamtvolumen ($V_t$) definieren. Dies ermöglicht uns, die Menge von das Gesamtvolumen ($V_t$) im Kontext des Gesamtvolumens zu berechnen.

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

Bedingungen

Variablen

$V_c$

Festes Tonvolumen

$m^3$

$V_t$

Gesamtvolumen

$m^3$

Beziehung

ID:(10368, 0)

Gleichung

>Top, >Modell

Ähnlich wie bei der Definition der Proportionen zwischen den Massen jedes Bestandteils und der Gesamtmasse können wir ein analoges System unter Verwendung von Volumina aufstellen. Mit diesem Ansatz können wir die Volumenanteil der Makroporen in der Probe ($f_m$) in Bezug auf das Gesamtvolumen ($V_t$) definieren. Dies ermöglicht es uns, die Menge von der Makroporenvolumen ($V_m$) im Kontext von das Gesamtvolumen ($V_t$) zu berechnen.

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

Bedingungen

Variablen

$V_t$

Gesamtvolumen

$m^3$

$V_m$

Makroporenvolumen

$m^3$

$f_m$

Volumenanteil der Makroporen in der Probe

$-$

Beziehung

ID:(15084, 0)

Gleichung

>Top, >Modell

Die Bedingung für tonige Böden basierend auf das Festes Sandvolumen ($V_a$), das Festes Schlammvolumen ($V_i$), das Festes Tonvolumen ($V_c$), der Makroporenvolumen ($V_m$), das Eigenvolumen ($V_z$) und die Eigene Porosität des Ton ($q_c$) wird wie folgt ausgedrückt:

Wenn wir die Gleichung für das Gesamtvolumen ($V_t$) in Bezug auf das Eigenvolumen ($V_z$) verwenden und durch das Gesamtvolumen ($V_t$) teilen, können wir sie in Bezug auf die Volumenanteil von Sand in der Probe ($f_a$), die Volumenanteil des Schlicks in der Probe ($f_i$), die Volumenanteil von Ton in der Probe ($f_c$) und die Volumenanteil der Makroporen in der Probe ($f_m$) wie folgt umschreiben:

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

Bedingungen

Variablen

$q_a$

Eigene Porosität des Sandes

$-$

$q_i$

Eigene Porosität des Schlicks

$-$

$q_c$

Eigene Porosität des Ton

$-$

$f_m$

Volumenanteil der Makroporen in der Probe

$-$

$f_i$

Volumenanteil des Schlicks in der Probe

$-$

$f_a$

Volumenanteil von Sand in der Probe

$-$

$f_c$

Volumenanteil von Ton in der Probe

$-$

Beziehung

Entwicklung

Mit der Gleichung des das Gesamtvolumen ($V_t$) in Bezug auf das Eigenvolumen ($V_z$) und der Makroporenvolumen ($V_m$):

$ V_t = V_m + V_z $

Ersetzen wir das Eigenvolumen ($V_z$) in Bezug auf das Festes Sandvolumen ($V_a$), das Festes Schlammvolumen ($V_i$), das Festes Tonvolumen ($V_c$), der Makroporenvolumen ($V_m$) und die Eigene Porosität des Ton ($q_c$) durch:

$ V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$

erhalten wir:

$V_t = V_a + V_i + \displaystyle\frac{1}{1-q_c}V_c+V_m$

Wenn wir diese Gleichung durch das Gesamtvolumen ($V_t$) teilen und die Definitionen von die Volumenanteil von Sand in der Probe ($f_a$)

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

für die Volumenanteil des Schlicks in der Probe ($f_i$)

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

für die Volumenanteil von Ton in der Probe ($f_c$)

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

und für die Volumenanteil der Makroporen in der Probe ($f_m$)

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

verwenden, erhalten wir die folgende Beziehung:

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

ID:(15086, 0)

Gleichung

>Top, >Modell

Der Porenvolumen ($V_p$) in einem tonigen Material, die eine Funktion des Volumens von der Makroporenvolumen ($V_m$), die Eigene Porosität des Ton ($q_c$) und das Festes Tonvolumen ($V_c$) ist:

kann umgeschrieben werden, indem die Gleichung durch das Gesamtvolumen ($V_t$) geteilt und die Gleichung in Bezug auf die Porosität ($f$), die Volumenanteil der Makroporen in der Probe ($f_m$) und die Volumenanteil von Ton in der Probe ($f_c$) ausgedrückt wird, wodurch folgendes resultiert:

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

Bedingungen

Variablen

$q_a$

Eigene Porosität des Sandes

$-$

$q_i$

Eigene Porosität des Schlicks

$-$

$q_c$

Eigene Porosität des Ton

$-$

$f$

Porosität

$-$

$f_i$

Volumenanteil des Schlicks in der Probe

$-$

$f_a$

Volumenanteil von Sand in der Probe

$-$

$f_c$

Volumenanteil von Ton in der Probe

$-$

Beziehung

Entwicklung

Die Berechnung von der Porenvolumen ($V_p$) kann mithilfe der Volumina von der Makroporenvolumen ($V_m$), das Festes Tonvolumen ($V_c$) und die Eigene Porosität des Ton ($q_c$) mit der folgenden Gleichung durchgeführt werden:

$ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $

Durch die Division dieser Gleichung durch das Gesamtvolumen ($V_t$) können wir die Porosität ($f$) verwenden

$ f =\displaystyle\frac{ V_p }{ V_t }$

zusammen mit die Volumenanteil der Makroporen in der Probe ($f_m$)

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

und die Volumenanteil von Ton in der Probe ($f_c$)

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

was sich vereinfacht zu

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

.

ID:(2074, 0)

Gleichung

>Top, >Modell

Wie die Volumenanteil von Sand in der Probe ($f_a$) in Bezug auf das Festes Sandvolumen ($V_a$) und das Gesamtvolumen ($V_t$) definiert wurde:

Daher kannst du mit die Dichte eines Sandkorns ($\rho_a$), die Festkörperdichte ($\rho_s$), die Porosität ($f$) und die Massenanteil von Sand in der Probe ($g_a$) den Faktor berechnen, indem du folgendes verwendest:

$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $

Bedingungen

Variablen

$\rho_a$

Dichte eines Sandkorns

2.63e+3

$kg/m^3$

$\rho_s$

Festkörperdichte

$kg/m^3$

$g_a$

Massenanteil von Sand in der Probe

$-$

$f$

Porosität

$-$

$f_a$

Volumenanteil von Sand in der Probe

$-$

Beziehung

Entwicklung

Um die Volumenanteil von Sand in der Probe ($f_a$) zu berechnen, können Sie die Definition mit das Festes Sandvolumen ($V_a$) und das Gesamtvolumen ($V_t$) wie folgt verwenden:

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

das Festes Sandvolumen ($V_a$) kann mit die Dichte eines Sandkorns ($\rho_a$) und die Sandtrockenmasse ($M_a$) mithilfe der Gleichung ausgedrückt werden:

$ V_a =\displaystyle\frac{ M_a }{ \rho_a }$

Für das Gesamtvolumen ($V_t$) können Sie mit das Solides Volumen ($V_s$) und der Porenvolumen ($V_p$) arbeiten, indem Sie die Gleichung verwenden:

$ V_t = V_s + V_p $

unter Verwendung des Ausdrucks für die Porosität ($f$):

$ f =\displaystyle\frac{ V_p }{ V_t }$

Mit beiden Gleichungen erhalten Sie den Ausdruck:

$V_t = \displaystyle\frac{1}{1-f} V_s$

Durch Verwendung der Definition von die Festkörperdichte ($\rho_s$) mit die Gesamttrockenmasse der Probe ($M_s$) und das Solides Volumen ($V_s$):

$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$

können Sie das Gesamtvolumen ($V_t$) wie folgt ausdrücken:

$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$

Auf diese Weise erhalten Sie den Ausdruck für die Volumenanteil von Sand in der Probe ($f_a$) als:

$f_a= \displaystyle\frac{V_a}{V_t}= \displaystyle\frac{M_a}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_a}$

was sich mit der Gleichung für die Massenanteil von Sand in der Probe ($g_a$):

$ g_a =\displaystyle\frac{ M_a }{ M_s }$

reduziert zu:

$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $

ID:(15093, 0)

Gleichung

>Top, >Modell

Wie die Volumenanteil von Sand in der Probe ($f_a$) in Bezug auf das Festes Schlammvolumen ($V_i$) und das Gesamtvolumen ($V_t$) definiert wurde:

Daher kannst du mit die Dichte eines Schluffkorns ($\rho_i$), die Festkörperdichte ($\rho_s$), die Porosität ($f$) und die Massenanteil von Schluff in der Probe ($g_i$) den Faktor berechnen, indem du folgendes verwendest:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

Bedingungen

Variablen

$\rho_i$

Dichte eines Schluffkorns

2.65e+3

$kg/m^3$

$\rho_s$

Festkörperdichte

$kg/m^3$

$g_i$

Massenanteil von Schluff in der Probe

$-$

$f$

Porosität

$-$

$f_i$

Volumenanteil des Schlicks in der Probe

$-$

Beziehung

ID:(15094, 0)

Gleichung

>Top, >Modell

Wie die Volumenanteil von Sand in der Probe ($f_a$) in Bezug auf das Festes Tonvolumen ($V_c$) und das Gesamtvolumen ($V_t$) definiert wurde:

Daher kannst du mit die Dichte eines Tonkorns ($\rho_c$), die Festkörperdichte ($\rho_s$), die Porosität ($f$) und die Massenanteil von Ton in der Probe ($g_c$) den Faktor berechnen, indem du folgendes verwendest:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

Bedingungen

Variablen

$\rho_c$

Dichte eines Tonkorns

2.8e+3

$kg/m^3$

$\rho_s$

Festkörperdichte

$kg/m^3$

$g_c$

Massenanteil von Ton in der Probe

$-$

$f$

Porosität

$-$

$f_c$

Volumenanteil von Ton in der Probe

$-$

Beziehung

ID:(15095, 0)

Gleichung

>Top, >Modell

Die Porosität ($f$) ist eine Funktion von die Volumenanteil der Makroporen in der Probe ($f_m$), die Volumenanteil von Sand in der Probe ($f_a$), die Volumenanteil des Schlicks in der Probe ($f_i$), die Volumenanteil von Ton in der Probe ($f_c$), die Eigene Porosität des Sandes ($q_a$), die Eigene Porosität des Schlicks ($q_i$) und die Eigene Porosität des Ton ($q_c$):

Durch Verwendung der Beziehungen zwischen den volumetrischen Faktoren und Massenfaktoren die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$), unter der Annahme, dass keine Makroporen vorhanden sind und die Dichten der drei Komponenten gleich sind, erhalten wir:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Bedingungen

Variablen

$q_a$

Eigene Porosität des Sandes

$-$

$q_i$

Eigene Porosität des Schlicks

$-$

$q_c$

Eigene Porosität des Ton

$-$

$g_a$

Massenanteil von Sand in der Probe

$-$

$g_i$

Massenanteil von Schluff in der Probe

$-$

$g_c$

Massenanteil von Ton in der Probe

$-$

$f$

Porosität

$-$

Beziehung

Entwicklung

Die Porosität ($f$) ist eine Funktion von der Anzahl der Schluffkörner in der Probe ($N_i$), die Volumenanteil von Sand in der Probe ($f_a$), die Volumenanteil des Schlicks in der Probe ($f_i$), die Volumenanteil von Ton in der Probe ($f_c$), die Eigene Porosität des Sandes ($q_a$), die Eigene Porosität des Schlicks ($q_i$) und die Eigene Porosität des Ton ($q_c$):

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

Angesichts der Tatsache, dass mit die Festkörperdichte ($\rho_s$), die Dichte eines Sandkorns ($\rho_a$) und die Massenanteil von Sand in der Probe ($g_a$) gilt:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

und mit die Dichte eines Schluffkorns ($\rho_i$) und die Massenanteil von Schluff in der Probe ($g_i$) gilt:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

Darüber hinaus, mit die Dichte eines Tonkorns ($\rho_c$) und die Massenanteil von Ton in der Probe ($g_c$) gilt:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

ist es möglich, im Fall, dass die Dichten gleich sind:

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

und Makroporen nicht existieren:

$f_m\sim 0$

die folgende Beziehung zu erhalten:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

ID:(10370, 0)

Gleichung

>Top, >Modell

Mit die Eigene Porosität des Sandes ($q_a$) kann man der Eigener Volumenfaktor von Sand ($p_a$) wie folgt definieren:

$ p_a = \displaystyle\frac{ q_a }{1- q_a }$

Bedingungen

Variablen

$q_a$

Eigene Porosität des Sandes

$-$

$p_a$

Eigener Volumenfaktor von Sand

$-$

Beziehung

ID:(15087, 0)

Gleichung

>Top, >Modell

Mit die Eigene Porosität des Schlicks ($q_i$) kann man der Schlammeigener Volumenfaktor ($p_i$) wie folgt definieren:

$ p_i = \displaystyle\frac{ q_i }{1- q_i }$

Bedingungen

Variablen

$q_i$

Eigene Porosität des Schlicks

$-$

$p_i$

Schlammeigener Volumenfaktor

$-$

Beziehung

ID:(15088, 0)

Gleichung

>Top, >Modell

Mit die Eigene Porosität des Ton ($q_c$) kann man der Toneigener Volumenfaktor ($p_c$) wie folgt definieren:

$ p_c = \displaystyle\frac{ q_c }{1- q_c }$

Bedingungen

Variablen

$q_c$

Eigene Porosität des Ton

$-$

$p_c$

Toneigener Volumenfaktor

$-$

Beziehung

ID:(15098, 0)

Gleichung

>Top, >Modell

Mit die Porosität ($f$) kann man der Die Strömung durch jede Schicht ($p_p$) wie folgt definieren:

$ p_p = \displaystyle\frac{ f }{1- f }$

Bedingungen

Variablen

$p_p$

Die Strömung durch jede Schicht

$-$

$f$

Porosität

$-$

Beziehung

ID:(2076, 0)

Gleichung

>Top, >Modell

Mithilfe von die Porosität ($f$), die Eigene Porosität des Sandes ($q_a$), die Eigene Porosität des Schlicks ($q_i$), die Eigene Porosität des Ton ($q_c$), die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$),

kann mit den Definitionen von der Die Strömung durch jede Schicht ($p_p$), der Eigener Volumenfaktor von Sand ($p_a$), der Schlammeigener Volumenfaktor ($p_i$) und der Toneigener Volumenfaktor ($p_c$) wie folgt umgeschrieben werden:

$ p_p = p_a g_a + p_i g_i + p_c g_c $

Bedingungen

Variablen

$p_p$

Die Strömung durch jede Schicht

$-$

$p_a$

Eigener Volumenfaktor von Sand

$-$

$g_a$

Massenanteil von Sand in der Probe

$-$

$g_i$

Massenanteil von Schluff in der Probe

$-$

$g_c$

Massenanteil von Ton in der Probe

$-$

$p_i$

Schlammeigener Volumenfaktor

$-$

$p_c$

Toneigener Volumenfaktor

$-$

Beziehung

Entwicklung

Mit den Variablen die Porosität ($f$), die Eigene Porosität des Sandes ($q_a$), die Eigene Porosität des Schlicks ($q_i$), die Eigene Porosität des Ton ($q_c$), die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$) haben wir folgende Beziehung:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Wenn wir die Beziehung für der Die Strömung durch jede Schicht ($p_p$) als:

$ p_p = \displaystyle\frac{ f }{1- f }$

Die Beziehung für der Eigener Volumenfaktor von Sand ($p_a$) als:

$ p_a = \displaystyle\frac{ q_a }{1- q_a }$

Die Beziehung für der Schlammeigener Volumenfaktor ($p_i$) als:

$ p_i = \displaystyle\frac{ q_i }{1- q_i }$

Und die Beziehung für der Toneigener Volumenfaktor ($p_c$) als:

$ p_c = \displaystyle\frac{ q_c }{1- q_c }$

Dann ergibt sich insgesamt:

$ p_p = p_a g_a + p_i g_i + p_c g_c $

ID:(1542, 0)