Storyboard

La microporosidad del suelo depende de su composición, por lo que es importante poder modelarla en función de la proporción de las diferentes componentes. Para ello, primero se estudia el factor volumétrico de las distintas texturas y luego se estima la porosidad, teniendo en cuenta que existe una componente básica proporcionada por la arcilla. A esto se suma la presencia de arena y limo, pero es importante tener en cuenta que la arcilla puede penetrar en los espacios entre los granos, lo que reduce la porosidad total.

>Modelo

ID:(2050, 0)

Concepto

>Top

ID:(15199, 0)

Concepto

>Top

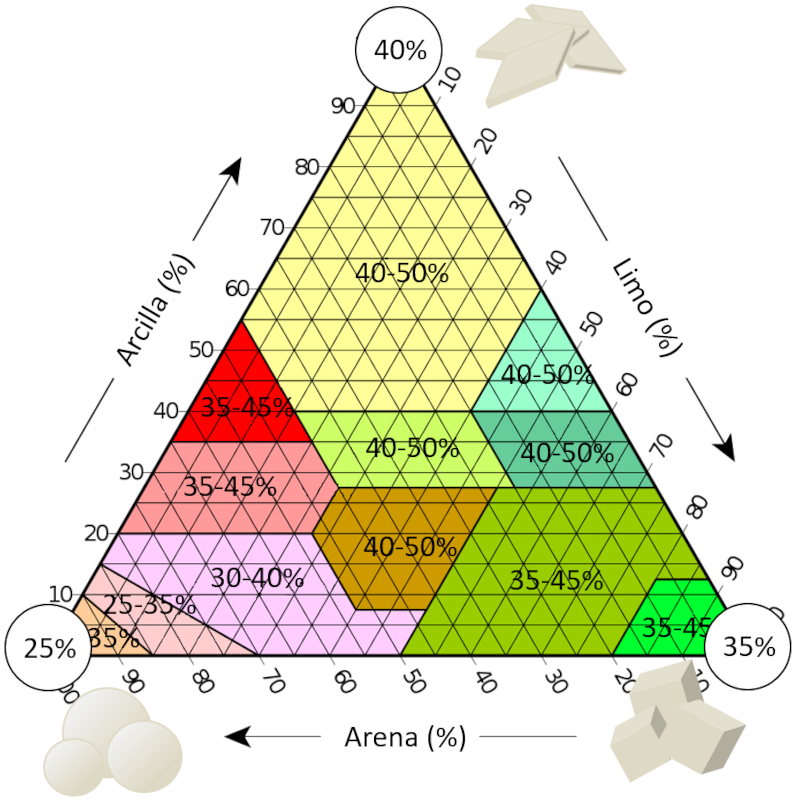
En el caso de los suelos en general, se puede estudiar el triángulo de texturas. Si se describe el rango típico de porosidad para cada tipo de suelo, se puede observar lo que se discutió anteriormente. En la esquina donde predomina la arena, se tiene una porosidad que puede llegar hasta el 25%, que es óptima para un modelo de esferas:

Triángulo de textura en que se incluye el rango de la porosidad obtenido de [1] y [2].

Ahora, si observamos la esquina del limo, notamos que se puede lograr una porosidad del 35%, lo que corresponde al nivel de espacio que no se puede llenar con cubos. Esto significa que el material no es capaz de ordenarse de manera que aproveche la estructura cúbica. Esto es probablemente una consecuencia de que a una escala de micrones ya existen fuerzas atractivas que generan un apilamiento desordenado.

En el último caso, podemos ver el límite de la arcilla, donde la porosidad alcanza un valor del orden del 40%, que nuevamente debe ser una consecuencia de la interacción entre las placas que pueden ordenar grupos de estas, pero no todo el sistema.

En resumen, se observa que en el extremo inferior izquierdo, donde el suelo está compuesto principalmente de arena, la porosidad puede llegar al 25%. Estos 25% representan precisamente la porosidad que se logra en el mejor caso para un modelo de esferas.

En otras palabras, existe una porosidad inherente a los tipos de suelo, y en aquellos en los que hay una presencia significativa de arcilla, esta última domina. El efecto de la arena y el limo solo prevalece en los casos extremos en los que el material tiene muy poca arcilla.

[1] Soil Mechanics and Foundations, Muni Budhu, (2011), John Wiley & Sons.

[2] Principles of Geotechnical Engineering, Braja M. Das, (2010), Cengage Learning

ID:(2078, 0)

Concepto

>Top

Si asumimos que las densidades de las diferentes componentes son similares:

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

los factores de volumen la fracción de volumen de arena en la muestra ($f_a$), la fracción de volumen del limo en la muestra ($f_i$), la fracción de volumen de arcilla en la muestra ($f_c$) en función de la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$) pueden expresarse de la siguiente manera:

$f_a = (1-f)\displaystyle\frac{\rho_s}{\rho_a}g_a \sim (1-f)g_a$

$f_i = (1-f)\displaystyle\frac{\rho_s}{\rho_i}g_i \sim (1-f)g_i$

$f_c = (1-f)\displaystyle\frac{\rho_s}{\rho_c}g_c \sim (1-f)g_c$

Esto nos permite estimar el rango de los factores volumétricos para los diferentes tipos de suelos, incluyendo la porosidad ($f$) y la fracción de volumen de macroporos en la muestra ($f_m$) nulos:

ID:(15096, 0)

Descripción

>Top

Dado que tenemos información para la temperatura en grados Celsius en estado 2 ($t_2$), el factor de volumen propio de la arena ($p_a$), el factor de volumen propio del limo ($p_i$), el factor de volumen propio de la arcilla ($p_c$), la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$) que satisface la ecuación:

y conocemos los valores medios para las diferentes texturas de suelo con los respectivos la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$), la fracción de masa de arcilla en la muestra ($g_c$) y el factor de volumen propio de la microporosidad ($p_p$) de:

Podemos realizar una regresión para determinar los valores de el factor de volumen propio de la microporosidad ($p_p$), el factor de volumen propio de la arena ($p_a$) y el factor de volumen propio del limo ($p_i$). El resultado es un ajuste con un R-cuadrado de 0.974 y los parámetros son los siguientes:

En general, el nivel de compactación de la arena con un la porosidad propia de la arena ($q_a$) del orden de 25% corresponde a una máxima compactación. Sin embargo, con un la porosidad propia del limo ($q_i$) del orden de 47%, es mayor que el óptimo, al igual que los 49% de la porosidad propia de la arcilla ($q_c$). En cualquier caso, los factores son una buena estimación debido al R cuadrado y los p-test de cada factor, que son significativamente menores que el límite tradicional de 0.05. Los intentos de considerar otras potencias en la regresión muestran que la aproximación lineal es la única que arroja coeficientes menores a 0.05, lo que sugiere que las muestras deben tener distribuciones que no presentan grandes efectos de mezcla y son simplemente sumas de componentes, como aglomeraciones.

ID:(15099, 0)

Concepto

>Top

Parámetro seleccionado

Cálculos

ID:(15218, 0)

Ecuación

>Top, >Modelo

De manera similar a cómo se definen las proporciones entre las masas de cada componente y la masa total, podemos establecer un sistema análogo utilizando los volúmenes. Con esto en mente, podemos definir la fracción de volumen de arena en la muestra ($f_a$) en relación con el volumen total ($V_t$). Esto nos permitirá calcular la cantidad de el volumen sólido de arena ($V_a$) en el contexto de el volumen total ($V_t$).

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

Condiciones

Variables

$f_a$

Fracción de volumen de arena en la muestra

$-$

$V_a$

Volumen sólido de arena

$m^3$

$V_t$

Volumen total

$m^3$

Relación

ID:(10369, 0)

Ecuación

>Top, >Modelo

De manera similar a cómo se definen las proporciones entre las masas de cada componente y la masa total, podemos establecer un sistema análogo utilizando los volúmenes. Con esto en mente, podemos definir la fracción de volumen del limo en la muestra ($f_i$) en relación con el volumen total ($V_t$). Esto nos permitirá calcular la cantidad de el volumen sólido de limo ($V_i$) en el contexto de el volumen total ($V_t$).

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

Condiciones

Variables

$f_i$

Fracción de volumen del limo en la muestra

$-$

$V_i$

Volumen sólido de limo

$m^3$

$V_t$

Volumen total

$m^3$

Relación

ID:(10367, 0)

Ecuación

>Top, >Modelo

Siguiendo un enfoque similar a la forma en que se definen las proporciones entre las masas de cada componente y la masa total, podemos establecer un sistema análogo utilizando los volúmenes. Con esto en mente, podemos definir la fracción de volumen de arcilla en la muestra ($f_c$) en relación con el volumen total ($V_t$). Esto nos permitirá calcular la cantidad de el volumen total ($V_t$) en el contexto del volumen total.

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

Condiciones

Variables

$f_c$

Fuerza por grano

$N$

$V_c$

Volumen sólido de arcilla

$m^3$

$V_t$

Volumen total

$m^3$

Relación

ID:(10368, 0)

Ecuación

>Top, >Modelo

De manera similar a cómo se definen las proporciones entre las masas de cada componente y la masa total, podemos establecer un sistema análogo utilizando los volúmenes. Con esto en mente, podemos definir la fracción de volumen de macroporos en la muestra ($f_m$) en relación con el volumen total ($V_t$). Esto nos permitirá calcular la cantidad de el volumen de los macroporos ($V_m$) en el contexto de el volumen total ($V_t$).

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

Condiciones

Variables

$f_m$

Fracción de volumen de macroporos en la muestra

$-$

$V_m$

Volumen de los macroporos

$m^3$

$V_t$

Volumen total

$m^3$

Relación

ID:(15084, 0)

Ecuación

>Top, >Modelo

La condición para suelos arcillosos en función de el volumen sólido de arena ($V_a$), el volumen sólido de limo ($V_i$), el volumen sólido de arcilla ($V_c$), el volumen de los macroporos ($V_m$), el volumen propio ($V_z$), la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$) y la porosidad propia de la arcilla ($q_c$) se expresa como:

Cuando utilizamos la ecuación del el volumen total ($V_t$) en función de el volumen propio ($V_z$) y la dividimos por el volumen total ($V_t$), podemos reescribirla en términos de la fracción de volumen de arena en la muestra ($f_a$), la fracción de volumen del limo en la muestra ($f_i$), la fracción de volumen de arcilla en la muestra ($f_c$), y la fracción de volumen de macroporos en la muestra ($f_m$) de la siguiente manera:

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

Condiciones

Variables

$f_c$

Fracción de volumen de arcilla en la muestra

$-$

$f_a$

Fracción de volumen de arena en la muestra

$-$

$f_m$

Fracción de volumen de macroporos en la muestra

$-$

$f_i$

Fracción de volumen del limo en la muestra

$-$

$q_c$

Porosidad propia de la arcilla

$-$

$q_a$

Porosidad propia de la arena

$-$

$q_i$

Porosidad propia del limo

$-$

Relación

Desarrollo

Con la ecuación del el volumen total ($V_t$) en función del el volumen propio ($V_z$) y de los el volumen de los macroporos ($V_m$):

$ V_t = V_m + V_z $

reemplazando el el volumen propio ($V_z$) en función del el volumen sólido de arena ($V_a$), el volumen sólido de limo ($V_i$), el volumen sólido de arcilla ($V_c$), el volumen de los macroporos ($V_m$), y la la porosidad propia de la arcilla ($q_c$) con:

$ V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$

obtenemos:

$V_t = V_a + V_i + \displaystyle\frac{1}{1-q_c}V_c+V_m$

Si dividimos esta ecuación por el el volumen total ($V_t$) y utilizamos las definiciones de la fracción de volumen de arena en la muestra ($f_a$)

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

para el la fracción de volumen del limo en la muestra ($f_i$)

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

para la la fracción de volumen de arcilla en la muestra ($f_c$)

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

y para los la fracción de volumen de macroporos en la muestra ($f_m$)

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

obtenemos la siguiente relación:

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

ID:(15086, 0)

Ecuación

>Top, >Modelo

El volumen de los poros ($V_p$) en un material arcilloso, que es una función del volumen de el volumen de los macroporos ($V_m$), la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$), la porosidad propia de la arcilla ($q_c$), el volumen sólido de arena ($V_a$), el volumen sólido de limo ($V_i$) y el volumen sólido de arcilla ($V_c$):

se puede reescribir dividiendo la ecuación por el volumen total ($V_t$) y expresando la ecuación en términos de la porosidad ($f$), la fracción de volumen de macroporos en la muestra ($f_m$), la fracción de volumen de arena en la muestra ($f_a$), la fracción de volumen del limo en la muestra ($f_i$) y la fracción de volumen de arcilla en la muestra ($f_c$), obteniendo así:

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

Condiciones

Variables

$f_c$

Fracción de volumen de arcilla en la muestra

$-$

$f_a$

Fracción de volumen de arena en la muestra

$-$

$f_i$

Fracción de volumen del limo en la muestra

$-$

$f$

Porosidad

$-$

$q_c$

Porosidad propia de la arcilla

$-$

$q_a$

Porosidad propia de la arena

$-$

$q_i$

Porosidad propia del limo

$-$

Relación

Desarrollo

El cálculo del el volumen de los poros ($V_p$) se puede realizar a partir de los el volumen de los macroporos ($V_m$), el volumen sólido de arcilla ($V_c$) y la porosidad propia de la arcilla ($q_c$) mediante la siguiente ecuación:

$ V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c $

Al dividir esta ecuación por el volumen total ($V_t$), podemos utilizar la porosidad ($f$)

$ f =\displaystyle\frac{ V_p }{ V_t }$

junto con la fracción de volumen de macroporos en la muestra ($f_m$)

$ f_m = \displaystyle\frac{ V_m }{ V_t }$

y la fracción de volumen de arcilla en la muestra ($f_c$)

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

lo que se simplifica a

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

ID:(2074, 0)

Ecuación

>Top, >Modelo

Como se definió La fracción de volumen de arena en la muestra ($f_a$) en función de el volumen sólido de arena ($V_a$) y el volumen total ($V_t$):

Por lo tanto, con la densidad de un grano de arena ($\rho_a$), la densidad solida ($\rho_s$), la porosidad ($f$) y la fracción de masa de arena en la muestra ($g_a$), puedes calcular el factor utilizando:

$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $

Condiciones

Variables

$\rho_a$

Densidad de un grano de arena

2.63e+3

$kg/m^3$

$\rho_s$

Densidad solida

$kg/m^3$

$g_a$

Fracción de masa de arena en la muestra

$-$

$f_a$

Fracción de volumen de arena en la muestra

$-$

$f$

Porosidad

$-$

Relación

Desarrollo

To calculate la fracción de volumen de arena en la muestra ($f_a$), you can use the definition with el volumen sólido de arena ($V_a$) and el volumen total ($V_t$) as follows:

$ f_a = \displaystyle\frac{ V_a }{ V_t }$

el volumen sólido de arena ($V_a$) can be expressed with la densidad de un grano de arena ($\rho_a$) and la masa seca de arena en la muestra ($M_a$) using the equation:

$ V_a =\displaystyle\frac{ M_a }{ \rho_a }$

For el volumen total ($V_t$), you can work with el volumen sólido ($V_s$) and el volumen de los poros ($V_p$) using the equation:

$ V_t = V_s + V_p $

using the expression for la porosidad ($f$):

$ f =\displaystyle\frac{ V_p }{ V_t }$

With these equations, we obtain the expression:

$V_t = \displaystyle\frac{1}{1-f} V_s$

Using the definition of la densidad solida ($\rho_s$) with la masa seca total de la muestra ($M_s$) and el volumen sólido ($V_s$):

$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$

we can express el volumen total ($V_t$) as:

$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$

This way, we obtain the expression for la fracción de volumen de arena en la muestra ($f_a$) as:

$f_a= \displaystyle\frac{V_a}{V_t}= \displaystyle\frac{M_a}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_a}$

which, with the equation for la fracción de masa de arena en la muestra ($g_a$):

$ g_a =\displaystyle\frac{ M_a }{ M_s }$

reduces to:

$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $

ID:(15093, 0)

Ecuación

>Top, >Modelo

Cómo se definió La fracción de volumen de arena en la muestra ($f_a$) en relación con el volumen sólido de limo ($V_i$) y el volumen total ($V_t$):

Por lo tanto, utilizando la densidad de un grano de limo ($\rho_i$), la densidad solida ($\rho_s$), la porosidad ($f$) y la fracción de masa de limo en la muestra ($g_i$), es posible calcular el factor con:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

Condiciones

Variables

$\rho_i$

Densidad de un grano de limo

2.65e+3

$kg/m^3$

$\rho_s$

Densidad solida

$kg/m^3$

$g_i$

Fracción de masa de limo en la muestra

$-$

$f_i$

Fracción de volumen del limo en la muestra

$-$

$f$

Porosidad

$-$

Relación

Desarrollo

Para calcular la fracción de volumen del limo en la muestra ($f_i$), puedes utilizar la definición con el volumen sólido de limo ($V_i$) y el volumen total ($V_t$) de la siguiente manera:

$ f_i = \displaystyle\frac{ V_i }{ V_t }$

el volumen sólido de limo ($V_i$) se puede expresar con la densidad de un grano de limo ($\rho_i$) y la masa seca de limo en la muestra ($M_i$) utilizando la ecuación:

$ V_i =\displaystyle\frac{ M_i }{ \rho_i }$

Para el volumen total ($V_t$), puedes trabajar con el volumen sólido ($V_s$) y el volumen de los poros ($V_p$) utilizando la ecuación:

$ V_t = V_s + V_p $

utilizando la expresión para la porosidad ($f$):

$ f =\displaystyle\frac{ V_p }{ V_t }$

Con estas ecuaciones, obtenemos la expresión:

$V_t = \displaystyle\frac{1}{1-f} V_s$

Utilizando la definición de la densidad solida ($\rho_s$) con la masa seca total de la muestra ($M_s$) y el volumen sólido ($V_s$):

$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$

podemos expresar el volumen total ($V_t$) de la siguiente manera:

$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$

De esta manera, obtenemos la expresión para la fracción de volumen del limo en la muestra ($f_i$) como:

$f_i= \displaystyle\frac{V_i}{V_t}= \displaystyle\frac{M_i}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_i}$

lo que, con la ecuación para la fracción de masa de limo en la muestra ($g_i$):

$ g_i =\displaystyle\frac{ M_i }{ M_s }$

se reduce a:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

ID:(15094, 0)

Ecuación

>Top, >Modelo

Cómo se definió La fracción de volumen de arena en la muestra ($f_a$) en relación a el volumen sólido de arcilla ($V_c$) y el volumen total ($V_t$):

Por lo tanto, utilizando la densidad de un grano de arcilla ($\rho_c$), la densidad solida ($\rho_s$), la porosidad ($f$) y la fracción de masa de arcilla en la muestra ($g_c$), se puede calcular el factor mediante:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

Condiciones

Variables

$\rho_c$

Densidad de un grano de arcilla

2.8e+3

$kg/m^3$

$\rho_s$

Densidad solida

$kg/m^3$

$g_c$

Fracción de masa de arcilla en la muestra

$-$

$f_c$

Fracción de volumen de arcilla en la muestra

$-$

$f$

Porosidad

$-$

Relación

Desarrollo

Para calcular la fracción de volumen de arcilla en la muestra ($f_c$), puedes utilizar la definición con el volumen sólido de arcilla ($V_c$) y el volumen total ($V_t$) de la siguiente manera:

$ f_c = \displaystyle\frac{ V_c }{ V_t }$

el volumen sólido de arcilla ($V_c$) se puede expresar con la densidad de un grano de arcilla ($\rho_c$) y la masa seca de arcilla en la muestra ($M_c$) utilizando la ecuación:

$ V_c =\displaystyle\frac{ M_c }{ \rho_c }$

Para el volumen total ($V_t$), puedes trabajar con el volumen sólido ($V_s$) y el volumen de los poros ($V_p$) utilizando la ecuación:

$ V_t = V_s + V_p $

utilizando la expresión para la porosidad ($f$):

$ f =\displaystyle\frac{ V_p }{ V_t }$

Con estas ecuaciones, obtenemos la expresión:

$V_t = \displaystyle\frac{1}{1-f} V_s$

Utilizando la definición de la densidad solida ($\rho_s$) con la masa seca total de la muestra ($M_s$) y el volumen sólido ($V_s$):

$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$

podemos expresar el volumen total ($V_t$) de la siguiente manera:

$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$

De esta manera, obtenemos la expresión para la fracción de volumen de arcilla en la muestra ($f_c$) como:

$f_i= \displaystyle\frac{V_c}{V_t}= \displaystyle\frac{M_c}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_c}$

lo que, con la ecuación para la fracción de masa de arcilla en la muestra ($g_c$):

$ g_c =\displaystyle\frac{ M_c }{ M_s }$

se reduce a:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

ID:(15095, 0)

Ecuación

>Top, >Modelo

La porosidad ($f$) es una función de la fracción de volumen de macroporos en la muestra ($f_m$), la fracción de volumen de arena en la muestra ($f_a$), la fracción de volumen del limo en la muestra ($f_i$), la fracción de volumen de arcilla en la muestra ($f_c$), la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$) y la porosidad propia de la arcilla ($q_c$):

Mediante las relaciones entre los factores volumétricos y los factores de masa la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$), en el caso en que no existan macroporos y se asuma que las densidades de las tres componentes son iguales, obtenemos:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Condiciones

Variables

$g_c$

Fracción de masa de arcilla en la muestra

$-$

$g_a$

Fracción de masa de arena en la muestra

$-$

$g_i$

Fracción de masa de limo en la muestra

$-$

$f$

Porosidad

$-$

$q_c$

Porosidad propia de la arcilla

$-$

$q_a$

Porosidad propia de la arena

$-$

$q_i$

Porosidad propia del limo

$-$

Relación

Desarrollo

La porosidad ($f$) es una función de el número de granos de limo en la muestra ($N_i$), la fracción de volumen de arena en la muestra ($f_a$), la fracción de volumen del limo en la muestra ($f_i$), la fracción de volumen de arcilla en la muestra ($f_c$), la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$) y la porosidad propia de la arcilla ($q_c$):

$ f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c $

Dado que con la densidad solida ($\rho_s$), la densidad de un grano de arena ($\rho_a$) y la fracción de masa de arena en la muestra ($g_a$) se tiene:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

y con la densidad de un grano de limo ($\rho_i$) y la fracción de masa de limo en la muestra ($g_i$) se tiene:

$ f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i $

además, con la densidad de un grano de arcilla ($\rho_c$) y la fracción de masa de arcilla en la muestra ($g_c$) se tiene:

$ f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c $

se puede, en el caso en que las densidades sean iguales:

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

y los macroporos no existan:

$f_m\sim 0$

obtener la siguiente relación:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

ID:(10370, 0)

Ecuación

>Top, >Modelo

Con la porosidad propia de la arena ($q_a$), se puede definir el factor de volumen propio de la arena ($p_a$) de la siguiente manera:

$ p_a = \displaystyle\frac{ q_a }{1- q_a }$

Condiciones

Variables

$p_a$

Factor de volumen propio de la arena

$-$

$q_a$

Porosidad propia de la arena

$-$

Relación

ID:(15087, 0)

Ecuación

>Top, >Modelo

Con la porosidad propia del limo ($q_i$), se puede definir el factor de volumen propio del limo ($p_i$) de la siguiente manera:

$ p_i = \displaystyle\frac{ q_i }{1- q_i }$

Condiciones

Variables

$p_i$

Factor de volumen propio del limo

$-$

$q_i$

Porosidad propia del limo

$-$

Relación

ID:(15088, 0)

Ecuación

>Top, >Modelo

Con la porosidad propia de la arcilla ($q_c$), se puede definir el factor de volumen propio de la arcilla ($p_c$) de la siguiente manera:

$ p_c = \displaystyle\frac{ q_c }{1- q_c }$

Condiciones

Variables

$p_c$

Factor de volumen propio de la arcilla

$-$

$q_c$

Porosidad propia de la arcilla

$-$

Relación

ID:(15098, 0)

Ecuación

>Top, >Modelo

Con la porosidad ($f$), se puede definir el factor de volumen propio de la microporosidad ($p_p$) de la siguiente manera:

$ p_p = \displaystyle\frac{ f }{1- f }$

Condiciones

Variables

$p_p$

Factor de volumen propio de la microporosidad

$-$

$f$

Porosidad

$-$

Relación

ID:(2076, 0)

Ecuación

>Top, >Modelo

Utilizando la porosidad ($f$), la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$), la porosidad propia de la arcilla ($q_c$), la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$),

puede ser reescrito con las definiciones de el factor de volumen propio de la microporosidad ($p_p$), el factor de volumen propio de la arena ($p_a$), el factor de volumen propio del limo ($p_i$) y el factor de volumen propio de la arcilla ($p_c$) de la siguiente manera:

$ p_p = p_a g_a + p_i g_i + p_c g_c $

Condiciones

Variables

$p_c$

Factor de volumen propio de la arcilla

$-$

$p_a$

Factor de volumen propio de la arena

$-$

$p_p$

Factor de volumen propio de la microporosidad

$-$

$p_i$

Factor de volumen propio del limo

$-$

$g_c$

Fracción de masa de arcilla en la muestra

$-$

$g_a$

Fracción de masa de arena en la muestra

$-$

$g_i$

Fracción de masa de limo en la muestra

$-$

Relación

Desarrollo

Con las variables la porosidad ($f$), la porosidad propia de la arena ($q_a$), la porosidad propia del limo ($q_i$), la porosidad propia de la arcilla ($q_c$), la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$), tenemos la siguiente relación:

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Si consideramos la relación para el factor de volumen propio de la microporosidad ($p_p$) como:

$ p_p = \displaystyle\frac{ f }{1- f }$

La relación para el factor de volumen propio de la arena ($p_a$) como:

$ p_a = \displaystyle\frac{ q_a }{1- q_a }$

La relación para el factor de volumen propio del limo ($p_i$) como:

$ p_i = \displaystyle\frac{ q_i }{1- q_i }$

Y la relación para el factor de volumen propio de la arcilla ($p_c$) como:

$ p_c = \displaystyle\frac{ q_c }{1- q_c }$

Entonces, el resultado general es:

$ p_p = p_a g_a + p_i g_i + p_c g_c $

ID:(1542, 0)