Porosité d'un sol spécifique
Storyboard 
La microporosité du sol dépend de sa composition, il est donc important de pouvoir la modéliser en fonction de la proportion des différentes composantes. Pour ce faire, on étudie d'abord le facteur volumétrique des différentes textures, puis on estime la porosité en tenant compte du fait qu'il existe une composante de base fournie par l'argile. De plus, la présence de sable et de limon est prise en compte, mais il est important de noter que l'argile peut pénétrer dans les espaces entre les grains, ce qui réduit la porosité totale.
ID:(2050, 0)
Porosité d'un sol spécifique
Storyboard 
La microporosité du sol dépend de sa composition, il est donc important de pouvoir la modéliser en fonction de la proportion des différentes composantes. Pour ce faire, on étudie d'abord le facteur volumétrique des différentes textures, puis on estime la porosité en tenant compte du fait qu'il existe une composante de base fournie par l'argile. De plus, la présence de sable et de limon est prise en compte, mais il est important de noter que l'argile peut pénétrer dans les espaces entre les grains, ce qui réduit la porosité totale.
Variables
Calculs
Calculs
Équations
Avec les variables a porosité ($f$), a porosité du sable ($q_a$), a porosité du limon ($q_i$), a porosité de l'argile ($q_c$), a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), nous avons la relation suivante :
Si nous consid rons la relation pour le calcul de l'équation de porosité ($p_p$) comme suit :
La relation pour le propre facteur de volume du sable ($p_a$) comme suit :
La relation pour le facteur de volume propre au slime ($p_i$) comme suit :
Et la relation pour le facteur de volume propre à l'argile ($p_c$) comme suit :
Alors le r sultat global est le suivant :
Le calcul de le volume poreux ($V_p$) peut tre effectu en utilisant les volumes de le volume des macropores ($V_m$), le volume solide d'argile ($V_c$) et a porosité de l'argile ($q_c$) avec l' quation suivante :
En divisant cette quation par le volume total ($V_t$), nous pouvons utiliser a porosité ($f$)
ainsi que a fraction volumique des macropores dans l'échantillon ($f_m$)
et a fraction volumique d'argile dans l'échantillon ($f_c$)
ce qui se simplifie en
A porosité ($f$) est une fonction de le nombre de grains de limon dans l'échantillon ($N_i$), a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$), a porosité du sable ($q_a$), a porosité du limon ($q_i$) et a porosité de l'argile ($q_c$) :
tant donn que avec a densité solide ($\rho_s$), a densité d'un grain de sable ($\rho_a$) et a fraction massique de sable dans l'échantillon ($g_a$) nous avons :
et avec a densité d'un grain de limon ($\rho_i$) et a fraction massique de limon dans l'échantillon ($g_i$) nous avons :
De plus, avec a longueur et largeur d'une plaque d'argile ($\rho_c$) et a fraction massique d'argile dans l'échantillon ($g_c$) nous avons :
il est possible, dans le cas o les densit s sont gales :
$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$
et qu'il n'y ait pas de macropores :
$f_m\sim 0$
d'obtenir la relation suivante :
Avec l' quation du le volume total ($V_t$) en fonction du le propre volume ($V_z$) et des le volume des macropores ($V_m$) :
en rempla ant le le propre volume ($V_z$) en fonction du le volume solide de sable ($V_a$), du le volume solide de limon ($V_i$), du le volume solide d'argile ($V_c$), du le volume des macropores ($V_m$) et du a porosité de l'argile ($q_c$) par :
nous obtenons :
$V_t = V_a + V_i + \displaystyle\frac{1}{1-q_c}V_c+V_m$
Si nous divisons cette quation par le volume total ($V_t$) et utilisons les d finitions de a fraction volumique de sable dans l'échantillon ($f_a$)
pour le a fraction volumique de limon dans l'échantillon ($f_i$)
pour le a fraction volumique d'argile dans l'échantillon ($f_c$)
et pour les a fraction volumique des macropores dans l'échantillon ($f_m$)
nous obtenons la relation suivante :
$ f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a $
f_a = rho_s *(1 - f )* g_a /( rho_a )
Pour calculer a fraction volumique de sable dans l'échantillon ($f_a$), vous pouvez utiliser la d finition avec le volume solide de sable ($V_a$) et le volume total ($V_t$) comme suit :
le volume solide de sable ($V_a$) peut tre exprim avec a densité d'un grain de sable ($\rho_a$) et a masse sèche de sable dans l'échantillon ($M_a$) en utilisant l' quation :
Pour le volume total ($V_t$), vous pouvez travailler avec le volume solide ($V_s$) et le volume poreux ($V_p$) en utilisant l' quation :
en utilisant l'expression pour a porosité ($f$) :
Avec ces deux quations, vous obtenez l'expression :
$V_t = \displaystyle\frac{1}{1-f} V_s$
En utilisant la d finition de a densité solide ($\rho_s$) avec a masse sèche totale de l'échantillon ($M_s$) et le volume solide ($V_s$) :
vous pouvez exprimer le volume total ($V_t$) comme suit :
$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$
De cette mani re, vous obtenez l'expression de a fraction volumique de sable dans l'échantillon ($f_a$) comme suit :
$f_a= \displaystyle\frac{V_a}{V_t}= \displaystyle\frac{M_a}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_a}$
ce qui, avec l' quation pour a fraction massique de sable dans l'échantillon ($g_a$) :
se r duit :
Exemples
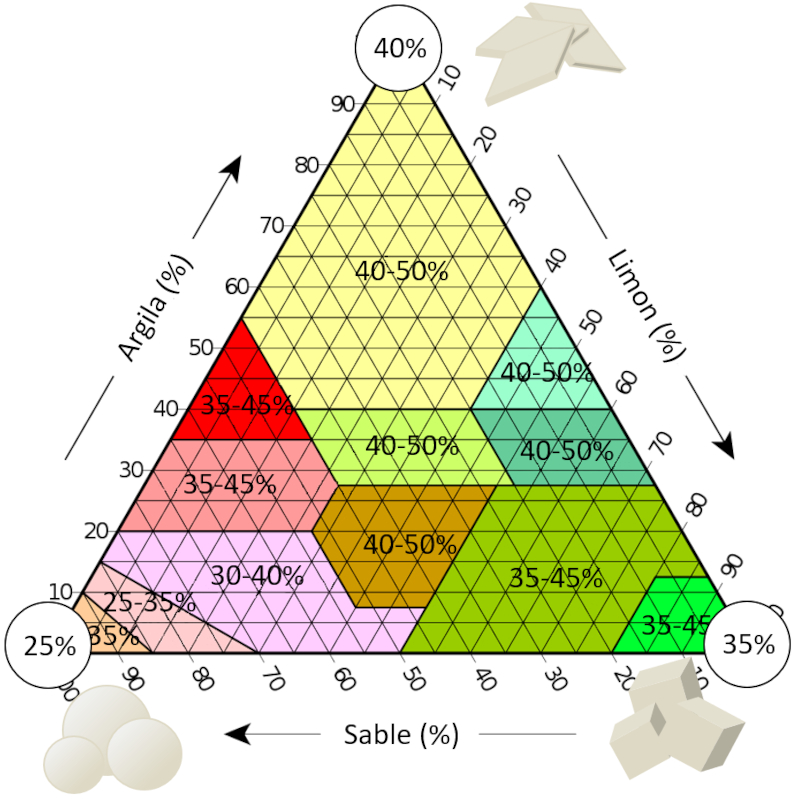
Dans le cas des sols en g n ral, nous pouvons tudier le triangle de texture du sol. Si nous d crivons la plage typique de porosit observ e pour chaque type de sol, nous pouvons voir ce qui a t discut pr c demment. Dans le coin o le sable pr domine, nous avons une porosit qui peut atteindre jusqu' 25 %, ce qui est optimal pour un mod le de sph res :
| Tapez | $g_a$ [%] | $g_i$ [%] | $g_c$ [%] | f [%] |
| Argile | 0-45 | 0-40 | 55-100 | 40-50 [1] |
| Limon | 23-52 | 28-50 | 8-27 | 40-50 [1] |
| Sable | 85-100 | 0-15 | 0-10 | 25-35 [1] |
| Silt | 0-20 | 80-100 | 0-13 | 35-45 [2] |
| Argile limoneuse | 0-20 | 40-60 | 40-60 | 40-50 [1] |
| Argile sableuse | 45-65 | 0-20 | 35-55 | 35-45 [1] |
| Argile limoneuse sableuse | 20-45 | 15-53 | 28-40 | 40-50 [1] |
| Argile limoneuse silteuse | 0-20 | 40-73 | 28-40 | 40-50 [1] |
| Argile sableuse silteuse | 45-80 | 0-33 | 20-35 | 35-45 [1] |
| Limoneux | 0-50 | 50-88 | 0-28 | 35-45 [2] |
| Sable limoneux | 43-85 | 0-50 | 0-20 | 30-40 [2] |
| Sable loameux | 70-90 | 0-30 | 0-15 | 25-35 [2] |
Maintenant, si nous examinons le coin du limon, nous pouvons voir qu'une porosit de 35 % peut tre atteinte, ce qui correspond au niveau d'espace qui ne peut pas tre rempli par des cubes. Cela signifie que le mat riau n'est pas capable de s'organiser de mani re exploiter la structure cubique. Cela est probablement une cons quence des forces attractives l' chelle des microns qui entra nent un empilement d sordonn .
Dans le dernier cas, nous pouvons voir la limite de l'argile, o la porosit atteint une valeur d'environ 40 %, ce qui doit nouveau tre une cons quence de l'interaction entre les plaques qui peuvent organiser des groupes d'entre elles, mais pas l'ensemble du syst me.
En r sum , nous observons qu'au coin inf rieur gauche, o le sol est principalement compos de sable, la porosit peut atteindre 25 %. Ces 25 % repr sentent pr cis ment la porosit atteinte dans le meilleur des cas pour un mod le de sph res.
En d'autres termes, il existe une porosit inh rente sp cifique aux types de sol, et dans les sols avec une pr sence significative d'argile, l'argile domine. L'effet du sable et du limon ne pr domine que dans les cas extr mes o le mat riau contient tr s peu d'argile.
[1] Soil Mechanics and Foundations, Muni Budhu, (2011), John Wiley & Sons.
[2] Principles of Geotechnical Engineering, Braja M. Das, (2010), Cengage Learning
Si l'on suppose que les densit s des diff rentes composantes sont similaires :
$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$
les facteurs de volume a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$) en fonction de a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), et a fraction massique d'argile dans l'échantillon ($g_c$) peuvent tre exprim s comme suit :
$f_a = (1-f)\displaystyle\frac{\rho_s}{\rho_a}g_a \sim (1-f)g_a$
$f_i = (1-f)\displaystyle\frac{\rho_s}{\rho_i}g_i \sim (1-f)g_i$
$f_c = (1-f)\displaystyle\frac{\rho_s}{\rho_c}g_c \sim (1-f)g_c$
Cela nous permet d'estimer la plage de facteurs volum triques pour diff rents types de sols, y compris lorsque a porosité ($f$) et a fraction volumique des macropores dans l'échantillon ($f_m$) sont nuls :
| Type | $f_a$ [%] | $f_i$ [%] | $f_c$ [%] | $f$ [%] |
| Argile | 0-25 | 0-22 | 30-55 | 40-50 |
| Limon | 13-29 | 15-28 | 4-15 | 40-50 |
| Sable | 60-70 | 0-11 | 0-7 | 25-35 |
| Silt | 0-11 | 44-55 | 0-7 | 35-45 |
| Argile limoneuse | 0-9 | 18-27 | 18-27 | 40-50 |
| Argile sableuse | 27-39 | 0-12 | 21-33 | 35-45 |
| Argile limoneuse sableuse | 11-25 | 8-29 | 15-22 | 40-50 |
| Argile limoneuse silteuse | 0-11 | 22-40 | 15-22 | 40-50 |
| Argile sableuse silteuse | 27-48 | 0-20 | 12-21 | 35-45 |
| Limoneux | 0-30 | 30-53 | 0-17 | 35-45 |
| Sable limoneux | 28-55 | 0-33 | 0-13 | 30-40 |
| Sable loameux | 49-63 | 0-21 | 0-11 | 25-35 |
tant donn les informations que nous avons pour le calcul de l'équation de porosité ($p_p$), le propre facteur de volume du sable ($p_a$), le facteur de volume propre au slime ($p_i$), le facteur de volume propre à l'argile ($p_c$), a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), qui satisfont l' quation :
et que nous connaissons les valeurs moyennes pour diff rentes textures de sol avec leurs a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), a fraction massique d'argile dans l'échantillon ($g_c$) et le calcul de l'équation de porosité ($p_p$) respectifs comme suit :
| Type | $g_a$ [-] | $g_i$ [-] | $g_c$ [-] | $p_p$ [-] |
| Argile | 0,225 | 0,200 | 0,775 | 0,818 |
| Loam | 0,375 | 0,390 | 0,175 | 0,818 |
| Sable | 0,925 | 0,075 | 0,050 | 0,429 |
| Silt | 0,100 | 0,900 | 0,065 | 0,818 |
| Argile limoneuse | 0,100 | 0,500 | 0,500 | 1,222 |
| Argile sableuse | 0,550 | 0,100 | 0,450 | 0,667 |
| Argile loameuse | 0,325 | 0,340 | 0,340 | 0,818 |
| Argile limono-sableuse | 0,100 | 0,565 | 0,340 | 0,818 |
| Argile sableuse loameuse | 0,625 | 0,165 | 0,275 | 0,667 |
| Silt loam | 0,250 | 0,690 | 0,140 | 0,667 |
| Sandy loam | 0,640 | 0,250 | 0,100 | 0,538 |
| Loamy sand | 0,800 | 0,150 | 0,075 | 0,429 |
Nous pouvons effectuer une r gression pour d terminer les valeurs de a température en degrés Celsius à l'état 2 ($t_2$), le propre facteur de volume du sable ($p_a$) et le facteur de volume propre au slime ($p_i$). Le r sultat est un ajustement avec un R carr de 0,974 et les param tres sont les suivants :
| Type | $p$ [%] | $q$ [%] | p-test |
| Sable (a) | 33,9 | 25,3 | 0,007029 |
| Silt (i) | 87,6 | 46,7 | 0,000041 |
| Argile (c) | 96,8 | 49,2 | 0,000158 |
En g n ral, le niveau de compactage du sable avec un a porosité du sable ($q_a$) d'environ 25 % correspond un compactage maximal. Cependant, avec un a porosité du limon ($q_i$) d'environ 47 %, il est sup rieur l'optimum, tout comme les 49 % pour a porosité de l'argile ($q_c$). Dans tous les cas, les facteurs sont une bonne estimation compte tenu du R carr lev et des faibles valeurs de p-test pour chaque facteur, qui sont significativement inf rieures au seuil traditionnel de 0,05. Les tentatives de prendre en compte d'autres puissances dans la r gression montrent que l'approximation lin aire est la seule qui produit des coefficients inf rieurs 0,05, ce qui sugg re que les chantillons doivent avoir des distributions qui ne pr sentent pas d'importants effets de m lange et sont simplement des sommes de composants, tels que des agr gats.
De mani re similaire la fa on dont les proportions entre les masses de chaque composant et la masse totale sont d finies, nous pouvons tablir un syst me analogue en utilisant les volumes. Avec cela l'esprit, nous pouvons d finir a fraction volumique de sable dans l'échantillon ($f_a$) par rapport le volume total ($V_t$). Cela nous permettra de calculer la quantit de le volume solide de sable ($V_a$) dans le contexte de le volume total ($V_t$).
De mani re similaire la fa on dont les proportions entre les masses de chaque composant et la masse totale sont d finies, nous pouvons tablir un syst me analogue en utilisant les volumes. Avec cela l'esprit, nous pouvons d finir a fraction volumique de limon dans l'échantillon ($f_i$) par rapport le volume total ($V_t$). Cela nous permettra de calculer la quantit de le volume solide de limon ($V_i$) dans le contexte de le volume total ($V_t$).
De mani re similaire la fa on dont les proportions entre les masses de chaque composant et la masse totale sont d finies, nous pouvons tablir un syst me analogue en utilisant les volumes. Avec cela l'esprit, nous pouvons d finir a fraction volumique d'argile dans l'échantillon ($f_c$) par rapport le volume total ($V_t$). Cela nous permettra de calculer la quantit de le volume total ($V_t$) dans le contexte du volume total.
De mani re similaire la fa on dont les proportions entre les masses de chaque composant et la masse totale sont d finies, nous pouvons tablir un syst me analogue en utilisant les volumes. Avec cela l'esprit, nous pouvons d finir a fraction volumique des macropores dans l'échantillon ($f_m$) par rapport le volume total ($V_t$). Cela nous permettra de calculer la quantit de le volume des macropores ($V_m$) dans le contexte de le volume total ($V_t$).
La condition pour les sols argileux en fonction de le volume solide de sable ($V_a$), le volume solide de limon ($V_i$), le volume solide d'argile ($V_c$), le volume des macropores ($V_m$), le propre volume ($V_z$) et a porosité de l'argile ($q_c$) est exprim e comme suit :
Lorsque nous utilisons l' quation pour le volume total ($V_t$) en fonction de le propre volume ($V_z$) et la divisons par le volume total ($V_t$), nous pouvons la r crire en fonction de a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$) et a fraction volumique des macropores dans l'échantillon ($f_m$) comme suit :
Le volume poreux ($V_p$) dans un mat riau argileux, qui est une fonction du volume des le volume des macropores ($V_m$), a porosité de l'argile ($q_c$) et le volume solide d'argile ($V_c$) :
peut tre r crite en divisant l' quation par le volume total ($V_t$) et en exprimant l' quation en termes de a porosité ($f$), a fraction volumique des macropores dans l'échantillon ($f_m$) et a fraction volumique d'argile dans l'échantillon ($f_c$), ce qui donne :
Comment a fraction volumique de sable dans l'échantillon ($f_a$) a t d fini en fonction de le volume solide de sable ($V_a$) et le volume total ($V_t$) :
Par cons quent, avec a densité d'un grain de sable ($\rho_a$), a densité solide ($\rho_s$), a porosité ($f$) et a fraction massique de sable dans l'échantillon ($g_a$) vous pouvez calculer le facteur l'aide de :
Comment a fraction volumique de sable dans l'échantillon ($f_a$) a t d fini en fonction de le volume solide de limon ($V_i$) et le volume total ($V_t$) :
Par cons quent, avec a densité d'un grain de limon ($\rho_i$), a densité solide ($\rho_s$), a porosité ($f$) et a fraction massique de limon dans l'échantillon ($g_i$) vous pouvez calculer le facteur en utilisant :
Comment a fraction volumique de sable dans l'échantillon ($f_a$) a t d fini en fonction de le volume solide d'argile ($V_c$) et le volume total ($V_t$) :
Par cons quent, avec a longueur et largeur d'une plaque d'argile ($\rho_c$), a densité solide ($\rho_s$), a porosité ($f$) et a fraction massique d'argile dans l'échantillon ($g_c$), vous pouvez calculer le facteur en utilisant :
A porosité ($f$) est une fonction de a fraction volumique des macropores dans l'échantillon ($f_m$), a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$), a porosité du sable ($q_a$), a porosité du limon ($q_i$) et a porosité de l'argile ($q_c$) :
En utilisant les relations entre les facteurs volum triques et les facteurs de masse a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), en supposant l'absence de macropores et des densit s gales pour les trois composantes, nous obtenons :
Avec a porosité du sable ($q_a$), on peut d finir le propre facteur de volume du sable ($p_a$) comme suit :
Avec a porosité du limon ($q_i$), vous pouvez d finir le facteur de volume propre au slime ($p_i$) comme suit :
Avec a porosité de l'argile ($q_c$), vous pouvez d finir le facteur de volume propre à l'argile ($p_c$) comme suit :
Avec a porosité ($f$), vous pouvez d finir le calcul de l'équation de porosité ($p_p$) comme suit :
En utilisant a porosité ($f$), a porosité du sable ($q_a$), a porosité du limon ($q_i$), a porosité de l'argile ($q_c$), a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$),
peut tre r crit avec les d finitions de le calcul de l'équation de porosité ($p_p$), le propre facteur de volume du sable ($p_a$), le facteur de volume propre au slime ($p_i$) et le facteur de volume propre à l'argile ($p_c$) comme suit :
ID:(2050, 0)