Benützer:
Anwendungen
Storyboard
Durch die Porosität des Bodens kann Regen- oder Bewässerungswasser in den Boden eindringen und die Napa erreichen. Daher müssen wir untersuchen, wie es basierend auf unserem geometrischen Modell modelliert werden kann, wenn sich das Wasser bewegt.
ID:(367, 0)
Strömungsdichte und hydraulische Leitfähigkeit
Konzept
Die Flussdichte ($j_s$) kann in Bezug auf die Hydraulische Leitfähigkeit ($K_s$) im infinitesimalen Grenzwert mit die Säulenhöhenunterschied ($dh$) und die Distanzdifferenz ($dx$) wie folgt ausgedrückt werden:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Dies bedeutet, dass je steiler der Gradient oder je steiler das Gelände ist, desto größer wird die Flussdichte ($j_s$) sein, wie im Diagramm dargestellt:
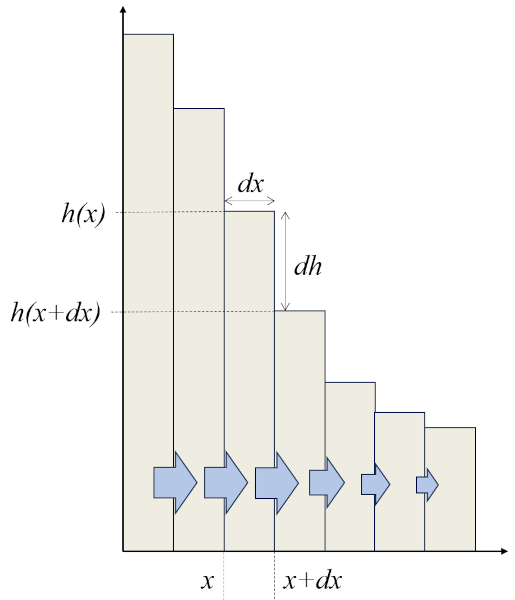
None
Das Diagramm zeigt, wie Balken mit gleichen Werten von Distanzdifferenz ($dx$) zunehmend kleinere Werte von Säulenhöhenunterschied ($dh$) haben, was zu einem abnehmenden Wert von Flussdichte ($j_s$) führt. Da das Volumen der Flüssigkeit erhalten bleibt, ist dies nur möglich, wenn ein anderer Fluss diese Reduzierung von Flussdichte ($j_s$) kompensiert. Dies könnte ein Fluss sein, der senkrecht zu dem im Diagramm gezeigten Fluss verläuft, zum Beispiel wenn die kürzeren Balken in einer Richtung senkrecht zum Diagramm breiter sind.
Dieses Problem führt zu Folgendem:
Die Höhe $h$ der Flüssigkeit kann nur als Ergebnis der Lösung einer Differentialgleichung berechnet werden, da sie die Anforderung erfüllen muss, dass das Volumen in dem gesamten Bereich, in dem der Fluss stattfindet, erhalten bleibt.
Darüber hinaus ist es wichtig zu beachten, dass:
Das negative Vorzeichen spiegelt die Tatsache wider, dass der Fluss immer von der höheren zur niedrigeren Höhenzone erfolgt. Wenn die Neigung negativ ist, führt das negative Vorzeichen zu einem positiven Fluss (von links nach rechts), und umgekehrt, wenn die Neigung positiv ist, ist der Fluss negativ (von rechts nach links).
ID:(930, 0)
Strömungsgleichung in einer Dimension
Konzept
Wenn wir den eindimensionalen Fall betrachten und den Prozess entlang der $x$-Achse beschreiben, können wir beobachten, wie sich die Höhe der Säule $\Delta h$ über ein Zeitintervall $\Delta t$ ändert. In diesem Fall ändert eine Säule mit der Breite $\Delta x$ ihr Volumen pro Einheit Länge im Laufe der Zeit um $\Delta x \Delta h/\Delta t$. Andererseits tritt die Menge an Flüssigkeit, die in der Säule bei $x$ eintritt, als $h(x) j_s(x)$ auf, während sie bei $x+\Delta x$ als $h(x+\Delta x) j_s(x+\Delta x)$ austritt:
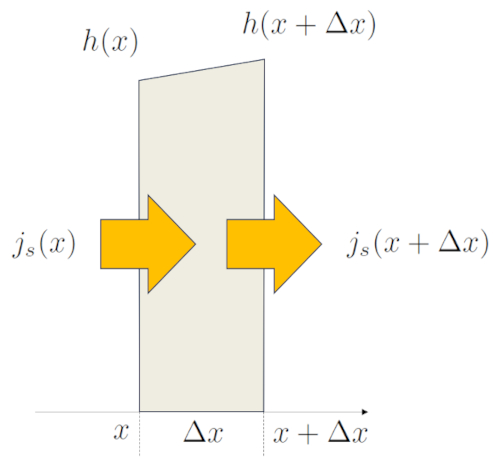
None
Daher entspricht die Änderung von die Höhe der Wassersäule am Boden ($h$) im Laufe der Zeit der Änderung des Produkts von die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) an der Position:
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
Partielle Ableitungen ähneln gewöhnlichen Ableitungen, mit dem Unterschied, dass sie auf Funktionen angewendet werden, die von mehr als einer Variablen abhängen. In solchen Fällen erinnert uns die partielle Ableitung, die durch das Symbol $\partial$ dargestellt wird, an die gewöhnliche Ableitung, die mit dem Buchstaben $d$ bezeichnet wird, mit dem Unterschied, dass die in den Nenner nicht erwähnten Variablen konstant gehalten werden.
ID:(2290, 0)
In einen Kanal fließen
Konzept
Im Fall des Flusses in Richtung eines Kanals kann das System eindimensional modelliert werden, wobei die Höhe der Wassersäule am Boden ($h$) eine Funktion von die Position der Wassersäule am Boden ($x$) ist, die die Flussdichte ($j_s$) repräsentiert und die Bedingung erfüllt
| $ h j_s = h_0 j_{s0} $ |
mit der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$), die das Profil des Wassers im Boden definieren:
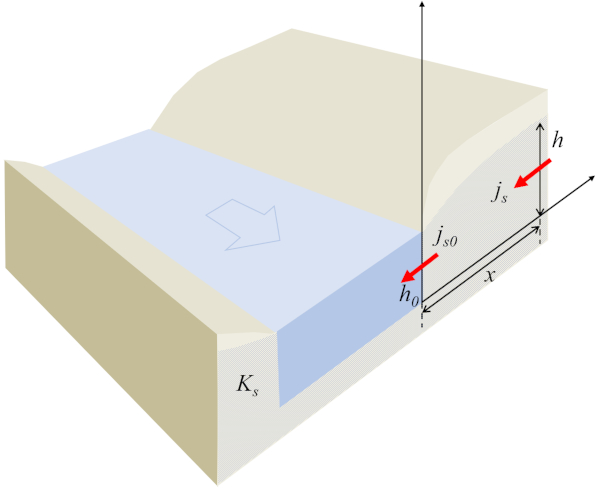
None
Der Schlüssel zu dieser Gleichung besteht darin, dass das Produkt aus die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) immer konstant sein muss. In diesem Sinne, wenn die Höhe der Wassersäule am Boden ($h$) steigt, sinkt die Flussdichte ($j_s$) und umgekehrt. Das Vorzeichen bleibt dabei immer gleich; daher wird der Fluss in Richtung des Kanals, d.h., der negative Fluss, nur auftreten, wenn der Grundwasserspiegel höher ist als der des Kanals. Wenn die Flüssigkeit dem Kanal näher kommt, sinkt der Grundwasserspiegel, was zu einer Zunahme der Flussdichte führt.
ID:(15104, 0)
Fließhöhenlösung in Richtung eines Kanals
Konzept
Die Lösung der eindimensionalen Strömungsgleichung in Richtung eines Kanals, bei der die Höhe der Wassersäule am Boden ($h$) als Funktion von die Referenzhöhe der Wassersäule ($h_0$) und die Position der Wassersäule am Boden ($x$) am Rand des Kanals zusammen mit der Charakteristische Länge der Strömung im Boden ($s_0$) berechnet wird, hat folgende Form:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $ |
Diese Lösung wird graphisch in Abhängigkeit von den zusätzlichen Faktoren $h/h_0$ und $x/s_0$ wie folgt dargestellt:
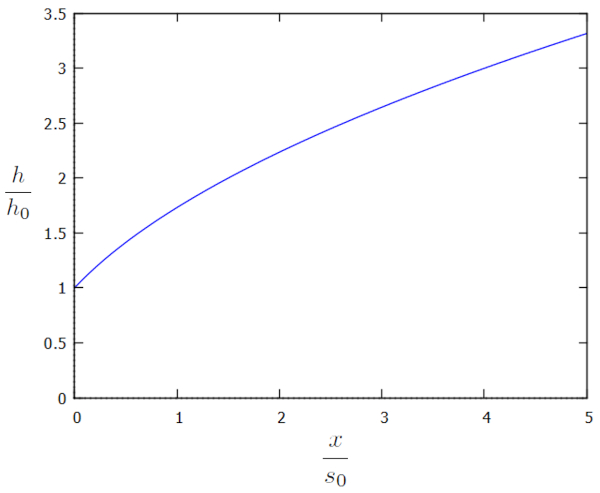
None
Das Profil zeigt, dass die Höhe der Wassersäule fernab des Kanals deutlich hoch ist. Aufgrund der Wasserentnahme durch den Kanal beginnt diese Höhe jedoch abzunehmen, bis sie den Rand des Kanals erreicht. Dynamisch bestimmt die Flussdichte ($j_s$) die Menge des in den Kanal fließenden Wassers, während sich die Referenzhöhe der Wassersäule ($h_0$) allmählich anpasst, bis es einen Gleichgewichtszustand erreicht. Mit anderen Worten, wenn der Wert von die Referenzhöhe der Wassersäule ($h_0$) im Verhältnis zur Gesamtmenge des ankommenden Wassers zu niedrig ist, erhöht er sich, und wenn er zu hoch ist, nimmt er ab. Auf diese Weise nimmt die Referenzhöhe der Wassersäule ($h_0$) den Wert an, der die Menge des eintreffenden Wassers mit der Menge des durch den Kanal fließenden Wassers ausgleicht.
ID:(15109, 0)
Flussdichtelösung in Richtung eines Kanals
Konzept
Die erhaltene Lösung für die Höhe und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) zeigt, dass die Flussdichte ($j_s$) wie folgt berechnet wird:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Wir können die Flussdichte ($j_s$) graphisch in Abhängigkeit von den zusätzlichen Faktoren $j_s/j_{s0}$ und $x/s_0$ wie folgt darstellen:
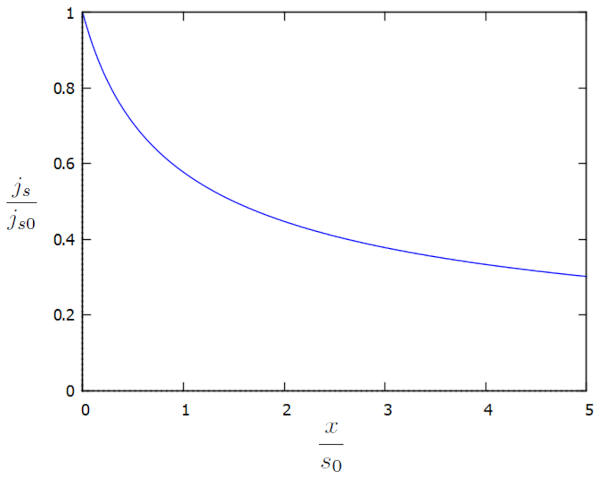
None
Es fällt auf, dass die Flussdichte ($j_s$) weiter zunimmt, je näher wir dem Kanal kommen, da die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist erforderlich, um die Fließgeschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ, um sie zu erhöhen.
ID:(15110, 0)
Fluss aus einem Kanal
Konzept
Im Fall, dass der Fluss aus dem Kanal aufsteigt, tritt die Situation auf, in der das Niveau von die Höhe der Wassersäule am Boden ($h$) abnehmen muss, wenn wir uns vom Kanal entfernen, um den Druckgradienten aufrechtzuerhalten, der den Fluss erzeugt. Das Problem ist, dass, wenn der Fluss sich schnell im Medium bewegt, die Höhe gegen null tendieren wird und folglich der Fluss gegen Unendlich streben wird, was keinen Sinn ergibt.
Das bedeutet, dass es in solch einer Situation keine stationäre Lösung gibt, und die einzige Lösung besteht darin, dass das Medium sich füllt, bis es die Höhe des Kanals erreicht und somit effektiv konstant wird.
Die Frage ist, ob es eine nicht-triviale stationäre Situation gibt, die eine reale und interessante Situation darstellt. Ein möglicher Fall ist, wenn das Niveau des Mediums so weit abnimmt, dass es niedriger wird als die Säule, bevor die Lösung divergiert. Dieser Fall entspricht der Situation, in der der Fluss an der Oberfläche auftritt und es keine Divergenz in der Lösung gibt. Dies würde bedeuten, dass ein Fluss erzeugt wird, der an einer bestimmten Stelle nach außen strömt, mit dem Risiko, das Fundament zu schwächen und damit das Medium zu destabilisieren, das als Damm fungiert.
ID:(4746, 0)
Situation, die Randbedingungen erfüllt
Konzept
Wenn wir eine Situation betrachten, in der der Fluss aus dem Kanal an die Oberfläche gelangen kann, haben wir eine Situation, in der der Fluss in das Medium eintritt und dann wieder austritt, was die Lösung möglich macht.
Das Auftreten an der Oberfläche bedeutet einfach, dass die Höhe der Flüssigkeitssäule höher wird als die des umgebenden Mediums. Tatsächlich würde dies, ähnlich wie im Fall des Flusses in Richtung eines Kanals, Wasser an der Oberfläche erzeugen, das, wenn es nicht abfließt, tatsächlich einen neuen Kanal bilden würde.
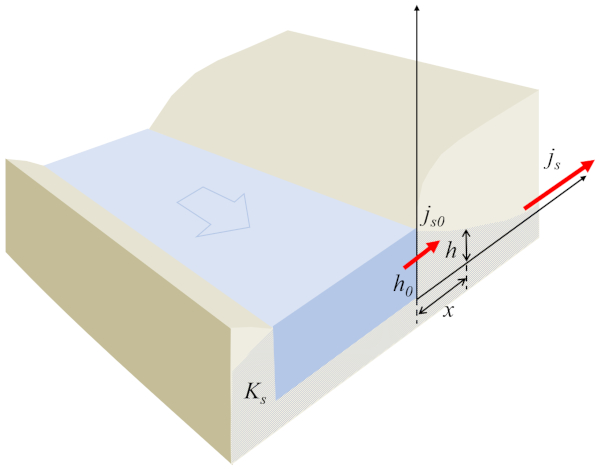
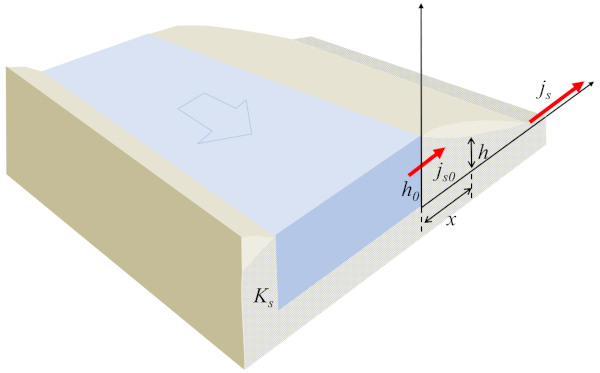
Im Fall des Flusses aus einem Kanal ist es möglich, das System eindimensional zu modellieren, wobei die Höhe der Wassersäule am Boden ($h$) eine Funktion von die Position der Wassersäule am Boden ($x$) ist, die die Flussdichte ($j_s$) darstellt und die folgende Bedingung erfüllt:
| $ h j_s = h_0 j_{s0} $ |
Mit der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$), die das Wasserprofil im Boden definieren, wie in der folgenden Abbildung gezeigt:
Der Schlüssel zur Gleichung liegt darin, dass das Produkt von die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) zu jeder Zeit konstant bleiben muss. In diesem Sinne, wenn die Höhe der Wassersäule am Boden ($h$) zunimmt, wird die Flussdichte ($j_s$) abnehmen, und umgekehrt. Darüber hinaus bleibt das Vorzeichen gleich. Daher wird der Fluss aus dem Kanal, d.h., der positive Fluss, nur auftreten, wenn die Höhe des Kanals größer ist als die des Punktes, an dem der Fluss entsteht. Wenn die Flüssigkeit sich vom Kanal entfernt, wird die Höhe abnehmen, und die Flussdichte wird zunehmen.
ID:(4370, 0)
Fließhöhenlösung aus einem Kanal
Konzept
Die Lösung der eindimensionalen Strömungsgleichung in einem Kanal, bei der der Wert von die Höhe der Wassersäule am Boden ($h$) in Abhängigkeit von die Referenzhöhe der Wassersäule ($h_0$) und die Position der Wassersäule am Boden ($x$) am Rand des Kanals zusammen mit der Charakteristische Länge der Strömung im Boden ($s_0$) berechnet wird, hat folgende Form:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }} $ |
Diese Lösung wird graphisch in Bezug auf die zusätzlichen Faktoren $h/h_0$ und $x/x_0$ wie folgt dargestellt:
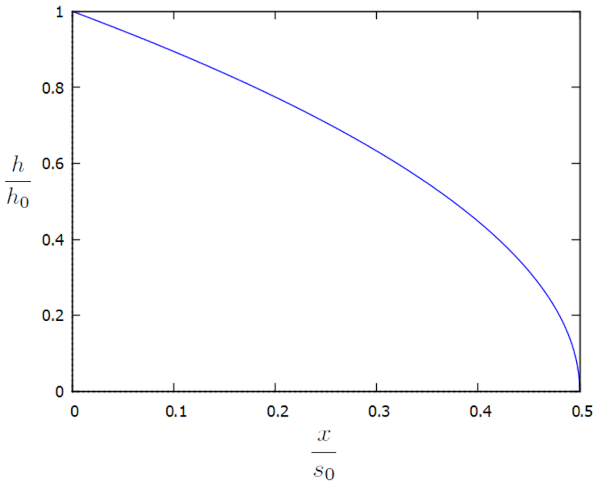
Das Profil zeigt, dass die Höhe abnimmt, wenn man sich vom Kanal entfernt, um einen Druckgradienten aufrechtzuerhalten. Es tritt jedoch ein Problem auf, wenn der Abstand die Hälfte von der Charakteristische Länge der Strömung im Boden ($s_0$) erreicht, da die Höhe der Säule auf null fällt und es keine Lösung für größere Entfernungen gibt (das Argument der Quadratwurzel wird negativ). Mit anderen Worten, damit die Lösung sinnvoll ist, muss ein Mechanismus vorhanden sein, der die Flüssigkeit entfernt, bevor diese kritische Entfernung erreicht wird.
ID:(4374, 0)
Flussdichtelösung aus einem Kanal
Konzept
Die erhaltene Lösung für die Höhe und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) zeigt uns, dass die Flussdichte ($j_s$) gleich ist:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }}} $ |
Wir können die Flussdichte ($j_s$) graphisch in Bezug auf die zusätzlichen Faktoren $j_s/j_{s0}$ und $x/x_0$ wie folgt darstellen:
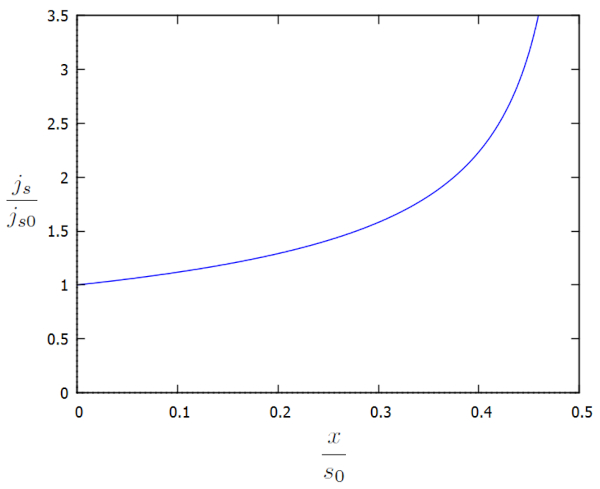
die Flussdichte ($j_s$) steigt weiter an, wenn wir uns dem Kanal nähern, da die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist notwendig, um die Fließgeschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ zu erhöhen.
ID:(7827, 0)
Damm I - Mina Córrego do Feijão
Konzept
Ein Beispiel, das den Effekt des Durchflusses durch die Basis im Fall eines Staudamms veranschaulicht, trat am Damm 1 der Mine 'Córrego do Feijão' in Brumadinho, Minas Gerais, Brasilien auf.
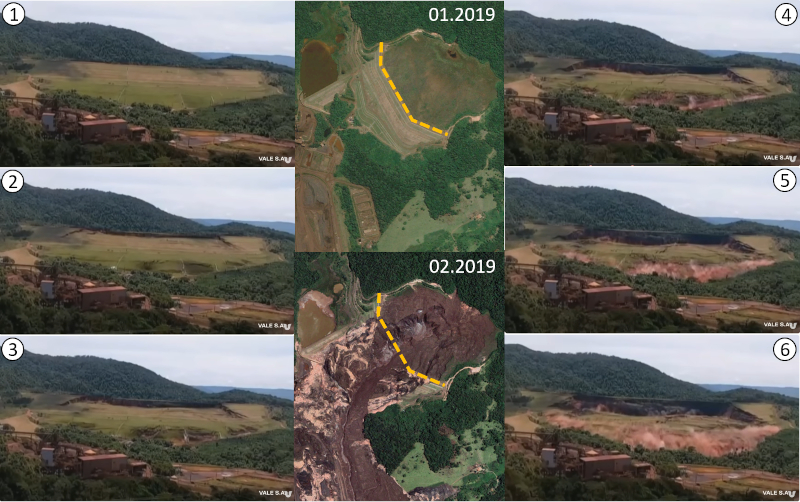
Am 25. Januar 2019 kollabierte Damm 1, der sich im Zentrum des Bildes befindet, wie in den Bildern 1 bis 6 dargestellt. Anfangs begann die Basis sich zu bewegen, während die Oberseite zu versinken begann. Schließlich trat ein Wasserstrom aus der Basis aus, als die gesamte Struktur zusammenbrach. Auf dem unteren zentralen Bild sehen Sie die Situation, nachdem der Damm sich vollständig auf der Seite entleert hatte, die ihn enthielt ([1], [2]):
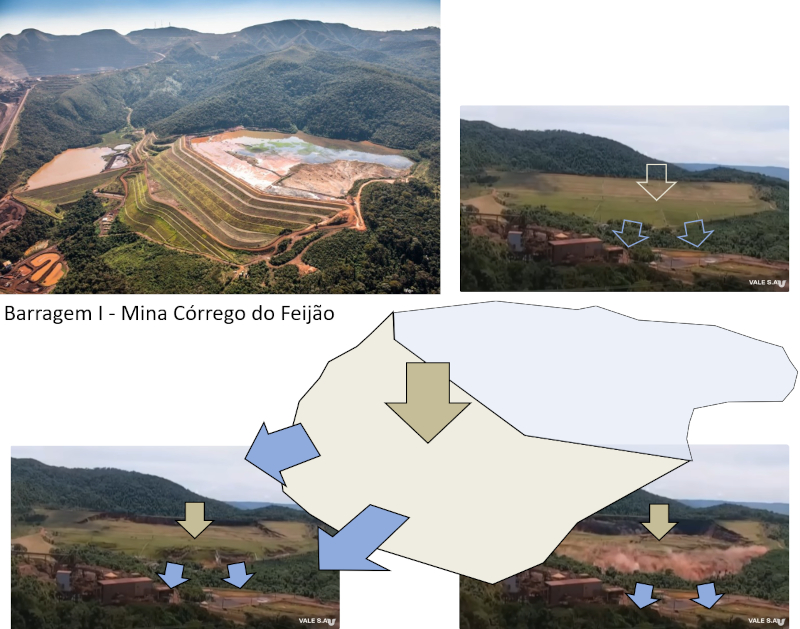
Das Bild oben links zeigt den Damm vor dem Zusammenbruch, und das Diagramm erklärt, wie das Wasser gegen die Basisfläche drückt (blaue Pfeile) und das Zentrum kollabiert (beiger Pfeil). Die Bilder zeigen die Struktur erneut vor dem Zusammenbruch (Foto oben rechts), als die Basis gezwungen wird, was dazu führt, dass der obere Teil zusammenbricht (Foto unten links), und den resultierenden Wasserfluss an der Basis (Foto unten rechts) [3]:
Die Dynamik wird durch den hohen Druck und den hohen Fluss an der Basis getrieben, was das Auftreten von Wasser durch diesen Weg erklärt.
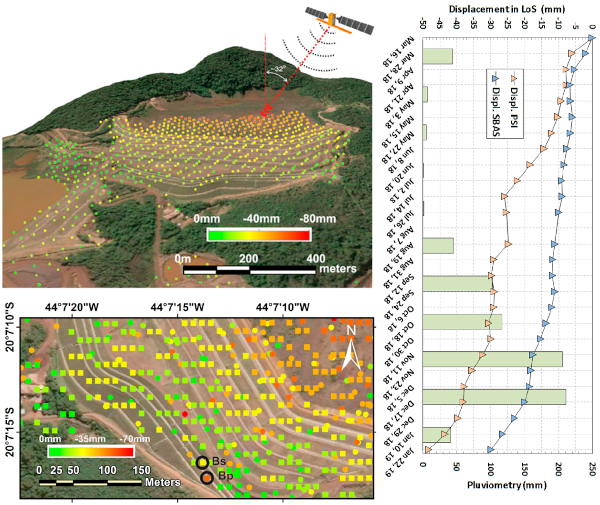
In diesem Fall gab es mehrere Anzeichen von Gefahr, was zu einer detaillierten Satellitenüberwachung der Bewegung mehrerer Punkte über einen Zeitraum von mehr als einem Jahr führte. Die Punkte sind in der oberen Abbildung markiert, und auf der linken unteren Abbildung sehen Sie eine Detailansicht der Basis. Insbesondere werden die Punkte hervorgehoben, die die größte Gesamtverschiebung erfuhren (Bs und Bp), die auch im Diagramm rechts dargestellt sind. Das Diagramm zeigt auch die Niederschlagsmenge, die in gewissem Maße beiträgt, aber nicht unbedingt ein Schlüsselfaktor ist [4]:
Dieses Beispiel soll zeigen, wie hoher Druck an der Basis in Verbindung mit einem hohen Wasserfluss zur beobachteten Dynamik beiträgt, ohne notwendigerweise zu erklären, wann oder wie sie instabil wurde. Dies wird weiter erforscht.
[1] Google Earth Pro für Brumadinho, Minas Gerais, Brasilien, Januar 2019 und Februar 2019
[2] Kameras der Vale S.A.
[3] Strafrechtliche Untersuchungsverfahren Nr. MPMG-0090.19.000013-4, Polizeiuntersuchung Nr. PCMG-7977979, MINISTÉRIO PÚBLICO DO ESTADO DE MINAS GERAIS
[4] Verformungen vor dem Brumadinho-Dammbruch, aufgedeckt durch Sentinel-1-InSAR-Daten unter Verwendung von SBAS- und PSI-Techniken, Fábio F. Gama, José C. Mura, Waldir R. Paradella und Cleber G. de Oliveira, MDPI, Remote Sens. 2020, 12, 3664.
ID:(4378, 0)
In einen Brunnen fließen
Konzept
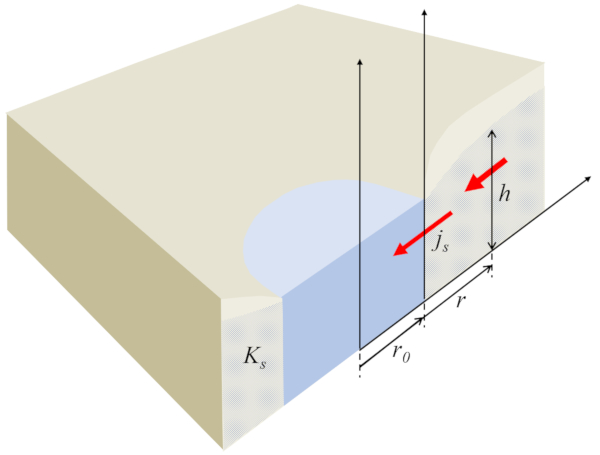
Im Fall des Grundwasserflusses zu einem Brunnen wird die Höhe der Wassersäule am Boden ($h$) als Funktion von der Radius von der Mitte des Bohrlochs ($r$) mit der Brunnenradius ($r_0$), der Charakteristische Länge der Strömung im Boden ($s_0$) und die Referenzhöhe der Wassersäule ($h_0$) durch
| $ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $ |
repräsentiert, was das Wasserprofil im Boden definiert:
ID:(4371, 0)
Fließhöhenlösung in Richtung eines Brunnens
Konzept
Die Lösung der eindimensionalen Fließgleichung zu einem Brunnen, bei der der Wert von die Höhe der Wassersäule am Boden ($h$) als Funktion von der Radius von der Mitte des Bohrlochs ($r$), die Referenzhöhe der Wassersäule ($h_0$) und der Brunnenradius ($r_0$) am Rand des Brunnens zusammen mit der Charakteristische Länge der Strömung im Boden ($s_0$) berechnet wird, hat folgende Form:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
Diese Lösung wird graphisch in Bezug auf die zusätzlichen Faktoren $h/h_0$ und $r/r_0$ für verschiedene $r_0/s_0$ wie folgt dargestellt:
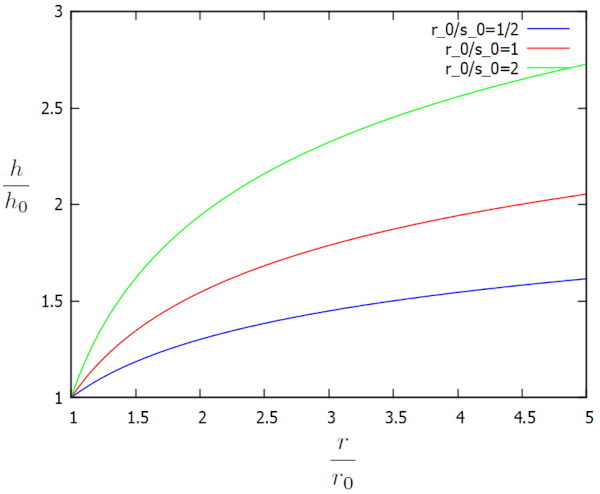
Das Profil zeigt, dass die Höhe der Wassersäule weit entfernt vom Brunnen deutlich hoch ist. Aufgrund der Wasserentnahme durch den Brunnen beginnt diese Höhe jedoch abzunehmen, bis sie den Rand des Brunnens erreicht. Dynamisch bestimmt die Flussdichte ($j_s$) die Menge des zum Brunnen fließenden Wassers, während die Referenzhöhe der Wassersäule ($h_0$) sich allmählich anpasst, um einen Gleichgewichtszustand zu erreichen. Mit anderen Worten, wenn der Wert von die Referenzhöhe der Wassersäule ($h_0$) im Verhältnis zur Gesamtmenge des zum Brunnen gelangenden Wassers zu niedrig ist, erhöht er sich, und wenn er zu hoch ist, verringert er sich. Auf diese Weise nimmt die Referenzhöhe der Wassersäule ($h_0$) den Wert an, der die Menge des ankommenden Wassers mit der Menge des durch den Brunnen abgepumpten Wassers ausgleicht.
ID:(10591, 0)
Flussdichtelösung in Richtung eines Brunnens
Konzept
Die erhaltene Lösung für die Höhe und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und der Radius von der Mitte des Bohrlochs ($r$), der Brunnenradius ($r_0$), der Charakteristische Länge der Strömung im Boden ($s_0$) zeigt uns, dass die Flussdichte ($j_s$) gleich ist:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
Diese Lösung wird graphisch in Bezug auf die zusätzlichen Faktoren $j_s/j_{s0}$ und $r/r_0$ für verschiedene Werte von $r_0/s_0$ wie folgt dargestellt:
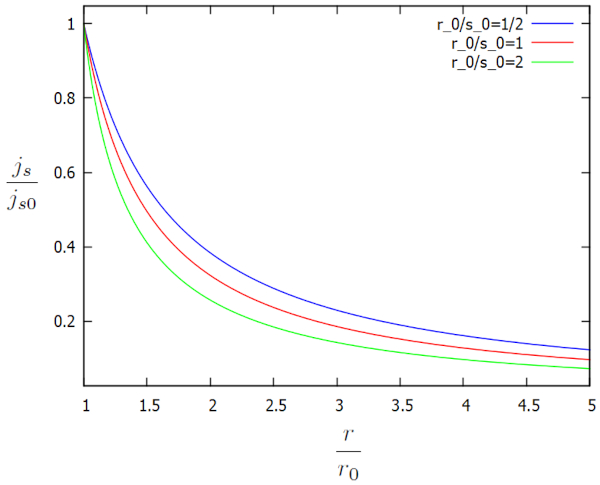
None
die Flussdichte ($j_s$) steigt weiter an, wenn wir uns dem Kanal nähern, während die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist notwendig, um die Fließgeschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ, um sie zu erhöhen.
ID:(2209, 0)
Modell
Konzept
Variablen
Parameter
Ausgewählter Parameter
Berechnungen
Gleichung
$ \vec{j}_s = - K_s \nabla h $
&j_s = - K_s * @GRAD( h , x )
$ h \nabla^2 h + \nabla h \cdot \nabla h = 0 $
h * &D^2 h + &D h * &D h = 0
$ h \displaystyle\frac{ dh }{ dx } = -\displaystyle\frac{ h_0 ^2 }{ x_0 } $
h * @DIFF( h , x, 1) = - h_0 ^2/ x_0
$ h \displaystyle\frac{ dh }{ dx } = \displaystyle\frac{ h_0 ^2 }{ s_0 } $
h * @DIFF( h , x, 1) = h_0 ^2/ s_0
$ h j_s = h_0 j_{s0} $
h * j_s = h_0 * j_{s0}
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $
h / h_0 = sqrt(1 + 2* r_0 *log( r / r_0 )/ s_0 )
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $
h / h_0 = sqrt(1 + 2* x / s_0 )
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }} $
h / h_0 = sqrt(1 - 2* x / x_0 )
$ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }}} $
j / j_s0 = 1/sqrt(1 + 2* x / s_0 )
$ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }}} $
j / j_s0 = 1/sqrt(1 - 2* x / x_0 )
$ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$
j = j_s0 /(( r / r_0 )*sqrt(1 + 2* r_0 *log( r / r_0 )/ s_0 ))
$ j_s = -\displaystyle\frac{ k_s }{ \eta }\displaystyle\frac{ dp }{ dx }$
j_s = - k_s * dp /( eta * dx )
$ k_s = \displaystyle\frac{ \eta }{ \rho_w g } K_s $
k_s = eta * K_s /( rho_w * g )
$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$
K_s = r_0 ^2 * f ^3 * rho_w * g /(8* q_0 *(1- f )^2* eta )
$ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$
k_s = r_0 ^2 * f ^3/(8* q_0 *(1 - f )^2)
$ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $
r * @DIFF( h ^2, r, 1) = h_0 ^2* r_0 / s_0
$ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$
s_0 = abs( j_s0 )/( K_s * h_0 )
$\displaystyle\frac{\partial h}{\partial t} = - \vec{\nabla} \cdot ( h \vec{j}_s )$
D_t h = - &D * (h &j_s)
ID:(15224, 0)
Hydraulische Leitfähigkeit des Bodens
Gleichung
Der Fluss von Flüssigkeit in einem porösen Medium wie Boden wird mithilfe der Variable die Flussdichte ($j_s$) gemessen, die die Durchschnittsgeschwindigkeit repräsentiert, mit der sich die Flüssigkeit durch das Medium bewegt. Bei der Modellierung des Bodens und wie die Flüssigkeit durch ihn hindurchfließt, stellt sich heraus, dass dieser Prozess von Faktoren wie die Porosität ($f$) und der Radius einer generischen Korns ($r_0$) beeinflusst wird, die, wenn sie größer sind, den Fluss erleichtern, während die Viskosität ($\eta$) den Durchgang durch Kapillaren behindert und die Fließgeschwindigkeit reduziert.
Das Modell integriert schließlich, was wir als die Hydraulische Leitfähigkeit ($K_s$) bezeichnen werden, eine Variable, die von den Wechselwirkungen zwischen der Radius einer generischen Korns ($r_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$) und die Generische eigene Porosität ($q_0$) abhängt:
 $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
Da die Flussdichte ($j_s$) durch die Gleichung:
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
mit der Radius einer generischen Korns ($r_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$), die Generische eigene Porosität ($q_0$), die Höhendifferenz ($\Delta h$) und der Probenlänge ($\Delta L$) in Beziehung steht, können wir einen Faktor definieren, den wir die Hydraulische Leitfähigkeit ($K_s$) nennen, wie folgt:
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
Dieser Faktor umfasst alle Elemente, die mit den Eigenschaften des Bodens und der Flüssigkeit, die durch ihn fließt, zusammenhängen.
die Hydraulische Leitfähigkeit ($K_s$) drückt aus, wie leicht die Flüssigkeit durch das poröse Medium geleitet wird. Tatsächlich erhöht sich die Hydraulische Leitfähigkeit ($K_s$) mit die Porosität ($f$) und der Radius einer generischen Korns ($r_0$) und verringert sich mit die Generische eigene Porosität ($q_0$) und die Viskosität ($\eta$).
ID:(4739, 0)
Bodendurchlässigkeit
Gleichung
Die Hydraulische Leitfähigkeit ($K_s$) repräsentiert, wie sich die Flüssigkeit im Medium verhält. Ein Teil von die Hydraulische Leitfähigkeit ($K_s$) ist inhärent den Eigenschaften des Mediums selbst, während ein anderer Teil Konstanten enthält, die das Verhalten der Flüssigkeit beschreiben. Daher macht es Sinn, eine neue Konstante einzuführen, die spezifisch für das Medium ist und nicht für die fließende Flüssigkeit.
Daher steht die Hydraulische Leitfähigkeit ($k_s$) in Beziehung zu der Radius einer generischen Korns ($r_0$), die Porosität ($f$) und die Generische eigene Porosität ($q_0$) durch folgende Definition:
| $ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$ |
Da die Hydraulische Leitfähigkeit ($K_s$) durch die Gleichung:
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
mit der Radius einer generischen Korns ($r_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$) und die Generische eigene Porosität ($q_0$) verknüpft ist, können wir den Teil, der ausschließlich vom Boden abhängt, als die Hydraulische Leitfähigkeit ($k_s$) definieren und wie folgt ausdrücken:
| $ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$ |
ID:(10595, 0)
Permeabilität und hydraulische Leitfähigkeit
Gleichung
Die Hydraulische Leitfähigkeit ($k_s$) kann aus die Hydraulische Leitfähigkeit ($K_s$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$) und die Viskosität ($\eta$) mithilfe des folgenden Ausdrucks berechnet werden:
| $ k_s = \displaystyle\frac{ \eta }{ \rho_w g } K_s $ |
Die Hydraulische Leitfähigkeit ($k_s$) in Bezug auf der Radius einer generischen Korns ($r_0$), die Porosität ($f$) und die Generische eigene Porosität ($q_0$) steht, ist es gleich
| $ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$ |
Daher ergibt sich mit der Gleichung für die Hydraulische Leitfähigkeit ($K_s$), zusammen mit die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$) und die Viskosität ($\eta$),
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
die Beziehung zwischen die Hydraulische Leitfähigkeit ($k_s$) und die Hydraulische Leitfähigkeit ($K_s$) als
| $ k_s = \displaystyle\frac{ \eta }{ \rho_w g } K_s $ |
In der Regel werden Bodencharakterisierungsmessungen mit einer bestimmten Flüssigkeit durchgeführt, was zu einem spezifischen Wert von eine Hydraulische Leitfähigkeit ($K_s$) führt. Mit diesem Wert kann dann die Hydraulische Leitfähigkeit ($k_s$) mithilfe der oben genannten Gleichung berechnet werden.
ID:(34, 0)
Strömungsdichte und Druckgradient
Gleichung
Die Flussdichte ($j_s$) kann in Abhängigkeit von die Höhe der Wassersäule am Boden ($h$) oder basierend auf die Druck der Wassersäule ($p_t$), das von der Flüssigkeitssäule erzeugt wird, ausgedrückt werden. Wenn wir die Definition von die Hydraulische Leitfähigkeit ($k_s$) in Bezug auf die Hydraulische Leitfähigkeit ($K_s$) verwenden, erhalten wir die folgende Ausdrucksformel für die Viskosität ($\eta$) und die Position der Wassersäule am Boden ($x$):
| $ j_s = -\displaystyle\frac{ k_s }{ \eta }\displaystyle\frac{ dp }{ dx }$ |
Die Druckunterschied ($\Delta p$) in Bezug auf die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$) und die Höhendifferenz ($\Delta h$) wird gemäß folgender Gleichung berechnet:
| $ \Delta p = \rho_w g \Delta h $ |
im infinitesimalen Grenzwert, in dem die Druckunterschied ($\Delta p$) gleich die Druckdifferenzial ($dp$) ist, gekennzeichnet als:
$\Delta p \rightarrow dp$
und in dem die Höhendifferenz ($\Delta h$) gleich die Säulenhöhenunterschied ($dh$) ist, gekennzeichnet als:
$\Delta h \rightarrow dh$
Unter Verwendung der Beziehung von die Flussdichte ($j_s$) zu die Hydraulische Leitfähigkeit ($K_s$), die Säulenhöhenunterschied ($dh$) und die Distanzdifferenz ($dx$), die wie folgt ausgedrückt wird:
| $$ |
und der Beziehung für die Hydraulische Leitfähigkeit ($k_s$) zu die Viskosität ($\eta$), die wie folgt ausgedrückt wird:
| $ k_s = \displaystyle\frac{ \eta }{ \rho_w g } K_s $ |
können wir die folgende Gleichung ableiten:
| $ j_s = -\displaystyle\frac{ k_s }{ \eta }\displaystyle\frac{ dp }{ dx }$ |
ID:(45, 0)
Strömungsdichte und Höhengradient in mehr Dimensionen
Gleichung
Angesichts der Tatsache, dass die eindimensionale Gleichung für die Flussdichte ($j_s$) wie folgt ausgedrückt wird: die Hydraulische Leitfähigkeit ($K_s$), die Höhe der Wassersäule am Boden ($h$) und die Position der Wassersäule am Boden ($x$):
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Ist es möglich, diese Gleichung für den Fall eines homogenen Mediums zu verallgemeinern, wodurch sich eine Gleichung für die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$) ergibt, bei der die Hydraulische Leitfähigkeit ($K_s$) konstant bleibt, wie folgt:
| $ \vec{j}_s = - K_s \nabla h $ |
ID:(999, 0)
Strömungsgleichung in mehr als einer Dimension
Gleichung
Wenn wir die Gleichung in einer Dimension für die Höhe der Wassersäule am Boden ($h$) als Funktion von der Zeit ($t$) und die Position der Wassersäule am Boden ($x$) mit die Flussdichte ($j_s$) verallgemeinern:
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
und die partielle Ableitung durch eine Divergenz ersetzen, erhalten wir mit die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$):
| $\displaystyle\frac{\partial h}{\partial t} = - \vec{\nabla} \cdot ( h \vec{j}_s )$ |
ID:(15111, 0)
Statische Lösung in einer Dimension
Gleichung
Im Fall der eindimensionalen Höhengleichung, ausgedrückt als:
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
können wir den stationären Fall untersuchen, was bedeutet, dass die Höhe der Wassersäule am Boden ($h$) durch die Flussdichte ($j_s$) konstant sein muss und insbesondere Werte an einem bestimmten Punkt annehmen kann, der durch die Referenzhöhe der Wassersäule ($h_0$) und der Strömung an einem Referenzpunkt ($j_{s0}$) dargestellt wird:
| $ h j_s = h_0 j_{s0} $ |
Wenn für die Höhe der Wassersäule am Boden ($h$) geteilt durch die Flussdichte ($j_s$) die Gleichung
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
im stationären Fall auf
$\displaystyle\frac{d}{dx} (h j_s) = 0$
reduziert wird, was dem konstanten Produkt von die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) entspricht. Wenn Sie Werte für einen bestimmten Punkt haben, der durch die Referenzhöhe der Wassersäule ($h_0$) und der Strömung an einem Referenzpunkt ($j_{s0}$) definiert ist, dann haben Sie:
| $ h j_s = h_0 j_{s0} $ |
Hinweis: Die Differentialgleichung ist eine gewöhnliche Differentialgleichung, da sie ausschließlich von der Position $x$ abhängt und nicht mehr von der Zeit $t$.
ID:(15107, 0)
Charakteristische Länge der Strömung im Boden
Gleichung
Mit die Hydraulische Leitfähigkeit ($K_s$), der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) kann ein Charakteristische Länge der Strömung im Boden ($s_0$) wie folgt definiert werden:
| $ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$ |
Um die Analyse nicht zu komplizieren, haben wir die Ausdrucksweise unter Berücksichtigung des Betrags von der Strömung an einem Referenzpunkt ($j_{s0}$) definiert, um Situationen zu vermeiden, in denen dieser negativ ist. Dies bedeutet, dass je nach Vorzeichen von der Strömung an einem Referenzpunkt ($j_{s0}$) die Beziehung unter Annahme einer positiven oder negativen Ableitung ausgedrückt werden muss, was die Flussrichtung definiert.
ID:(4747, 0)
Fließgleichung in einen Kanal
Gleichung
Die Differentialgleichung zur Berechnung von die Höhe der Wassersäule am Boden ($h$) als Funktion von die Position der Wassersäule am Boden ($x$), die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) lautet:
| $ h \displaystyle\frac{ dh }{ dx } = \displaystyle\frac{ h_0 ^2 }{ s_0 } $ |
Die Gleichung für das Produkt von die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) als Funktion von die Referenzhöhe der Wassersäule ($h_0$) und der Strömung an einem Referenzpunkt ($j_{s0}$) lautet:
| $ h j_s = h_0 j_{s0} $ |
Und mit der Gleichung, die die Flussdichte ($j_s$) in Bezug auf die Hydraulische Leitfähigkeit ($K_s$) und die Position der Wassersäule am Boden ($x$) beschreibt:
| $$ |
Und mit dem Ausdruck für der Charakteristische Länge der Strömung im Boden ($s_0$):
| $ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$ |
Können wir die resultierende Gleichung wie folgt ableiten:
| $ h \displaystyle\frac{ dh }{ dx } = \displaystyle\frac{ h_0 ^2 }{ s_0 } $ |
ID:(15108, 0)
Fließhöhe in einen Kanal
Gleichung
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) als Funktion von der Charakteristische Länge der Strömung im Boden ($s_0$) und abhängig von die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) lautet wie folgt:
| $ h \displaystyle\frac{ dh }{ dx } = \displaystyle\frac{ h_0 ^2 }{ s_0 } $ |
Diese Gleichung kann für die gegebenen Bedingungen mit die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) an der Kanalgrenze analytisch gelöst werden, wie folgt:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $ |
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) als Funktion von der Charakteristische Länge der Strömung im Boden ($s_0$) und abhängig von die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) lautet wie folgt:
| $ h \displaystyle\frac{ dh }{ dx } = \displaystyle\frac{ h_0 ^2 }{ s_0 } $ |
Wir können sie umstellen, um die Integration zu erleichtern, wie folgt:
$h dh = \displaystyle\frac{h_0^2}{x_0}dx$
Dann, indem wir bezüglich von $h_0$, der Höhe am Ursprung, integrieren, erhalten wir:
$\displaystyle\frac{1}{2}(h^2 - h_0^2) =\displaystyle\frac{h_0^2}{s_0}x$
Dies führt uns zu folgendem Ausdruck:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $ |
ID:(15105, 0)
Strömungsdichte im Fluß zum Kanal
Gleichung
Die Flussdichte ($j_s$) ist in Beziehung zu die Hydraulische Leitfähigkeit ($K_s$), die Höhe der Wassersäule am Boden ($h$) und die Position der Wassersäule am Boden ($x$), was zu
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
führt. Daher erhalten wir mit der Lösung für die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) bei gegebenem die Position der Wassersäule am Boden ($x$) und der Charakteristische Länge der Strömung im Boden ($s_0$):
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Mit der Lösung für die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) bei gegebenem die Position der Wassersäule am Boden ($x$) und der Charakteristische Länge der Strömung im Boden ($s_0$) erhalten wir:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $ |
Wir können die Flussdichte ($j_s$) mit die Hydraulische Leitfähigkeit ($K_s$) berechnen, indem wir verwenden:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
und unter Verwendung von
| $ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$ |
erhalten wir auf diese Weise:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }}} $ |
ID:(15106, 0)
Strömungsgleichung aus einem Kanal
Gleichung
Die Differentialgleichung zur Berechnung von die Höhe der Wassersäule am Boden ($h$) in Abhängigkeit von die Position der Wassersäule am Boden ($x$), die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) lautet wie folgt:
| $ h \displaystyle\frac{ dh }{ dx } = -\displaystyle\frac{ h_0 ^2 }{ x_0 } $ |
In diesem Fall ist das Vorzeichen der Steigung negativ, da die Höhe abnehmen muss, um den erforderlichen Druckgradienten für die Bewegung der Flüssigkeit zu erzeugen.
ID:(4369, 0)
Fließhöhe aus einem Kanal
Gleichung
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) als Funktion von der Charakteristische Länge der Strömung im Boden ($s_0$), die von die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) abhängt, lautet wie folgt:
| $ h \displaystyle\frac{ dh }{ dx } = -\displaystyle\frac{ h_0 ^2 }{ x_0 } $ |
Diese Gleichung kann für die gegebenen Bedingungen mit die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) am Rande des Kanals auf analytischem Wege wie folgt gelöst werden:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }} $ |
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) als Funktion von der Charakteristische Länge der Strömung im Boden ($s_0$), die von die Referenzhöhe der Wassersäule ($h_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) abhängt, lautet wie folgt:
| $ h \displaystyle\frac{ dh }{ dx } = -\displaystyle\frac{ h_0 ^2 }{ x_0 } $ |
Wir können sie umstellen, um die Integration zu erleichtern, wie folgt:
$h dh = -\displaystyle\frac{h_0^2}{x_0}dx$
Dann, indem wir mit Bezug auf $h_0$, die Höhe am Ursprung, integrieren, erhalten wir:
$\displaystyle\frac{1}{2}(h^2 - h_0^2) =-\displaystyle\frac{h_0^2}{x_0}x$
Dies führt uns zu folgendem Ausdruck:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }} $ |
ID:(2214, 0)
Strömungsdichte aus einem Kanal
Gleichung
Die Flussdichte ($j_s$) steht in Beziehung zu die Hydraulische Leitfähigkeit ($K_s$), die Höhe der Wassersäule am Boden ($h$) und die Position der Wassersäule am Boden ($x$), was zu folgendem Ergebnis führt:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Daher erhalten wir mit der Lösung für die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) bei gegebenem die Position der Wassersäule am Boden ($x$) und der Charakteristische Länge der Strömung im Boden ($s_0$):
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }}} $ |
Mit der Lösung für die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) bei gegebenem die Position der Wassersäule am Boden ($x$) und der Charakteristische Länge der Strömung im Boden ($s_0$) erhalten wir:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }} $ |
Wir können die Flussdichte ($j_s$) mit die Hydraulische Leitfähigkeit ($K_s$) berechnen, indem wir verwenden:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
und unter Verwendung von
| $ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$ |
auf diese Weise erhalten wir:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ x_0 }}} $ |
ID:(4742, 0)
Statische Lösung in mehr als einer Dimension
Gleichung
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) mit der Zeit ($t$) und die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$) lautet:
| $\displaystyle\frac{\partial h}{\partial t} = - \vec{\nabla} \cdot ( h \vec{j}_s )$ |
Im stationären Fall und unter Verwendung der Gleichung für die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$), wenn wir die Ableitungen entwickeln, erhalten wir:
| $ h \nabla^2 h + \nabla h \cdot \nabla h = 0 $ |
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) mit der Zeit ($t$) und die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$) lautet:
| $\displaystyle\frac{\partial h}{\partial t} = - \vec{\nabla} \cdot ( h \vec{j}_s )$ |
in Bezug auf
| $ \vec{j}_s = - K_s \nabla h $ |
ergibt sich nach dem Ersetzen und Entwickeln der Ableitung
$\displaystyle\frac{\partial h}{\partial t}=-\vec{\nabla}\cdot(h\vec{j}_s)= K_s\vec{\nabla}\cdot(h\nabla h)=K_s(\vec{\nabla} h\cdot\vec{\nabla} h + h \nabla^2 h)$
was im stationären Fall auf
| $ h \nabla^2 h + \nabla h \cdot \nabla h = 0 $ |
hinausläuft.
ID:(4375, 0)
Gleichung für den Zufluss in einen Brunnen
Gleichung
Im Fall des Brunnens können wir mit einem Polarkoordinatensystem arbeiten und eine winkelsymmetrische Annahme treffen, was bedeutet, dass die Höhe der Wassersäule am Boden ($h$) nur von der Radius von der Mitte des Bohrlochs ($r$) abhängt und die Gleichung erfüllt
| $ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $ |
Da die Höhe der Wassersäule am Boden ($h$) die Gleichung
| $ h \nabla^2 h + \nabla h \cdot \nabla h = 0 $ |
erfüllt und in Polarkoordinaten mit der Radius von der Mitte des Bohrlochs ($r$) für den Fall der Winkelsymmetrie haben wir
$\vec{\nabla}h = \displaystyle\frac{du}{dr}\hat{r}$
und
$\nabla ^2h = \displaystyle\frac{1}{r}\displaystyle\frac{d}{dr}\left(r\displaystyle\frac{dh}{dr}\right)$
erhalten wir
$\displaystyle\frac{1}{r}\displaystyle\frac{d}{dr}\left(r\displaystyle\frac{dh^2}{dr}\right)=0$
oder
$r\displaystyle\frac{dh^2}{dr}=C$
mit $C$ als Konstante. Andererseits reduziert sich die Gleichung mit die Hydraulische Leitfähigkeit ($K_s$) und die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$)
| $ \vec{j}_s = - K_s \nabla h $ |
in Polarkoordinaten mit Rotationssymmetrie auf
$j_s = - K_s \displaystyle\frac{dh}{dr}$
was an der Oberfläche des Brunnens mit der Brunnenradius ($r_0$), der Charakteristische Länge der Strömung im Boden ($s_0$), der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) dazu führt, dass mit
| $ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$ |
wir haben
$C=r_0\displaystyle\frac{dh^2}{dr}=r_02h_0\displaystyle\frac{dh}{dr}=2r_0h_0\displaystyle\frac{|j_{s0}|}{K_sh_0}=2h_0^2\displaystyle\frac{r_0}{s_0}$
was zu
| $ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $ |
führt.
ID:(4430, 0)
Höhe des Zuflusses in einen Brunnen
Gleichung
Im Fall des Flusses in Richtung eines Brunnens wird die Höhe der Wassersäule am Boden ($h$) als Funktion von der Radius von der Mitte des Bohrlochs ($r$) mit der Brunnenradius ($r_0$), der Charakteristische Länge der Strömung im Boden ($s_0$) und die Referenzhöhe der Wassersäule ($h_0$) repräsentiert durch
| $ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $ |
Diese Gleichung kann analytisch für die gegebenen Bedingungen gelöst werden, wenn der Brunnenradius ($r_0$) und die Referenzhöhe der Wassersäule ($h_0$) am Rand des Brunnens liegen, wie folgt:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) als Funktion von der Radius von der Mitte des Bohrlochs ($r$) mit der Brunnenradius ($r_0$), der Charakteristische Länge der Strömung im Boden ($s_0$) und die Referenzhöhe der Wassersäule ($h_0$) lautet wie folgt:
| $ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $ |
Diese Gleichung kann umgeformt werden, um die Integration zu erleichtern, wie folgt:
$dh^2 = 2h_0^2\displaystyle\frac{r_0}{s_0}\displaystyle\frac{dr}{r}$
Anschließend, durch Integration beider Seiten, erhalten wir die Höhe an der Wand des Brunnens mit die Referenzhöhe der Wassersäule ($h_0$) und der Brunnenradius ($r_0$):
$h^2 - h_0^2 = 2h_0^2\displaystyle\frac{r_0}{s_0}\ln\left(\displaystyle\frac{r}{r_0}\right)$
Schließlich, durch Umstellen von die Höhe der Wassersäule am Boden ($h$), erhalten wir:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
ID:(10593, 0)
Fließdichte in einen Brunnen
Gleichung
Die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$) ist mit die Hydraulische Leitfähigkeit ($K_s$) verwandt und in Polarkoordinaten mit einer Winkelsymmetrie von der Radius von der Mitte des Bohrlochs ($r$) ergibt sich
| $ \vec{j}_s = - K_s \nabla h $ |
Daher erhalten wir mit der Lösung für die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) bei gegebenem der Radius von der Mitte des Bohrlochs ($r$), der Brunnenradius ($r_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$):
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
Mit der Lösung für die Höhe der Wassersäule am Boden ($h$) und die Referenzhöhe der Wassersäule ($h_0$) unter Berücksichtigung von der Radius von der Mitte des Bohrlochs ($r$), der Brunnenradius ($r_0$) und der Charakteristische Länge der Strömung im Boden ($s_0$) erhalten wir:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
Wir können die Strömungsdichte in mehr als einer Dimension ($\vec{j}_s$) aus die Hydraulische Leitfähigkeit ($K_s$) wie folgt berechnen:
| $ \vec{j}_s = - K_s \nabla h $ |
Und mit die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) unter Verwendung von
| $ s_0 \equiv \displaystyle\frac{| j_{s0} |}{ K_s h_0 }$ |
auf diese Weise erhalten wir:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
ID:(4368, 0)