Storyboard

>Modèle

ID:(367, 0)

Définition

ID:(15205, 0)

Image

A densité de flux ($j_s$) peut être exprimé en termes de a conductivité hydraulique ($K_s$), dans la limite infinitésimale avec a différentiel de hauteur de colonne ($dh$) et a différentiel de distance ($dx$), comme suit :



Cela signifie que plus le gradient est raide ou plus le terrain est pentu, plus a densité de flux ($j_s$) sera grand, comme illustré dans le graphique :

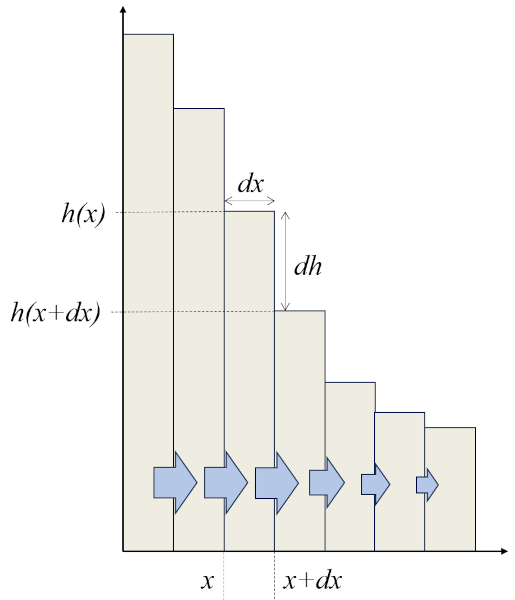
Le graphique montre comment les barres ayant des valeurs égales de ERROR:10142,0 ont progressivement des valeurs de ERROR:10141,0 de plus en plus petites, entraînant une diminution de ERROR:7220,0. Étant donné que le volume du liquide est conservé, cela ne peut être possible que s'il existe un autre flux qui compense cette réduction de ERROR:7220,0. Il pourrait s'agir d'un flux perpendiculaire à celui montré dans le graphique, par exemple, si les barres plus courtes sont plus larges dans une direction perpendiculaire au graphique.

Ce problème conduit aux considérations suivantes :

La hauteur $h$ du liquide ne peut être calculée qu'en résolvant une équation différentielle, car elle doit satisfaire à l'exigence que le volume soit conservé sur l'ensemble de la zone où s'écoule le fluide.

De plus, il est important de garder à l'esprit que :

Le signe négatif reflète le fait que le flux s'écoule toujours de la zone de plus haute altitude vers celle de plus basse altitude. Si la pente est négative, le signe négatif entraîne un flux positif (de gauche à droite), et inversement, si la pente est positive, le flux est négatif (de droite à gauche).

ID:(930, 0)

Noter

Si nous étudions le cas unidimensionnel, décrivant le processus le long de l'axe $x$, nous pouvons observer comment la hauteur de la colonne $\Delta h$ varie sur un intervalle de temps $\Delta t$. Dans ce cas, une colonne d'une largeur $\Delta x$ changera son volume par unité de longueur au fil du temps comme $\Delta x \Delta h/\Delta t$. D'autre part, la quantité de liquide qui entre le long de la colonne en $x$ est $h(x) j_s(x)$, tandis qu'en $x+\Delta x$ il en sort comme $h(x+\Delta x) j_s(x+\Delta x)$ :

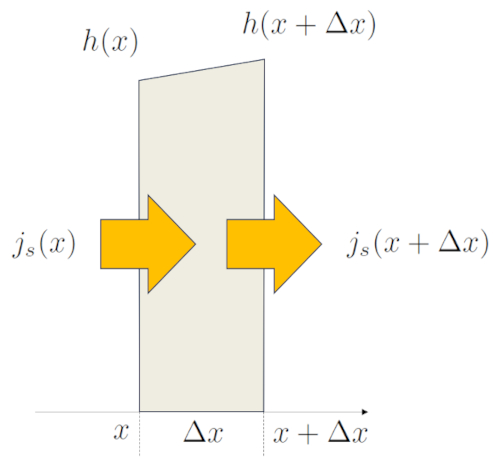
Par conséquent, la variation de a hauteur de la colonne d'eau au sol ($h$) au fil du temps est égale à la variation du produit de a hauteur de la colonne d'eau au sol ($h$) et a densité de flux ($j_s$) à la position :

Les dérivées partielles sont similaires aux dérivées ordinaires, à la différence qu'elles s'appliquent à des fonctions qui dépendent de plus d'une variable. Dans ces cas, la dérivée partielle, représentée par le symbole $\partial$, nous rappelle la dérivée classique notée par la lettre $d$, mais avec la particularité que les variables non mentionnées au dénominateur sont maintenues constantes.

ID:(2290, 0)

Citation

Dans le cas de l'écoulement vers un canal, le système peut être modélisé de manière unidimensionnelle, où A hauteur de la colonne d'eau au sol ($h$) est une fonction de a position de la colonne d'eau au sol ($x$) représentant a densité de flux ($j_s$), et elle satisfait à la condition



avec le flux à un point de référence ($j_{s0}$) et a hauteur de référence de la colonne d'eau ($h_0$) définissant le profil de l'eau dans le sol :

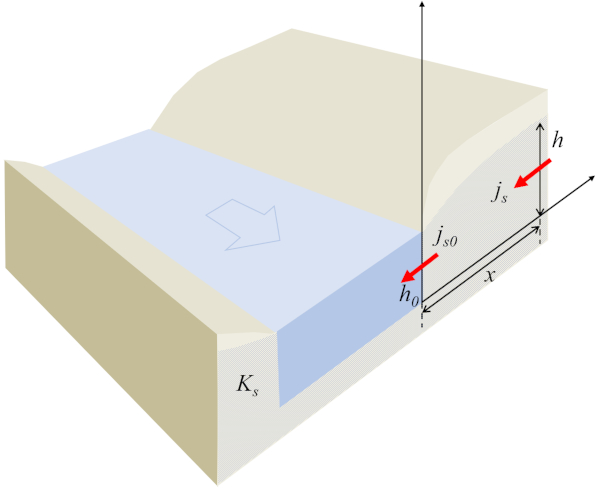
La clé de cette équation est que le produit de a hauteur de la colonne d'eau au sol ($h$) et de a densité de flux ($j_s$) doit toujours rester constant. En ce sens, si a hauteur de la colonne d'eau au sol ($h$) augmente, a densité de flux ($j_s$) diminue et vice versa. De plus, le signe reste le même ; donc, l'écoulement vers le canal, c'est-à-dire l'écoulement négatif, se produira uniquement lorsque le niveau de la nappe phréatique est plus élevé que celui du canal. À mesure que le liquide s'approche du canal, le niveau de la nappe phréatique diminue, entraînant une augmentation de la densité de l'écoulement.

ID:(15104, 0)

Exercer

La solution de l'équation de flux unidimensionnel en direction d'un canal, où A hauteur de la colonne d'eau au sol ($h$) est calculé en fonction de a hauteur de référence de la colonne d'eau ($h_0$) et a position de la colonne d'eau au sol ($x$) au bord du canal, ainsi que de le longueur caractéristique de l'écoulement dans le sol ($s_0$), a la forme suivante :



Cette solution est représentée graphiquement en fonction des facteurs supplémentaires $h/h_0$ et $x/s_0$ de la manière suivante :

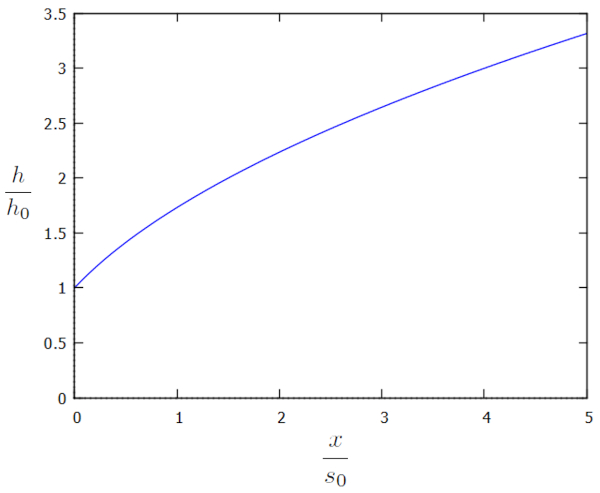
Le profil révèle qu'à distance du canal, la hauteur de la colonne d'eau est considérablement élevée. Cependant, en raison de l'extraction d'eau par le canal, cette hauteur commence à diminuer jusqu'à atteindre le bord du canal. Dynamiquement, a densité de flux ($j_s$) détermine la quantité d'eau qui s'écoule dans le canal, tandis que a hauteur de référence de la colonne d'eau ($h_0$) s'ajuste progressivement jusqu'à atteindre un état d'équilibre. En d'autres termes, si la valeur de a hauteur de référence de la colonne d'eau ($h_0$) est trop basse par rapport à la quantité totale d'eau qui arrive dans le canal, elle augmente ; et si elle est trop élevée, elle diminue. De cette manière, a hauteur de référence de la colonne d'eau ($h_0$) acquiert la valeur qui équilibre la quantité d'eau entrante avec la quantité d'eau s'écoulant à travers le canal.

ID:(15109, 0)

Équation

La solution obtenue pour la hauteur et les paramètres le flux à un point de référence ($j_{s0}$) et a hauteur de référence de la colonne d'eau ($h_0$) révèle que a densité de flux ($j_s$) est donné par :



Nous pouvons représenter graphiquement a densité de flux ($j_s$) en fonction des facteurs additionnels $j_s/j_{s0}$ et $x/s_0$ de la manière suivante :

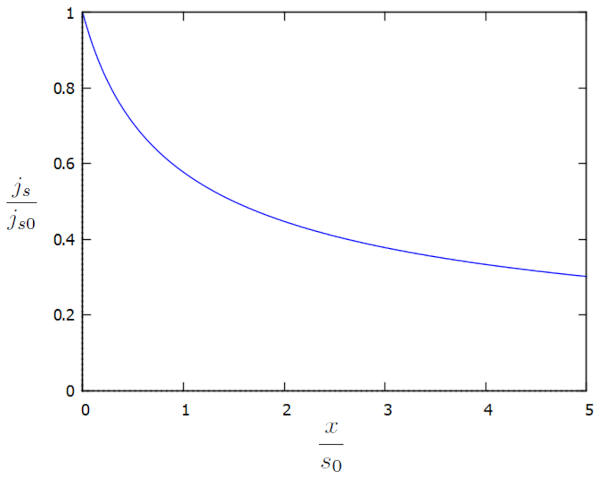
Il est notable que a densité de flux ($j_s$) continue d'augmenter à mesure que nous nous approchons du canal, car a hauteur de la colonne d'eau au sol ($h$) diminue. Cette augmentation est nécessaire pour maintenir la vitesse de l'écoulement dans a densité de flux ($j_s$) ou, en alternance, pour l'augmenter.

ID:(15110, 0)

Script

Dans le cas où le flux émerge du canal, une situation se présente où le niveau de a hauteur de la colonne d'eau au sol ($h$) doit diminuer à mesure que l'on s'éloigne du canal, assurant ainsi l'existence du gradient de pression qui entraîne le flux. Le problème est que si le flux se déplace rapidement à l'intérieur du milieu, la hauteur aura tendance à atteindre zéro et, par conséquent, le flux approchera l'infini, ce qui n'a aucun sens.

Cela signifie qu'il n'y a pas de solution stationnaire dans un tel scénario, et la seule solution est que le milieu se remplisse jusqu'à atteindre la hauteur du canal, devenant ainsi effectivement constant.

La question est de savoir s'il existe une situation stationnaire non triviale qui représente une situation réelle et intéressante. Un cas possible est lorsque le niveau du milieu diminue au point de devenir plus bas que la colonne avant que la solution ne diverge. Ce cas correspond à la situation où le flux émerge à la surface, et il n'y a pas de divergence dans la solution. Cela impliquerait qu'un flux est généré et sort à l'extérieur à un certain point, avec le risque d'affaiblir les fondations et ainsi de déstabiliser le milieu, qui agit comme un barrage.

ID:(4746, 0)

Variable

Si nous considérons une situation où le flux du canal peut émerger à la surface, nous avons une situation où le flux pénètre puis sort du milieu, rendant la solution viable.

L'émergence à la surface implique simplement que la hauteur de la colonne de liquide devient plus élevée que celle du milieu environnant. En fait, de manière similaire au cas du flux vers un canal, cela générerait de l'eau en surface, qui, si elle n'est pas autorisée à s'écouler, formerait effectivement un nouveau canal.

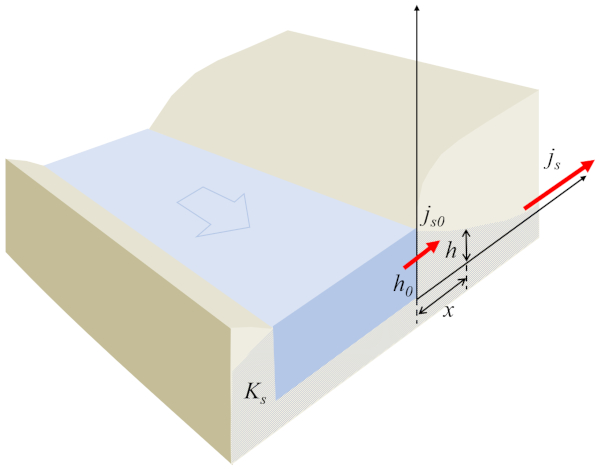
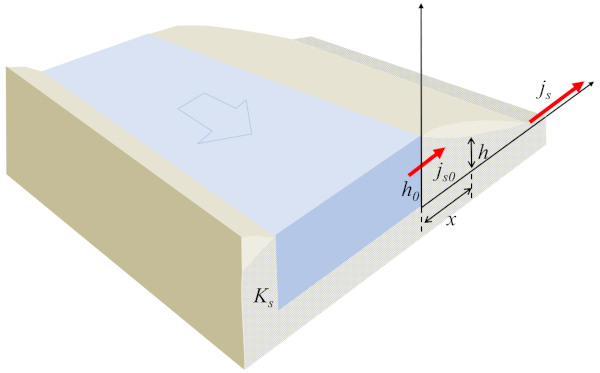
Dans le cas du flux provenant d'un canal, il est possible de modéliser le système de manière unidimensionnelle, où A hauteur de la colonne d'eau au sol ($h$) est une fonction de a position de la colonne d'eau au sol ($x$) représentant a densité de flux ($j_s$) et satisfaisant à la condition suivante :



Avec le flux à un point de référence ($j_{s0}$) et a hauteur de référence de la colonne d'eau ($h_0$) définissant le profil de l'eau dans le sol, comme indiqué dans l'image suivante :

La clé de l'équation réside dans le fait que le produit de a hauteur de la colonne d'eau au sol ($h$) et a densité de flux ($j_s$) doit rester constant en tout temps. Dans ce sens, si a hauteur de la colonne d'eau au sol ($h$) augmente, a densité de flux ($j_s$) diminuera, et vice versa. De plus, le signe reste le même. Par conséquent, le flux du canal, c'est-à-dire le flux positif, ne se produira que si la hauteur du canal est supérieure à celle du point où le flux émerge. À mesure que le liquide s'éloigne du canal, la hauteur diminuera, et la densité du flux augmentera.

ID:(4370, 0)

Audio

La solution de l'équation de flux unidimensionnel depuis un canal, dans laquelle la valeur de a hauteur de la colonne d'eau au sol ($h$) est calculée en fonction de a hauteur de référence de la colonne d'eau ($h_0$) et a position de la colonne d'eau au sol ($x$) au bord du canal, ainsi qu'avec le longueur caractéristique de l'écoulement dans le sol ($s_0$), prend la forme suivante :



Cette solution est représentée graphiquement en fonction des facteurs supplémentaires $h/h_0$ et $x/x_0$ de la manière suivante :

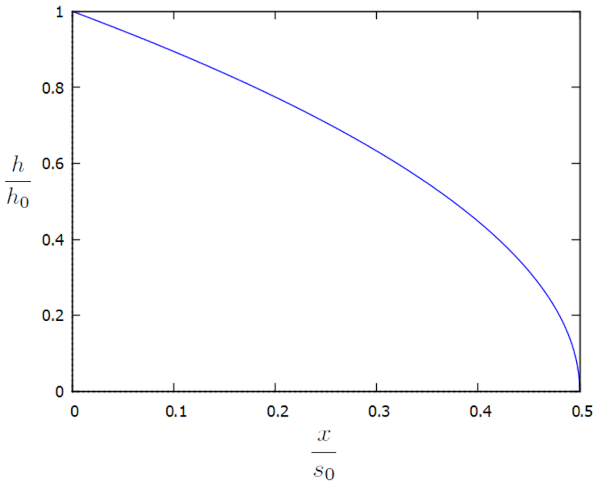
Le profil révèle que la hauteur diminue à mesure que l'on s'éloigne du canal pour maintenir un gradient de pression. Cependant, un problème survient lorsque la distance atteint la moitié de le longueur caractéristique de l'écoulement dans le sol ($s_0$), car la hauteur de la colonne atteint zéro et il n'y a pas de solution pour des distances plus grandes (l'argument de la racine carrée devient négatif). En d'autres termes, pour que la solution ait un sens, il doit y avoir un mécanisme qui élimine le liquide avant d'atteindre cette distance critique.

ID:(4374, 0)

Video

La solution obtenue pour la hauteur et les paramètres le flux à un point de référence ($j_{s0}$) et a hauteur de référence de la colonne d'eau ($h_0$) nous montre que a densité de flux ($j_s$) est égal à :



Nous pouvons représenter graphiquement a densité de flux ($j_s$) en fonction des facteurs additionnels $j_s/j_{s0}$ et $x/x_0$ comme suit :

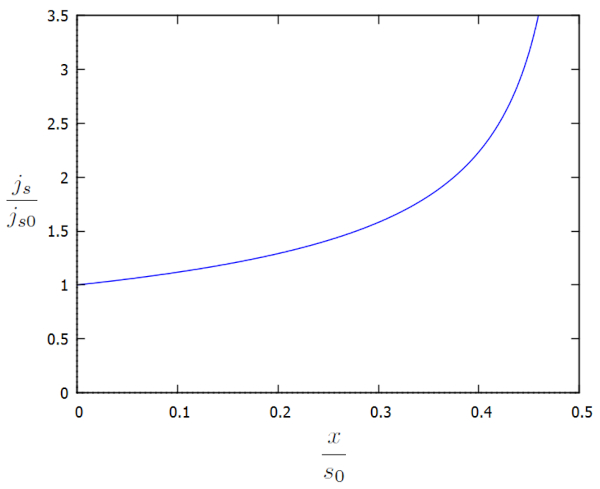
a densité de flux ($j_s$) continue d'augmenter à mesure que nous nous approchons du canal, tandis que a hauteur de la colonne d'eau au sol ($h$) diminue. Cette augmentation est nécessaire pour maintenir la vitesse d'écoulement dans a densité de flux ($j_s$) ou, en alternative, pour l'augmenter.

ID:(7827, 0)

Unité

Un exemple illustrant l'effet du flux à travers la base dans le cas d'un barrage est survenu au Barrage 1 de la mine 'Córrego do Feijão' à Brumadinho, Minas Gerais, au Brésil.

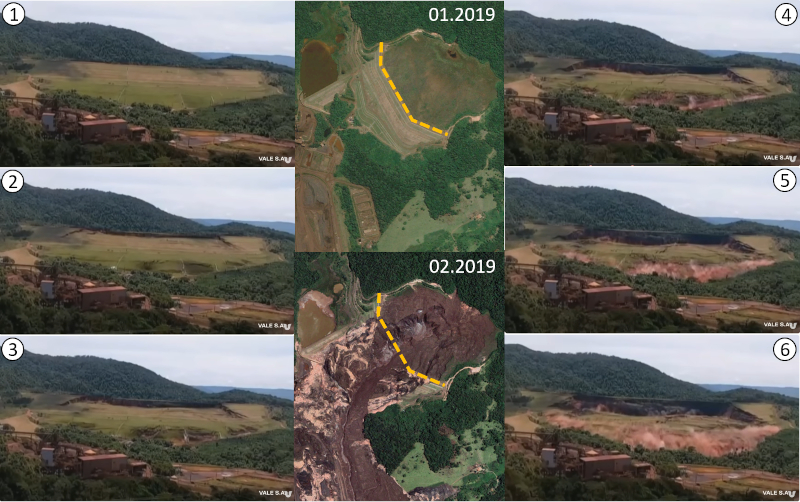
Le 25 janvier 2019, le Barrage 1, qui se trouve au centre de l'image, s'est effondré comme le montrent les images de 1 à 6. Initialement, la base a commencé à se déplacer tandis que le sommet a commencé à s'enfoncer. Finalement, un torrent d'eau a émergé de la base alors que toute la structure s'effondrait. Sur l'image centrale inférieure, vous pouvez voir la situation après que le barrage se soit complètement vidé du côté qui le contenait ([1], [2]) :

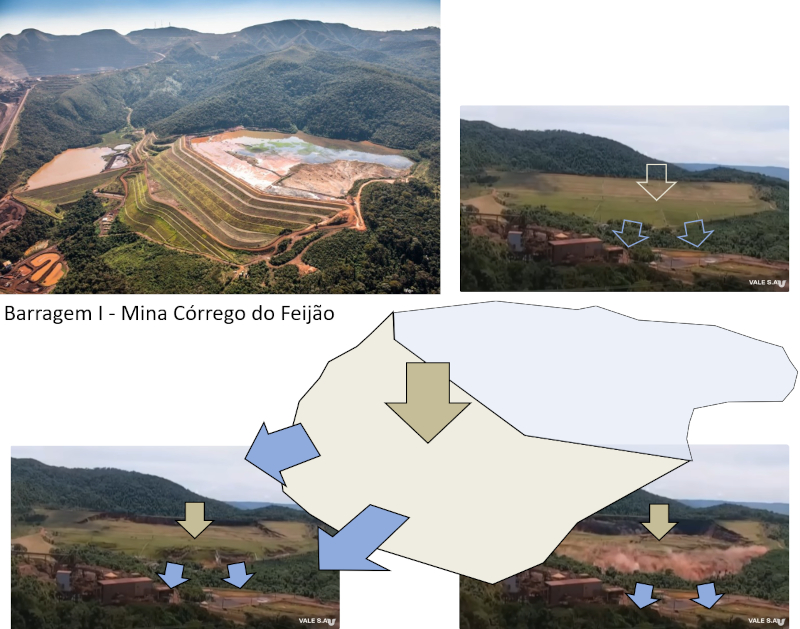
L'image en haut à gauche montre le barrage avant l'effondrement, et le schéma explique comment l'eau pousse contre la surface de la base (flèches bleues) et fait s'effondrer le centre (flèche beige). Les images montrent à nouveau la structure avant l'effondrement (photo en haut à droite), lorsque la base est forcée, provoquant l'effondrement de la partie supérieure (photo en bas à gauche), et le débit d'eau résultant à la base (photo en bas à droite) [3] :

La dynamique est générée par la forte pression et le débit élevé qui existent à la base, expliquant l'émergence de l'eau par ce chemin.

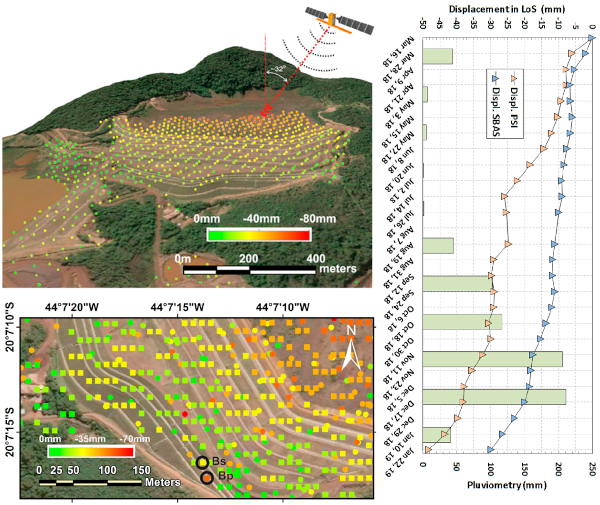
Dans ce cas, il y avait de multiples signes de danger, ce qui a conduit à une surveillance satellite détaillée du mouvement de plusieurs points pendant plus d'un an. Les points sont indiqués sur la photo supérieure, et sur la deuxième image en bas à gauche, vous pouvez voir un détail de la base. Plus précisément, les points qui ont connu le plus grand déplacement total (Bs et Bp) sont mis en évidence, et ces points sont également représentés sur le graphique à droite. Le graphique montre également la quantité de pluie, qui contribue dans une certaine mesure mais n'est pas nécessairement un facteur clé [4] :

Cet exemple vise à démontrer comment une forte pression à la base, associée à un débit d'eau élevé, contribue à la dynamique observée, sans nécessairement expliquer quand ou comment elle est devenue instable. Cela sera exploré plus en détail par la suite.

[1] Google Earth Pro pour Brumadinho, Minas Gerais, Brésil, janvier 2019 et février 2019

[2] Caméras de la Vale S.A.

[3] Procédure d'Investigation Criminelle n° MPMG-0090.19.000013-4, Enquête de Police n° PCMG-7977979, MINISTÉRIO PÚBLICO DO ESTADO DE MINAS GERAIS

[4] Déformations Précédant l'Effondrement du Barrage de Brumadinho Révélées par des Données InSAR du Sentinel-1 Utilisant les Techniques SBAS et PSI, Fábio F. Gama, José C. Mura, Waldir R. Paradella et Cleber G. de Oliveira, MDPI, Remote Sens. 2020, 12, 3664.

ID:(4378, 0)

Code

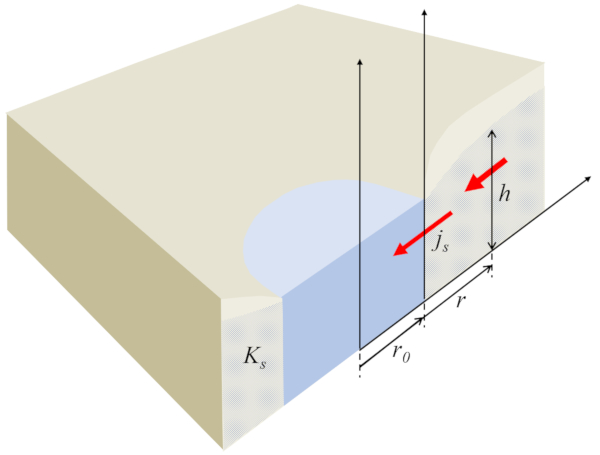
Dans le cas de l'écoulement de l'eau souterraine vers un puits, a hauteur de la colonne d'eau au sol ($h$) en fonction de le rayon du centre du puits ($r$) avec le rayon du puits d'eau ($r_0$), le longueur caractéristique de l'écoulement dans le sol ($s_0$) et a hauteur de référence de la colonne d'eau ($h_0$) est représenté par



ce qui définit le profil de l'eau dans le sol :

ID:(4371, 0)

Flux

La solution de l'équation de flux unidimensionnel en direction d'un puits, dans laquelle la valeur de a hauteur de la colonne d'eau au sol ($h$) est calculée en fonction de le rayon du centre du puits ($r$), a hauteur de référence de la colonne d'eau ($h_0$) et le rayon du puits d'eau ($r_0$) au bord du puits, ainsi que le longueur caractéristique de l'écoulement dans le sol ($s_0$), a la forme suivante :



Cette solution est représentée graphiquement en fonction des facteurs supplémentaires $h/h_0$ et $r/r_0$ pour différentes valeurs de $r_0/s_0$, comme suit :

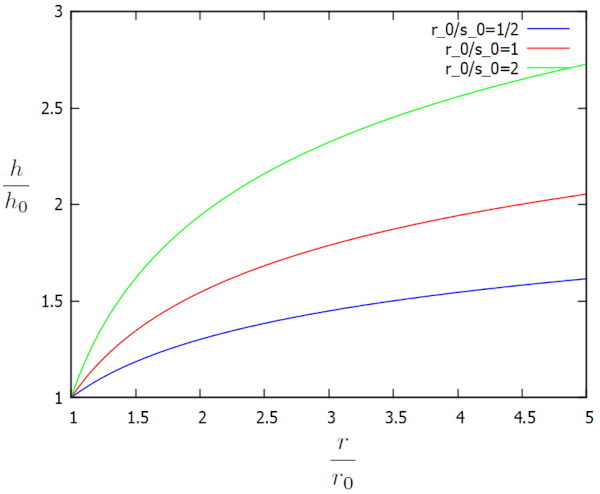
Le profil révèle que, loin du puits, la hauteur de la colonne d'eau est nettement élevée. Cependant, en raison de l'extraction d'eau par le puits, cette hauteur commence à diminuer jusqu'à atteindre le bord du puits. Dynamiquement, a densité de flux ($j_s$) détermine la quantité d'eau qui s'écoule vers le puits, tandis que a hauteur de référence de la colonne d'eau ($h_0$) s'ajuste progressivement pour atteindre un état d'équilibre. En d'autres termes, si la valeur de a hauteur de référence de la colonne d'eau ($h_0$) est trop faible par rapport à la quantité totale d'eau qui arrive au puits, elle augmente, et si elle est trop élevée, elle diminue. Ainsi, a hauteur de référence de la colonne d'eau ($h_0$) acquiert la valeur qui équilibre la quantité d'eau qui arrive avec la quantité d'eau qui est extraite par le puits.

ID:(10591, 0)

Matrice

La solution obtenue pour la hauteur et les paramètres le flux à un point de référence ($j_{s0}$) et le rayon du centre du puits ($r$), le rayon du puits d'eau ($r_0$), le longueur caractéristique de l'écoulement dans le sol ($s_0$) nous montre que a densité de flux ($j_s$) est égal à :



Cette solution est représentée graphiquement en fonction des facteurs supplémentaires $j_s/j_{s0}$ et $r/r_0$ pour diverses valeurs de $r_0/s_0$ de la manière suivante :

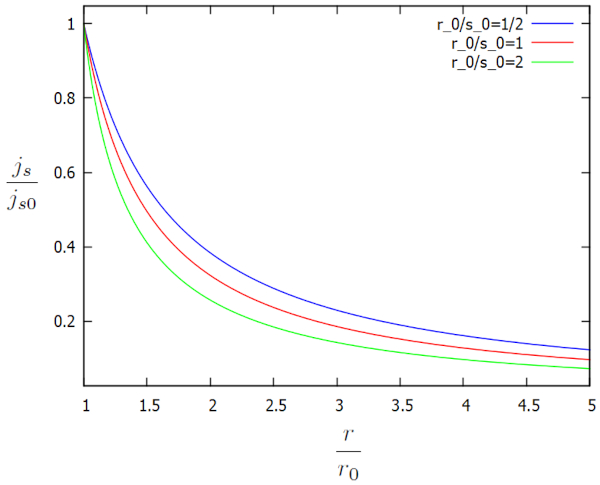
a densité de flux ($j_s$) continue d'augmenter à mesure que nous nous approchons du canal, tandis que a hauteur de la colonne d'eau au sol ($h$) diminue. Cette augmentation est nécessaire pour maintenir la vitesse de l'écoulement dans a densité de flux ($j_s$) ou, en alternative, pour l'augmenter.

ID:(2209, 0)

Html

ID:(15224, 0)